基于遗传算法解决二维连续型无约束优化问题

说来惭愧，之前没有接触过优化类问题，但是这学期却学了《工程优化》《计算智能》《自然计算》三门关于优化的科目，其中计算智能和自然计算中老师都着重讲解了遗传算法。本次博客是我大作业的一部分，为以后有需要的同学或者了解其算法但不知道怎样实现的新手参考下。

代码是根据个人理解原创的，下面就代码和思路进行说明。其中代码风格是面向过程风格，使用编程语言是Python。另外，个人水平有限，如有错误，欢迎指出。

遗传算法是一种借鉴生物界适者生存，优胜劣汰遗传机制演化而来的随机搜索方法。
其原理见下图

算法的结构包括染色体编码，种群初始化，适应度评价，选择算子，交叉算子，变异算子。

关于基础的讲解其中一片博客https://blog.csdn.net/u010451580/article/details/51178225讲解的很清楚。

初始化种群

染色体编码，将浮点数或者整数转换成二进制。其中浮点数先确定精度，转换为整数，在转换成二进制。（举个例子，2.51精度精确到小数点5位，2.51*(10 ** 5)）<2**L -1 确定L即为串长。由于二维问题，将两个长度长度叠加在一起就是种群个体染色体的长度。

初始化种群的时候，我想到需要数据种群的数目和种群的长度，以及最后输出种群。
其中初始化种群函数如下所示。

def Init_bin(num,len,animal_population):
    """初始化，生成种群"""
    tmp_len = len
    tmp_num = 0
    print("二进制编码")
    
    if num <= 0:
        print("输入的数量不正确，没有生成种群\n")
        return
    if len <= 0:
        print("输入的长度不正确，没有生成染色体\n")
        return
        
    while tmp_num

适应度评价

适应度评价是将初始化的种群个体解码，然后带入到适应度函数中，得到目标函数的值。

解码的时候，考虑到对每一个个体进行编码封装成函数。其中函数参数为染色体的长度len，初始化时讲二维变量叠加在一起的中间节点mid_node,变量1的最小值、最大值，变量2的最小值、最大值，编码空间，输入的编码个体code_indivi，存储解码后2个变量的列表cur_indivi。

个体解码

def Decode_Indivi_twodemi_bin(len,mid_node,min1,max1,min2,max2,code_indivi,cur_indivi):
    """对每个个体进行解码"""
    if mid_node > len:
        print("不符合解码规则，一变量所占的长度超过总的长度")
        return
        
    tmp_num2 = int(code_indivi,2)%(2**mid_node)				#获取变量2的二进制
    tmp_num2 = min2+(tmp_num2*(max2-min2))/(2**mid_node-1)	#得到变量2的int型

    tmp_num1 = (int(code_indivi, 2) - tmp_num2)/(2**mid_node)#获取变量1的二进制
    tmp_num1 = min1+(tmp_num1*(max1-min1))/(2**(len-mid_node)-1)#得到变量1的int型

    cur_indivi.append(tmp_num1)
    cur_indivi.append(tmp_num2)

    return cur_indivi

种群解码
种群解码是针对种群中的每一个个体进行解码，实现种群解码操作。

在个体解码需要的输入参数上增加了种群数目num,编码种群animal_population，解码种群curanimal_population1

#种群进行解码
def Decode_Population_bin(num,animal_population,curanimal_population1,indiv_len,mid_node,min1,max1,min2,max2):
    """运用个体解码，实现种群解码"""
    for i in range(num):
        curanimal_population1.append(Decode_Indivi_twodemi_bin(indiv_len,mid_node,min1,max1,min2,max2,animal_population[i],curanimal_population1))
        curanimal_population1.pop() #如果不消除栈的话，每次都会多一个[]

代入适应度函数
将解码空间中的解代入适应度函数，得到目标函数值。这里需要注意的是：在遗传算法中适应度函数与选择算子息息相关，选择算子用的是轮盘赌选择(轮盘赌选择解决最大值问题)，如果你的目标函数是最小值问题，将函数取反或者取倒数，就变成了最小化问题。为了最后方便明确的表示，这里讲最优的解保存下来。

函数参数为解空间列表cur_population,适应度函数func（这里适应度函数为一个函数，我将函数的函数名传入，其根本是传入函数的首地址），目标函数值列表backeval。

注意：我在这个地方，选择目标函数值的时候出现过困扰，思路没有理清楚，考试复习的时候才搞清楚，并加以修改。

def Result_Population_bin_1(cur_population,func,backeval):
    """代入适应度函数，获得相对最优解"""
    for i in range(int(len(cur_population)/2)):
        backeval1 = func(cur_population[2*i],cur_population[2*i+1])  #得到目标函数值
        backeval.append(backeval1)									 
    #return backeval
    
    tmp = backeval[0]						#获取最大值的目标函数
    for j in range(len(backeval)):
        if tmp > backeval[j]:
            tmp = backeval[j]
            #print(backeval1[j])
    return tmp

选择算子

适应度函数评价上面提到了轮盘赌选择，轮盘赌选择是根据得到的目标函数值得到解个概率列表，求出累计概率分布，用随机生成的随机数查看落在什么区间，进而决定选择那个解。

累计概率

根据目标函数值的大小，获得每个解的概率，然后再得到累计概率。其中result_population为目标函数值列表，rata_population为累计概率列表。

def Rata_Population(result_population,rata_population):
    """得到概率列表"""
    tmp_total = 0
    every_rata = 0
    for i in range(len(result_population)):
        tmp_total += result_population[i]
    #print('总共的 解集是',tmp_total)
    for j in range(len(result_population)):
        every_rata += result_population[j]/tmp_total
        rata_population.append(every_rata)

轮盘赌选择
生成一个随机数，查看随机数所在累计概率区间的那个区间内，取区间的上界所在的个体。需要注意的是轮盘赌选择是根据解码个体代入适应度函数之后得到的目标函数值确定的，但是最后输出的结果是编码的个体。
轮盘赌选择的代码

def RoulettWheel(rata_population,select_population,animal_population):
    """得到选择列表"""
    tmp_random = 0.0
    for i in range(len(rata_population)):
        tmp_random = np.random.random()
        for j in range(len(rata_population)):  #遍历累计概率
            if j == 0:                         #第一个选择的元素，需要与0进行比较这是区别于其他元素的原因  #因为0-1= -1不符合列表内容
                if 0 < tmp_random and tmp_random <=rata_population[j]:	 
                    select_population.append(animal_population[j])
            else:
                if rata_population[j-1]

交叉算子

这里使用的是最简单的单点交叉，对于每一个种群个体来说，使用一个0-1的随机数来判断个体是否需要交叉，再根据一个0-染色体长度随机数判断个体那个部分与下一个个体进行交叉。所谓的交叉就是生成的染色体上，其中一个染色体前半段是我的基因，后半段是下一个个体的基因；另外一个是染色体前半段是后一个个体的基因，后半段是我的基因，从而实现了交叉运算。

输入参数为编码的种群select_population,交叉算子参数pc
其中代码为

def Crossover(select_population,pc):
    """交叉算子"""
    select_populationlen = len(select_population)
    for i in range(select_populationlen-1):  #两个才能进行交叉变异，所以循环到倒数第二位
        if (np.random.random() < pc):
            cpoint = np.random.randint(0,len(select_population[0]))  #产生一个随机数，用于确定交叉的位置
            tmp1 = []
            tmp2 = []
            tmp1.extend(select_population[i][0:cpoint])            #将i元素的前半段，加上i+1元素的后半段完成
            tmp1.extend(select_population[i+1][cpoint:select_populationlen])

            tmp2.extend(select_population[i+1][0:cpoint])
            tmp2.extend(select_population[i][cpoint:select_populationlen])

            tmp3 = ''.join(tmp1)
            tmp4 = ''.join(tmp2)
            select_population[i] = tmp3
            select_population[i+1] = tmp4

变异算子

变异运算是针对二进制编码最简单的单点变异。对于每一个种群个体来说，使用一个0-1的随机数来判断个体是否需要变异，再根据一个0-染色体长度随机数判断哪一位进行变异。如果基因为0则变为1，如果为1则变为0.

def  Mutation(select_population,pm):
    """变异算子"""
    for i in range(len(select_population)):
        if(np.random.random() < pm):
            tmp = list(select_population[i])
            mpoint = np.random.randint(0,len(select_population[i]))
            if tmp[mpoint] == '0':
                tmp[mpoint] = '1'
            else:
                tmp[mpoint] = '0'
            select_population[i] = ''.join(tmp)

检测的函数

传入的适应度函数为

def aimfunc1(x1,y1):
    """"f1的目标函数"""
    func1_result =1/(x1**2+y1**2)
    print('x1 = ',x1)
    print('y1 = ',y1)
    print('解是 ......',1/func1_result)
    return func1_result

主函数

1.初始化种群
2.判断是否满足迭代次数，如果满足则停止迭代并图片显示最优解曲线，如果不满足，转入3
3.解码，代入适应度函数，根据累计概率进行轮盘赌选择，对编码列表进行交叉、变异，存储下来目标函数值最优值。进入2

import numpy as np
import math
import Two_DemiQST as TDQST
import  matplotlib.pyplot  as plt


t=[]
Init_bin(10,10,animal_population)     #初始化种群，种群数目，个体长度
for k in animal_population:
    print(k)
for i in range(1,200):				  #迭代次数200次
    Decode_Population_bin(10, animal_population, cur_population, 10, 5, 0.01, 5.12, 0.01, 5.12)   #解码种群
    aaa = Result_Population_bin_1(cur_population, TDQST.aimfunc1, result_population)              #得到目标函数值
    Rata_Population(result_population, rata_population)                                           #得到累计概率列表
    RoulettWheel(rata_population,select_population, animal_population)    						  #轮盘赌选择
    Crossover(select_population, 0.7)															  #交叉
    Mutation(select_population, 0.03)															  #变异
    #每次迭代只保留种群的编码列表，目标函数值列表，解码列表，累加概率列表。其中编码列表只保留最后选择的编码列表
    animal_population.clear() 																	  #清空初始化的编码列表
    for tmp in select_population:          														  #将最后选择的编码列表个体复制给初始化的编码列表
        animal_population.append(tmp)
    select_population.clear()  																	  #清空最后选择的编码列表
    cur_population.clear()																		  #清空解码列表
    rata_population.clear()																		  #清空累计概率列表
    aaa = 1/aaa;																				  #获得的目标函数值变为倒数并添加到打印列表
    t.append(aaa)																				 
    result_population.clear()																	  #清空目标函数值列表
    print('第'+str(i)+'代:'+str(aaa))                                                              #打印值
plt.figure("f1")                                                                                  #利用matplotlib库以图片展示
plt.plot(t)
plt.show()

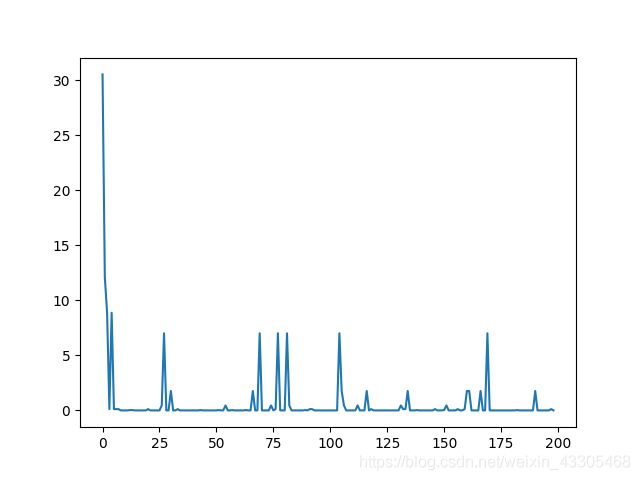
结果展示

纵坐标为目标函数的最优值，横坐标为迭代次数

print的结果为

结果分析

此处运用到的是最简单的遗传算法，二维问题，单点交叉，单点变异，二进制编码，只有一个目标函数。面对不同的优化问题，遗传算法有很大的改进，比如组合优化问题TSP问题中PMX交叉（部分映射交叉）、倒置变异；比如多目标优化问题中SBX(模拟二进制交叉)、多项式变异；另外进化思想的算法还有单目标问题的EP、ES、GP多目标优化问题的NSGA-II、MOE/A等算法。本文仅仅是一个最简单的例子。对于此次解决此类问题，适应度函数直接决定了收敛速度，取倒数的时候在进行轮盘赌选择的时候更容易选择出最优解，使得函数能够快速收敛，但是这也存在一个问题，对于变异的个体十分敏感。
个人感觉遗传算法中的需要注意的核心在于适应度函数的选择。虽说随机选择选择出最优解的情况存在，但是对于解决不同的函数，适应度函数的选择要考虑，目标函数是否全为正数，是求最大值还是最小值等问题。适应度函数的好坏决定了你的收敛速度！

水平有限，如有错误，欢迎指出！