ROS全覆盖规划算法逻辑整理笔记
一,规划算法包描述
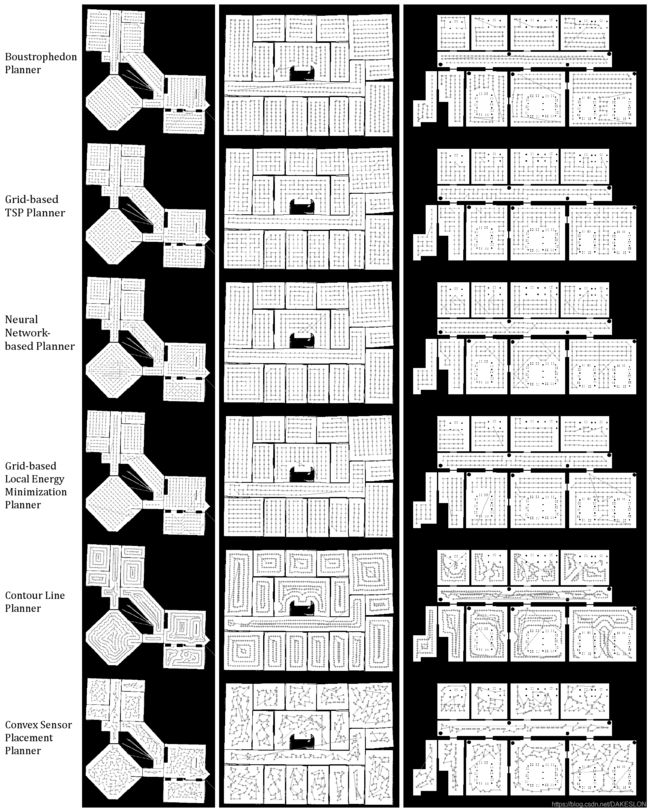
ROS提供了计算全覆盖路径的功能包,里面有几种计算全覆盖路径的方式,每种计算方式都有其特点以及不同的使用场景,具体可以查看官网 ipa_room_exploration - ROS Wiki,下面引用官方的一张图来简单说明一下每一种覆盖算法的特点:
在实际的应用场景中,比如智能清洁机器人领域,使用第一种分区覆盖算法即牛耕法比较贴合应用场景,故下面就专门针对该算法的具体实现做一个流程分析。
二,整体逻辑分析
这部分开源代码的源码在https://github.com/ipa-rmb/autopnp 上可以找到,源码下载好后分区覆盖的代码处于ipa_room_exploration文件夹内,调用算法的接口代码在room_exploration_action_server.h里面。
调用接口定义如下:
void exploreRoom(const ipa_building_msgs::RoomExplorationGoalConstPtr &goal);整体的处理逻辑流程图如下:
在exploreRoom()函数里面,预处理部分,会先根据传入的机器人的半径算出覆盖线的间距,接下来对传入的地图数据进行图像预处理(源码里面只是进行简单的腐蚀膨胀),调用removeUnconnectedRoomParts(room_map);移除掉不连通区域,最终保留下面积最大的一个连通区域,接下来就是调用具体的实现算法,源码里面包含多种算法实现接口,牛耕法则是调用boustrophedon_explorer_.getExplorationPath()获得全覆盖路径,下面对该函数做一个详细分析。
函数接口定义如下:
// Function that creates an exploration path for a given room. The room has to be drawn in a cv::Mat (filled with Bit-uchar),
// with free space drawn white (255) and obstacles as black (0). It returns a series of 2D poses that show to which positions
// the robot should drive at.
void getExplorationPath(const cv::Mat& room_map, std::vector& path, const float map_resolution,
const cv::Point starting_position, const cv::Point2d map_origin, const double grid_spacing_in_pixel,
const double grid_obstacle_offset, const double path_eps, const int cell_visiting_order, const bool plan_for_footprint,
const Eigen::Matrix robot_to_fov_vector, const double min_cell_area, const int max_deviation_from_track);
进入该函数,首先会先调用 computeCellDecompositionWithRotation(),该函数实现两个功能,第一个是对地图进行长短边计算,计算得出最佳的旋转矩阵,并将地图进行旋转。第二则是调用computeCellDecomposition()函数进行区间分割,具体的分区实现逻辑后续再讲,该函数返回每一个区间的多边形点数组cell_polygons以及每一个区间的中心点数组polygon_centers。返回的cell_polygons用来确定区间在地图上的位置,polygon_centers则是用来确定区间跟区间之间的距离。
区间分割完成后,则接下来根据polygon_centers计算多个区间的遍历顺序,源码中提供了两种计算区间遍历顺序的方式:
if (cell_visiting_order == OPTIMAL_TSP)
{...}
else if (cell_visiting_order == LEFT_TO_RIGHT)
{...}第一种是通过TSP计算得出区间遍历顺序,第二种则是简单的通过polygon_centers的Y坐标从小到大排序。第二种计算方式比较简单就不再阐述,关键需要看看第一种的实现方式,官方给出的源码是这样子的:
if (cell_visiting_order == OPTIMAL_TSP)
{
// determine the optimal visiting order of the cells
// ConcordeTSPSolver tsp_solver;
// std::vector optimal_order = tsp_solver.solveConcordeTSP(rotated_room_map, polygon_centers, 0.25, 0.0, map_resolution, start_cell_index, 0);
GeneticTSPSolver tsp_solver;
optimal_order = tsp_solver.solveGeneticTSP(rotated_room_map, polygon_centers, 0.25, 0.0, map_resolution, start_cell_index, 0);
if (optimal_order.size()!=polygon_centers.size())
{
std::cout << "=====================> Genetic TSP failed with 25% resolution, falling back to 100%. <=======================" << std::endl;
optimal_order = tsp_solver.solveGeneticTSP(rotated_room_map, polygon_centers, 1.0, 0.0, map_resolution, start_cell_index, 0);
}
}
其中,官方默认使用的是GeneticTSPSolver ,即用遗传算法来求解区间遍历顺序,但是在实际的使用场景中并不是一种相对较好的方式,源码中还提供了另一种计算区间遍历顺序的方式,源码的文件位置为autopnp/ipa_building_navigation/common/src/nearest_neighbor_TSP.cpp,这是一种通过计算最临近区域求出TSP近似解的方式。源码的具体实现逻辑以及优化思路后续再补充。
上述操作完成后,就得到各个子区间以及区间的遍历顺序,接下来则是要计算各区间内的弓字形覆盖路线,源码实现该逻辑的代码如下:
for(size_t cell=0; cell其中, rotated_room_map为经过矩阵旋转后的地图, optimal_order为生成的区间遍历顺序,fov_middlepoint_path 为生成的总的覆盖直线点,robot_pos为机器人坐标(注意该坐标在每次计算后都会发生改变), grid_spacing_as_int为覆盖直线的宽度, path_eps控制生成路径点的疏密。具体的弓字形覆盖路径计算逻辑同样后续再补充。
经过上述操作,就可以计算得出覆盖直线,但由于是在旋转后的地图上进行计算得出的,故还需要通过旋转矩阵将坐标点仿射变换到原图上:
room_rotation.transformPathBackToOriginalRotation(fov_middlepoint_path, fov_poses, R);完成上述步骤后,得到的坐标点是图像上的坐标点,故最后需要转换坐标系。源码中实现该功能的代码如下:
// *********************** V. Get the robot path out of the fov path. ***********************
// go trough all computed fov poses and compute the corresponding robot pose
cv::Point robot_starting_position = (fov_poses.size()>0 ? cv::Point(cvRound(fov_poses[0].x), cvRound(fov_poses[0].y)) : starting_position);
cv::Mat inflated_room_map;
cv::erode(room_map, inflated_room_map, cv::Mat(), cv::Point(-1, -1), half_grid_spacing_as_int);
mapPath(inflated_room_map, path, fov_poses, robot_to_fov_vector, map_resolution, map_origin, robot_starting_position);
其中, mapPath()的功能是进行坐标转换的同时,把一些贴近障碍物的坐标点给去掉。
至此,就生成了该地图的全覆盖遍历坐标点。