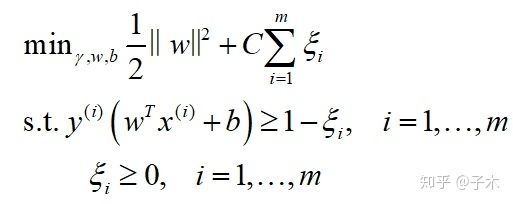基于MATLAB的LS-SVM实现方法以及SVM的一些知识点

使用之前需要把LSSVMlabv1_8_R2009b_R2011a解压 并在matlab中添加到路径中

下载链接：http://www.esat.kuleuven.be/sista/lssvmlab/

我使用的是 V1.8版本。

matlab版本我使用的是2019a。

关于SVM具体叙述可以看这篇文章：

 SVM(支持向量机)原理及数学推导全过程详解

这里不具体说LS-SVM原理了，主要介绍MATLAB实现LS-SVM的步骤。

In Support Vector Machines (SVMs), the solution of the classification problem is characterized by a (convex) quadratic programming (QP) problem. In a modified version of SVMs, called Least Squares SVM classifiers (LS-SVMs), a least-squares cost function is proposed so as to obtain a linear set of equations in the dual space.

目录

一、机器学习中常用的一些名词

1.偏差与方差

2. SVM的参数gamma(γ)，惩罚因子C，正则化参数Lambda(λ)

二、LS-SVM工具箱实例的一些参数

2.1 模型参数

2.2 输入样本以及函数参数

三、LS-SVM工具箱函数使用方法

四、LS-SVM完整实现过程

4.1 使用参数的方法

4.2 使用接口的方法

五、重点是关于寻优的方法

六、多分类LS-SVM

---

一、机器学习中常用的一些名词

1.偏差与方差

偏差（bias）：偏差是衡量期望预测值和真实值的偏离程度。即N次预测的平均值（也叫期望值），和实际真实值的差距。所以偏差bias=E(p(x)) - f(x)。
即bias是指一个模型在不同训练集上的平均表现和真实值的差异，用来衡量一个模型的拟合能力，刻画了学习算法本身的拟合能力。

方差（variance）：方差用于衡量预测值之间的关系，和真实值无关。即对于给定的一个预测模型，N次预测结果之间的方差，度量了同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所造成的影响。variance= E((p(x) - E(p(x)))^2)。这个公式就是数学里的方差公式，反应的是统计量的离散程度。

也可以这样描述：训练数据在不同迭代阶段的训练模型中，预测值的变化波动情况（或称之为离散情况）。从数学角度看，可以理解为每个预测值与预测均值差的平方和的再求平均数。通常在模型训练中，初始阶段模型复杂度不高，为低方差；随着训练量加大，模型逐步拟合训练数据，复杂度开始变高，此时方差会逐渐变高。
即variance指一个模型在不同训练集上的差异，用来衡量一个模型是否容易过拟合。

一般训练程度越强，偏差越小，方差越大，泛化误差一般在中间有一个最小值，如果偏差较大，方差较小，此时一般称为欠拟合，而偏差较小，方差较大称为过拟合。

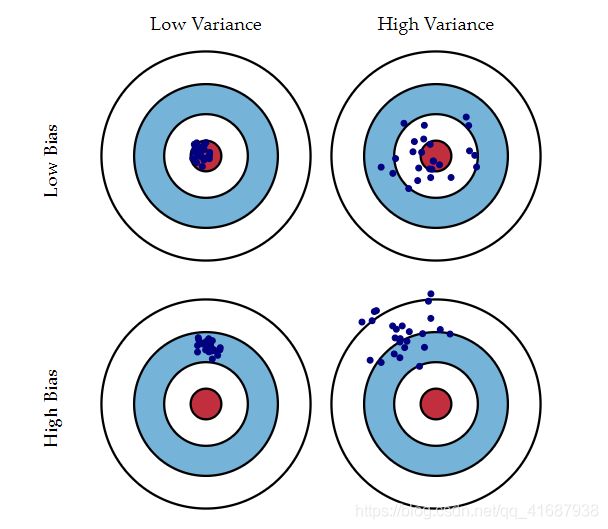
1.1 以下面的打靶图为例进行解释：

先搞清楚图中各元素的含义！红色中心代表目标值，每一个蓝点，都代表了一个训练模型的预测数据，即根据不同的训练集训练出一个训练模型，再用这个训练模型作出一次预测结果。

左下角的“打靶图”，假设我们的目标是中心的红点，所有的预测值都偏离了目标位置，这就是偏差；
在右上角的“打靶图”中，预测值围绕着红色中心周围，没有大的偏差，但是整体太分散了，不集中，这就是方差。

 

• 低偏差，低方差：这是训练的理想模型，此时蓝色点集基本落在靶心范围内，且数据离散程度小，基本在靶心范围内；
• 低偏差，高方差：这是深度学习面临的最大问题，过拟合了。也就是模型太贴合训练数据了，导致其泛化（或通用）能力差，若遇到测试集，则准确度下降的厉害。通过对偏差的定义，不难发现，偏差是一个期望值（平均值），如果一次射击偏左5环，另一次射击偏右5环，最终偏差是0。但是没一枪打中靶心，所以方差是巨大的，这种情况也是需要改进的。
• 高偏差，低方差：这往往是训练的初始阶段。每次射击都很准确的击中同一个位置，故极端的情况方差为0。只不过，这个位置距离靶心相差了十万八千里。对于射击而言，每次都打到同一个点，很可能是因为它打的不是靶心。对于模型而言，往往是因为模型过于简单，才会造成“准”的假象。提高模型的复杂度，往往可以减少高偏差。
• 高偏差，高方差：这是训练最糟糕的情况，准确度差，数据的离散程度也差。

1.2 以stanford课程《机器学习》的说法

偏差和方差

通常用代价函数J（平方差函数）评价数据拟合程度好坏。如果只关注Jtrain(训练集误差)的话，通常会导致过拟合，因此还需要关注Jcv(交叉验证集误差)。

高偏差：Jtrain和Jcv都很大，并且Jtrain≈Jcv。对应欠拟合。

高方差：Jtrain较小，Jcv远大于Jtrain。对应过拟合。

下图d代表多项式拟合的阶数，d越高，拟合函数越复杂，越可能发生过拟合。

1、高偏差对应着欠拟合，此时Jtrain也较大，可以理解为对任何新数据（不论其是否属于训练集），都有着较大的Jcv误差，偏离真实预测较大。
2、高方差对应着过拟合，此时Jtrain很小，对于新数据来说，如果其属性与训练集类似，它的Jcv就会小些，如果属性与训练集不同，Jcv就会很大，因此有一个比较大的波动，因此说是高方差。

模型修改策略

高方差，过拟合：增大数据规模、减小数据特征数（维数）、增大正则化系数λ

高偏差，欠拟合：增多数据特征数、添加高次多项式特征、减小正则化系数λ

实际优化过程中，我们的目标就是使模型处于欠拟合和过拟合之间一个平衡的位置。   

1.3 模型误差
模型误差 = 偏差 + 方差 + 不可避免的误差（噪音）。一般来说，随着模型复杂度的增加，方差会逐渐增大，偏差会逐渐减小，见下图：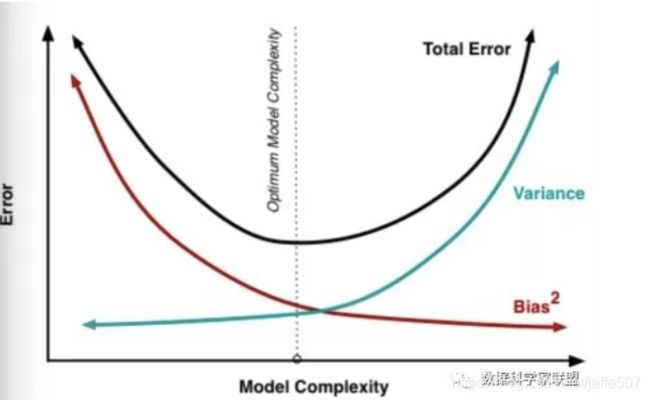

 

2. SVM的参数gamma(γ)，惩罚因子C，正则化参数Lambda(λ)

2.1 惩罚因子C

在SVM的理论分析中我们知道决策平面与支持向量之间有一个距离差，而在实际工程中，参数c正是影响了支持向量与决策平面之间的距离。先看看公式：

C是惩罚因子，决定了你有多重视离群点带来的损失，有的资料解释为对误差的容忍度，其实这句话提到的误差不是误差。具体效果为：

c越大，分类越严格，不能有错误，容易过拟合；

c越小，意味着有更大的错误容忍度，容易欠拟合。

具体可以通过下图展示：

c越大分类结果越好相应的泛化能力降低，c越小，我们的决策边界更大一些，即在训练时容忍一些样本的误差，拿一些边界更宽的样本作为支持向量。

2.2 正则化参数Lambda(λ)

使用处理机器学习中的目标函数时，有时会发生过拟合。此时常常对模型的参数做一定的限制，使得模型偏好更简单的参数，这就叫“正则化”（regularization）。
最常见的正则化方法，就是（软性地）限制参数的大小。
设目标函数是要最小化的，所有参数组成向量w。
如果往目标函数上加上（参数向量w的L1范数），这就是L1正则化；
如果往目标函数上加上（参数向量w的L2范数的平方的一半），这就是L2正则化。
L1正则化的优点是优化后的参数向量往往比较稀疏；L2正则化的优点是其正则化项处处可导。

SVM并不是“损失函数”、“正则化”等概念的典型例子。

但是在SVM中正则化参数与惩罚因子成倒数关系，C=1/λ。

所以在SVM的算法中没再提到正则化参数。

2.3 gamma(γ)参数

gamma是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了对低维的样本进行高维映射到新的特征空间后的分布。

根据RBF公式里面的sigma和gamma的关系如下：

 这里面大家需要注意的就是gamma的物理意义，大家提到很多的RBF的幅宽，它会影响每个支持向量对应的高斯的作用范围，从而影响泛化性能。我的理解：如果gamma设的太大，sgm(σ)会很小，sgm(σ)很小的高斯分布长得又高又瘦， 会造成只会作用于支持向量样本附近，对于未知样本分类效果很差，存在训练准确率可以很高，(如果让sgm(σ)无穷小，则理论上，高斯核的SVM可以拟合任何非线性数据，但容易过拟合)而测试准确率不高的可能，就是通常说的过拟合；而如果设的过小，则会造成平滑效应太大，无法在训练集上得到特别高的准确率，也会影响测试集的准确率。

总结来说就是：

gamma越大，映射的维度越高，训练的结果越好，支持向量越少，但是越容易引起过拟合，即泛化能力低。

gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度，而且也会影响准确率。

 

总结：

过拟合：减小C或gamma；

欠拟合：增大C或gamma。

 

 

二、LS-SVM工具箱实例的一些参数

2.1 模型参数

根据原文：

In order to make an LS-SVM model (with Gaussian RBF kernel), we need two tuning parame-
ters: γ (gam) is the regularization parameter, determining the trade-off between the training error
minimization and smoothness. In the common case of the Gaussian RBF kernel, σ2(sig2) is the
squared bandwidth.

所以实用工具时候的一些参数是存在出入的，需要进行对应。

即：

工具箱中的γ (gam)指的不是上面提到的高斯核参数gamma(γ)，而是与惩罚因子C是倒数关系的；

工具箱中的σ2(sig2)与高斯核参数gamma(γ)关系如下：

2.2 输入样本以及函数参数

这个直接在函数使用的地方说。

三、LS-SVM工具箱函数使用方法

3.1 函数参数

在一个完整的训练流程中，每个函数一定要使用相同的参数选项！比如数据是否初始化，在每个函数中都要保持一致。

参数含义：X代表训练样本(每一行为一个样本，则每一列为一维特征)；

                  Y代表训练样本标签；

                  type有两种类型,classfication, 用于分类, function estimation, 用于函数回归；

                 'RBF_kernel'代表使用的是径向基核函数，还包括lin_kernel、poly_kernel、MLP_kernel

                  preprocess是数据已经进行归一化,′original ′是数据没有进行归一化, 缺省时是′preprocess′

                 'simplex' 通过在参数空间穷尽对比得到最好的参数。是simplex单纯形法(模拟退火法，工具箱默认方法).%'gridsearch'是二次规划法 

                 crossvalidatelssvm代表使用交叉验证进行寻优

                 L-fold代表采用L折交叉验证

3.2 涉及到的函数

寻参函数：tunelssvm

作用：根据寻优方法找到当前输入训练集所对应的的最优gam,sig2。其实在函数内部进行了模型训练，最后取的准确率最高的一组参数。

使用示例： 

[gam,sig2] = tunelssvm({X,Y,type,[],[],'RBF_kernel','preprocess'},'simplex',...
'crossvalidatelssvm',{L_fold,'misclass'});

接口函数：initlssvm

作用：将训练模型当做句柄使用。示例：

model = initlssvm(X,Y,type,[],[],’RBF_kernel’);

model = tunelssvm(model,’simplex’,’crossvalidatelssvm’,{L_fold,’misclass’});

还包括训练函数，预测函数，画图函数，ROC曲线函数。

具体看例子吧，很简单的使用，注释很详细，没必要重复说。

四、LS-SVM完整实现过程

4.1 使用参数的方法

close all;clear;clc;
X = 2.*rand(100,2)-1;
Y = sign(sin(X(:,1))+X(:,2));
%% 参数设置
% gam = 10;sig2 = 0.2;%可以指定，也可以参数寻优找到

type = 'classification';
L_fold = 10; % L-fold crossvalidation
[gam,sig2] = tunelssvm({X,Y,type,[],[],'RBF_kernel','preprocess'},'simplex',...
'crossvalidatelssvm',{L_fold,'misclass'});%寻优方法还可选'gridsearch'

%% 模型训练和图形化显示 
[alpha,b] = trainlssvm({X,Y,type,gam,sig2,'RBF_kernel','preprocess'});
plotlssvm({X,Y,type,gam,sig2,'RBF_kernel','preprocess'},{alpha,b});

%% 利用训练模型进行预测
Xt = 2.*rand(10,2)-1;
disp(' >> Ytest = simlssvm({X,Y,type,gam,sig2,''RBF_kernel'',''preprocess''},{alpha,b},Xt);');
Ytest = simlssvm({X,Y,type,gam,sig2,'RBF_kernel','preprocess'},{alpha,b},Xt);

%% 利用公式计算真实值，并与模型预测结果进行对比
YY = sign(sin(Xt(:,1))+Xt(:,2));
figure
subplot(2,1,1)
plot(Xt,Ytest,'*'); title('模型预测结果','fontsize',13); 
subplot(2,1,2)
plot(Xt,YY,'*'); title('公式计算结果','fontsize',13); 

ypred = length(find(Ytest==YY))/(length(Ytest)) * 100;
disp(['accuracy = ' ,num2str(ypred),'%'])

%% ROC曲线
Y_latent = latentlssvm({X,Y,type,gam,sig2,'RBF_kernel'},{alpha,b},X); %需要潜在的变量来制作ROC曲线
[area,se,thresholds,oneMinusSpec,Sens]=roc(Y_latent,Y);
[thresholds oneMinusSpec Sens];

4.2 使用接口的方法

%% load 数据
close all;clear;clc;
X = 2.*rand(100,2)-1;
Y = sign(sin(X(:,1))+X(:,2));

type = 'classification';
L_fold = 10; % L-fold crossvalidation

%% 获得对象接口
model = initlssvm(X,Y,type,[],[],'RBF_kernel');

%% 参数寻优
model = tunelssvm(model,'simplex','crossvalidatelssvm',{L_fold,'misclass'});

%% 模型训练和图形化显示 
model = trainlssvm(model);
plotlssvm(model);

%% 利用训练模型进行预测
Xt = 2.*rand(10,2)-1;
Ytest = simlssvm(model,Xt);

%% 利用公式计算真实值，并与模型预测结果进行对比
YY = sign(sin(Xt(:,1))+Xt(:,2));
figure
subplot(2,1,1)
plot(Xt,Ytest,'*'); title('模型预测结果','fontsize',13); 
subplot(2,1,2)
plot(Xt,YY,'*'); title('公式计算结果','fontsize',13); 

ypred = length(find(Ytest==YY))/(length(Ytest)) * 100;
disp(['accuracy = ' ,num2str(ypred),'%'])

%% ROC曲线
% latent variables are needed to make the ROC curve
Y_latent = latentlssvm(model,X);
[area,se,thresholds,oneMinusSpec,Sens]=roc(Y_latent,Y);
[thresholds oneMinusSpec Sens];

五、重点是关于寻优的方法

本文上面使用的是默认的模拟退火法，还可以使用遗传算法，粒子群算法实现。

六、多分类LS-SVM

这里介绍的是二分类SVM，下一篇介绍一下多分类LS-SVM，利用工具箱并不麻烦。将输入标签在训练模型前进行编码，预测后进行解码就可以。