动手学深度学习Pytorch(一)——多层感知机
文章目录
- 1. 参考资料
- 2. 感知机
- 3. 多层感知机
-
- 3.1 隐藏层
- 3.2 激活函数
-
- 3.2.1 Sigmoid激活函数
- 3.2.2 Tanh激活函数
- 3.2.3 ReLu激活函数
- 3.3 多类分类
1. 参考资料
[1] 动手学深度学习 v2 - 从零开始介绍深度学习算法和代码实现
课程主页:https://courses.d2l.ai/zh-v2/
教材:https://zh-v2.d2l.ai/
[2] 李沐老师B站视频:https://www.bilibili.com/video/BV1MB4y1F7of?p=3
2. 感知机
(1)定义
给定输入x,权重w,和偏移b,感知机输出:
o = σ ( < w , x > + b ) o=\sigma(
(2)训练感知机
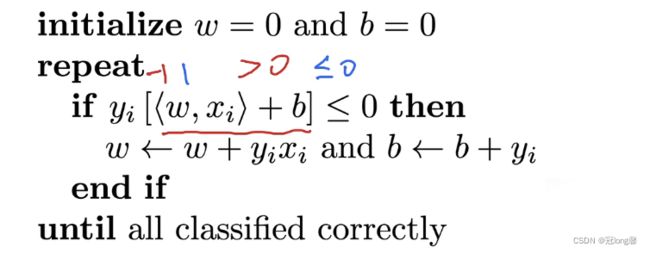
等价于批量大小为1的梯度下降,损失函数为:
l ( y , x , w ) = max ( 0 , y < w , x > ) l(y,x,w) = \max(0,y
其中,偏置值b加入到x和w中。当分类正确时 y < w , x > > 0 y
(3)收敛定理
- 数据在半径r内
- 余量 ρ ( ρ > 0 ) \rho(\rho>0) ρ(ρ>0)分类两类
y ( x T w + b ) ≥ ρ y(x^Tw+b) \geq \rho y(xTw+b)≥ρ - 感知机保证在 r 2 + 1 ρ 2 \frac{r^2+1}{\rho^2} ρ2r2+1步后收敛
(4)总结
- 感知机只能拟合线性分类问题,而不能处理非线性问题。
- 求解算法等价于批量大小为1的梯度下降。
3. 多层感知机
超参数
- 隐藏层数
- 每层隐藏层的大小
- 学习率
3.1 隐藏层
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。
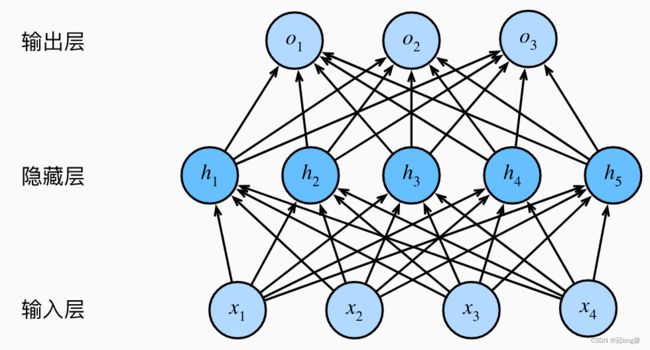
单分类
- 输入 x ∈ R n x \in R^n x∈Rn
- 隐藏层 W 1 ∈ R m × n , b 1 ∈ R m W_1 \in R^{m \times n},b_1 \in R^m W1∈Rm×n,b1∈Rm
- 输出层 W 2 ∈ R m , b 2 ∈ R W_2 \in R^{m},b_2 \in R W2∈Rm,b2∈R
h = σ ( W 1 x + b 1 ) o = W 2 T h + b 2 h = \sigma(W_1x+b_1) \\ o = W_2^T h+b_2 h=σ(W1x+b1)o=W2Th+b2
3.2 激活函数
激活函数将输入信号转换为输出的可微信号。大多数激活函数都是非线性的。
为什么需要非线性激活函数?
因为如果不加激活函数,输出仍然是线性结果,与线性函数功能相同。
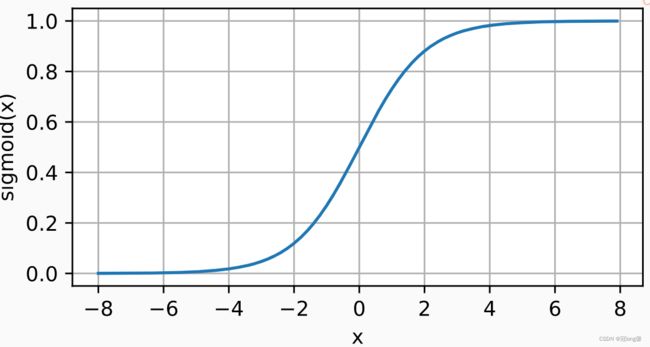
3.2.1 Sigmoid激活函数
将输入投影到 ( 0 , 1 ) (0,1) (0,1):
s i g m o i d ( x ) = 1 1 + exp ( − x ) sigmoid(x) = \frac{1}{1+\exp(-x)} sigmoid(x)=1+exp(−x)1
- 它是一个平滑的、可微的阈值单元近似。
- 在隐藏层中较少使用,在大部分时候被更简单、更容易训练的ReLU所取代。
3.2.2 Tanh激活函数
将输入投影到 ( − 1 , 1 ) (-1,1) (−1,1):
t a n h ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) tanh(x) = \frac{1-\exp(-2x)}{1+\exp(-2x)} tanh(x)=1+exp(−2x)1−exp(−2x)
- 相同点:输入在任意方向远离0点,导数越接近于0.
- 不同点1:当输入在0附近时,tanh函数接近线性变换
- 不同点2:tanh函数关于坐标系原点中心对称。
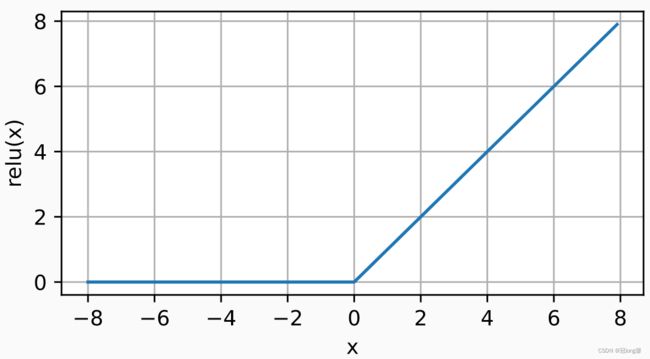
3.2.3 ReLu激活函数
ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素。
R e L u ( x ) = max ( x , 0 ) ReLu(x) = \max(x,0) ReLu(x)=max(x,0)
- 当输入为负时,ReLu的导数为0.当输入为正时,ReLu的导数为1.当输入为0时,默认使用导数为0.
- 优化表现更好:ReLu要么让参数消失,要么让参数通过。
- 减轻了梯度消失问题。
3.3 多类分类
多类分类
相比于softmax就是多了一层非线性隐藏层。
- 输入 x ∈ R n x \in R^n x∈Rn
- 隐藏层 W 1 ∈ R m × n , b 1 ∈ R m W_1 \in R^{m \times n},b_1 \in R^m W1∈Rm×n,b1∈Rm
- 输出层 W 2 ∈ R m × k , b 2 ∈ R k W_2 \in R^{m \times k},b_2 \in R^k W2∈Rm×k,b2∈Rk
h = σ ( W 1 x + b 1 ) o = W 2 T h + b 2 y = s o f t m a x ( o ) h = \sigma(W_1x+b_1) \\ o = W_2^T h+b_2 \\ y = softmax(o) h=σ(W1x+b1)o=W2Th+b2y=softmax(o)