李沐动手学深度学习第4章-4.2多层感知机的从零开始实现
现在让我们尝试自己实现一个多层感知机。 为了与之前softmax回归获得的结果进行比较, 我们将继续使用Fashion-MNIST图像分类数据集。
代码如下:
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)1. 初始化模型参数
Fashion-MNIST中的每个图像由 28×28=784个灰度像素值组成。 所有图像共分为10个类别。 忽略像素之间的空间结构, 我们可以将每个图像视为具有784个输入特征 和10个类的简单分类数据集。 首先,我们将实现一个具有单隐藏层的多层感知机, 它包含256个隐藏单元。
对于每一层我们都要记录一个权重矩阵和一个偏置向量。 跟以前一样,我们要为损失关于这些参数的梯度分配内存。
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]2. 激活函数
为了确保我们对模型的细节了如指掌, 我们将实现ReLU激活函数, 而不是直接调用内置的relu函数。
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)3. 模型
因为我们忽略了空间结构, 所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。 只需几行代码就可以实现我们的模型。
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法
return (H@W2 + b2)4. 损失函数
直接使用高级API中的内置函数来计算softmax和交叉熵损失。
loss = nn.CrossEntropyLoss(reduction='none')5. 训练
多层感知机的训练过程与softmax回归的训练过程完全相同。 可以直接调用d2l包的train_ch3函数, 将迭代周期数设置为10,并将学习率设置为0.1.
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)6、预测
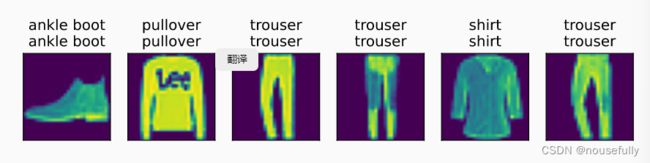
d2l.predict_ch3(net, test_iter)