联邦学习——FedAvg《Communication-Efficient Learning of Deep Networks from Decentralized Data》论文笔记

---

最近开始了解联邦学习相关的内容，阅读了比较经典的FedAvg算法,并记录了一点笔记，如有错误，欢迎指正，感谢！

论文链接

《Communication-Efficient Learning of Deep Networks from Decentralized Data》

---

一、摘要

Modern mobile devices have access to a wealth of data suitable for learning models, which in turn
can greatly improve the user experience on the device. For example, language models can improve speech recognition and text entry, and image models can automatically select good photos.However, this rich data is often privacy sensitive,large in quantity, or both, which may preclude logging to the data center and training there using conventional approaches. We advocate an alternative that leaves the training data distributed on the mobile devices, and learns a shared model by aggregating locally-computed updates. We term this decentralized approach Federated Learning.

现代移动设备可以访问大量适合学习模型的数据，这反过来又可以极大地改善设备上的用户体验。例如，语言模型可以提高语音识别和文本输入，图像模型可以自动选择好的照片。然而，这些丰富的数据通常对隐私敏感、数量庞大，或者两者兼有，这可能会妨碍登录数据中心并使用传统方法在那里进行培训。我们提倡一种替代方法，将训练数据分布在移动设备上，并通过聚合本地计算的更新来学习共享模型。我们称这种分散的方法为联邦学习。

We present a practical method for the federated learning of deep networks based on iterative
model averaging, and conduct an extensive empirical evaluation, considering five different model ar-chitectures and four datasets. These experiments demonstrate the approach is robust to the unbal-
anced and non-IID data distributions that are a defining characteristic of this setting. Communication costs are the principal constraint, and we show a reduction in required communication rounds by 10–100× as compared to synchronized stochastic gradient descent.

文章考虑到五种不同的模型架构和四个数据集，提出了一种基于迭代模型平均的深度网络联邦学习的实用方法，并进行了广泛的经验评估。这些实验表明，该方法对于不平衡和non-IID数据分布是稳健的，这是该设置的一个定义特征。通信成本是主要的限制因素，与同步随机梯度(SGD)下降相比，我们显示所需的通信回合减少了10–100倍。

二、简介

We investigate a learning technique that allows users to collectively reap the benefits of shared models trained from this rich data, without the need to centrally store it. We term our approach Federated Learning, since the learning task is solved by a loose federation of participating devices (which we refer to as clients) which are coordinated by a central server. Each client has a local training dataset which is never uploaded to the server. Instead, each client computes an update to the current global model maintained by the server, and only this update is communicated. This is a direct application of the principle of focused collection or data minimization proposed by the 2012 White House report on privacy of consumer data [39]. Since these updates are specific to improving the current model, there is no reason to store them once they have been applied.

Google提出了一种模型学习范式，不需要集中移动端的数据到数据中心进行训练，从而保护了用户的隐私。服务器将全局模型（Global Model)下发给客户端（Client)，客户端利用本地数据集进行训练，并将训练后的权重上传到服务器，从而实现全局模型的更新。

We investigate a learning technique that allows users to collectively reap the benefits of shared models trained from this rich data, without the need to centrally store it. We term our approach Federated Learning, since the learning task is solved by a loose federation of participating devices (which we refer to as clients) which are coordinated by a central server. Each client has a local training dataset which is never uploaded to the server. Instead, each client computes an update to the current global model maintained by the server, and only this update is communicated. This is a direct application of the principle of focused collection or data minimization proposed by the 2012 White House report on privacy of consumer data [39]. Since these updates are specific to improving the current model, there is no reason to store them once they have been applied.

主要贡献是:
1)将来自移动设备的分散数据的训练问题确定为一个重要的研究方向；
2)选择可应用于该设置的简单实用的算法；
3)对所提出的方法的广泛的经验评估。更具体地说，我们引入了联邦平均算法，该算法将每个客户端上的局部随机梯度下降(SGD)与执行模型平均的服务器相结合。我们对该算法进行了大量实验，证明它对不平衡和非IID数据分布具有鲁棒性，并且可以将在分散数据上训练深度网络所需的通信次数减少几个数量级。

联邦学习Federated Learning：

Ideal problems for federated learning have the following properties:

1. Training on real-world data from mobile devices provides a distinct advantage over
   training on proxy data that is generally available in the data center.
2. This data is privacy sensitive or large in size (compared to the size of the model), so it is preferable not to log it to the data center purely for the purpose of model training (in service of the focused collection principle).
3. For supervised tasks, labels on the data can be inferred naturally from user interaction.

联合学习的问题具有以下特性:
1)在来自移动设备的真实世界数据上的训练比在数据中心通常可用的代理数据上的训练提供了明显的优势。
2)该数据对隐私敏感或规模较大(与模型的规模相比)，因此最好不要纯粹出于模型训练的目的将其记录到数据中心(服务于集中收集原则)。
3)对于监督任务，数据上的标签可以从用户交互中自然推断出来。

联邦优化Federated Optimization

将联邦学习中隐含的优化问题称为联邦优化，与分布式优化建立了联系(和对比)。联合优化有几个关键属性，使其区别于典型的分布式优化问题:
1）non-iid，非独立同分布；
2）不平衡，不同用户的数据量不同；
3）用户分布是大规模的， 参与优化的用户数＞平均每个用户的数据量（这个不太确定理解的对不对）；
4）通信资源是有限的，移动设备经常掉线、速度缓慢、费用昂贵。

在本篇文章中，主要针对non-iid和不平衡的问题进行研究优化。

三、实验背景

We assume a synchronous update scheme that proceeds in rounds of communication. There is a fixed set of K clients, each with a fixed local dataset. At the beginning of each round, a random fraction C of clients is selected, and the server sends the current global algorithm state to each of these clients (e.g., the current model parameters). We only select a fraction of clients for efficiency, as our experiments show diminishing returns for adding more clients beyond a certain point. Each selected client then performs local computation based on the global state and its local dataset, and sends an
update to the server. The server then applies these updates to its global state, and the process repeats.

我们假设一个同步更新方案在几轮通信中进行。有一组固定的K个客户端，每个客户端都有一个固定的本地数据集。在每轮开始时，随机选择一部分客户端，服务器将当前全局算法状态发送给这些客户端中的每一个(例如，当前模型参数)。我们只选择一小部分客户来提高效率，因为我们的实验表明，增加超过某个点的客户会导致收益递减。然后，每个选定的客户端根据全局状态及其本地数据集执行本地计算，并向服务器发送更新。然后，服务器将这些更新应用到其全局状态，并重复该过程。

非凸神经网络的目标函数：
$$\underset{w\in {\mathbb{R}}^d}{\min }f(w)\text{ where }f(w)\stackrel{\text{ def }}{=}\frac{1}{n}\sum _{i=1}^n{f}_i(w).$$
对一个机器学习的问题来说，有$f_i(w)=\ell \left(x_i,y_i;w\right)$，即用模型参数$w$去预测实例（$x_i,y_i$）的损失。
假设现在有$K$个client，第$k$个client的数据点为${\mathcal{P}}_k$，对应的数据集数量为$n_k=|{\mathcal{P}}_k|$。则上式可写为：
$$f(w)=\sum _{k=1}^K\frac{n_k}{n}{F}_k(w)\text{ where }{F}_k(w)=\frac{1}{n_k}\sum _{i\in {\mathcal{P}}_k}{f}_i(w)$$
如果${\mathcal{P}}_k$上的数据集是随机均匀采样的，我们称为IID设置，此时有：
$${\mathbb{E}}_{{\mathcal{P}}_k}\left[F_k(w)\right]=f(w)$$
不成立则称为Non-iid设置。
举个例子，加入客户端为MNIST数据集，如果每个客户端的数据集都包含10个类别的样例，则为iid设置，否则则为non-iid设置（每个客户端有多少类别的样例，则可用non-iid程度来度量）。

四、联邦优化与传统集中优化的区别

在传统集中优化中，数据被集中到数据中心进行训练，计算成本占主导地位，通信成本几乎可以忽略不计。
而在联邦优化中，受到客户端和通信条件的影响，通信成本占据了主导地位，而计算成本反而可以忽略不计。

目标：通过使用额外的计算来减少训练模型所需的通信轮次

两种方法：
1)增加并行性，即在每轮通信之间使用更多独立工作的客户端；
2)每个客户端上的计算增加，其中每个客户端在每个通信回合之间执行更复杂的计算，而不是像梯度计算那样执行简单的计算。
我们研究了这两种方法，但是一旦使用了客户端上的最低并行级别，我们实现的加速主要是由于在每个客户端上增加了更多的计算。

五、FedAvg（FederatedAveraging） Algorithm

在深度学习中，最常用的用于优化的方法就是SGD（随机梯度下降），基于梯度来找到最优。
因此，SGD也可以简单的用于联邦优化。

• baseline——FedSGD

在每一轮中随机选择一组客户端，并计算损失梯度，注意只计算一次。
存在问题：需要大量的通信轮次才能取得较好的结果（因为每一轮通信内client只计算了一次）

接下来引入几个参数：

C, the fraction of clients thatperform computation on each round;
E, then number of training passes each client makes over its local dataset on each round;
B, the local minibatch size used for the client updates.
C表示每轮中选择参与的用户比例，当C=1时，表示所有用户参与；
E表示在一轮中，client在本地进行计算的epoch的数量，在FedSGD中，E=1；
B表示在一轮中，client在本地进行计算时的batchsize，在FedSGD中，B=$\infty$.

FedSGD只是FedAvg的一个特例，即当参数E=1，B=$\infty$时，FedAvg等价于FedSGD。
FedAvg算法细节如下：

这里借用一个别人画的FedSGD和FedAvg的关系示意图：

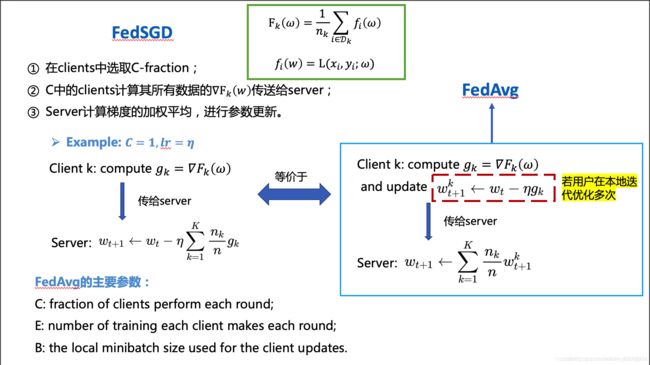
(地址：https://blog.csdn.net/biongbiongdou/article/details/104358321)

• 研究模型平均对模型效果的影响
  这里有两种情况，一种是不同模型使用不同的初始化模型；一种是不同模型使用相同的初始化模型
  并通过$\theta$参数对两个不同的模型的参数进行加权求和，绘制平均模型的loss曲线
  
  注意两条曲线的纵坐标不同，可看到，采用不同的初始化参数进行模型平均后，平均模型的效果变差，模型性能比两个父模型都差；采用相同的初始化参数进行模型平均后，对模型的平均可以显著的减少整个训练集的损失，模型性能优于两个父模型。
  这个点得到的结论是用于实现联邦学习的重要支撑，在每一轮训练时，server发布全局模型，使各个client采用相同的参数模型进行训练，可以有效的减少训练集的损失。

六、实验结果

1.增加并行性（每轮参与更新的用户数量）

• 模型设置（三个模型）

1. MNIST_2NN: 一个多层感知机，两个隐藏层，每个隐藏层有200个单元，使用ReLu激活函数，（199,210）个参数。
2. CNN:with two 5x5 convolution layers (the first with 32 channels, the second with 64, each followed with 2x2 max pooling), a fully connected layer with 512 units and ReLu activation, and a final softmax output layer (1,663,370 total parameters).

• IID和non-IID设置：

IID, where the data is shuffled, and then partitioned into 100 clients each receiving 600 examples, and Non-IID, where we first sort the data by digit label, divide it into 200 shards of size 300, and assign each of 100 clients 2 shards.

接下来对参数C,E,B进行讨论，固定参数E，对C和B进行讨论，对iid和non-iid的情况都进行实验：

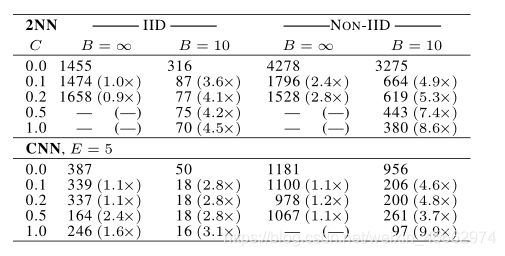
C表示每轮选取的客户数，上图记录了达到目标精度所需的轮次，可看出，对IID和non-iid而言，都有C越大，即选择的用户越多，所需的轮次减少，收敛的越快。而iid的趋势更加明显。且观察可看出，在选择的用户达到一定的数量时，收敛增加的速度不再明显，即选择的用户达到一定的数量后，再增加用户数量也无法明显增加收敛速度了。
在B=$\infty$下，增加用户数量取得的优势并不明显；在B=10的情况下，当C≥0.1时，收敛速度有明显的改进，因此后续的实验采用C=0.1。在计算效率与收敛速度取得平衡。

2.增加每个client的计算量

通过减少B或者增加E都可以使得client的计算量增加，每轮每个用户的更新次数可计算：
$$u=\left(\mathbb{E}\left[n_k\right]/B\right)E=nE/(KB)$$


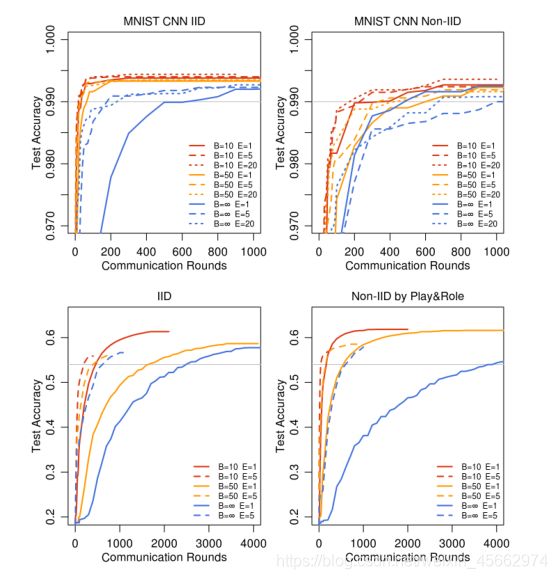
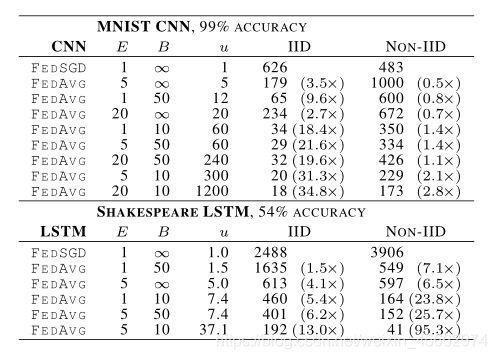
可见，对于IID情况，增速较快，对CNN能达到34.8倍，对于non-iid能达到2.8倍。但观察可知，对于莎士比亚数据集，使用LSTM模型，non-iid的表现反而比IID的好，推测可能是由于某些角色具有相对较大的本地数据集，这使得增加本地训练特别有价值。

3.其他模型数据集下的结果对比

FedSGD和FedAvg的学习率曲线对比：

SGD、FedSGD和FedAvg的轮次对比：

FedSGD和FedAvg的学习率曲线对比：