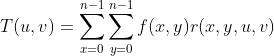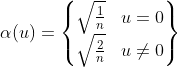KLT到DCT(杜克大学数字图像处理课程学习笔记)
在上网课时KL变换的讲授稍微有点绕,所以卡了好几天,个人感觉理解了,所以做一下记录,当然由于这个只是课程需要所以没有涉及整块的原理,如果需要还请看其他大神的数学原理解释
简单来讲,在不考虑中间量化的步骤时:
在图像压缩时经过压缩和解压缩重构出的图像与原图像的差距是通过MSE(均方误差)来衡量的
即:
![\sqrt{[\sum_{pixels}(f'-f)^2)/\left \| block \right \|]}](http://img.e-com-net.com/image/info8/6a59064adf6e47888ac73e111c662bc3.gif)
其中f ' 为重构生成的图像
f为原图
||block||代表分块压缩块的大小(这里假设块大小为n*n)
由这个原图经过变换之后我们会得到一个在KLT变换域中的新的n*n块
课中给出了这样的解释,如果我们将n*n块中除了第一个像素之外的其他系数全部删掉,再在解压缩阶段进行反变换得到重构图像,用上式计算均方误差时,我们将得到可能的最小误差,即,得到了变换后只用一个系数表示的最好结果
也就是说,如果我们将一个n*n块压缩为一个数,那么经过KL变换后得到的n*n个系数中的第一个系数就是我们进行这种规模的压缩下能得到的最好结果,换句话说,用这个数表示这个图像块能够丢失最少的数据
当然同样的,如果压缩到三个数字,就选前三个,m个数字就选前m个,在各种压缩规模下KL变换总能得到损失最小,最优的结果
这样我们就理解为什么KL变换是图像压缩的最理想算法
而DCT的可行性也与KLT有关,在满足马尔可夫条件的情况下,两者完全相同,即分块为8*8时
且DCT所做的周期性假设也是相对合理的,相邻的像素的值相似,对于图像来说很合理
这里简单叙述一下变换的本质
这部分其实是信号与系统的内容(我还没开始系统学变换的内容所以这里说的浅点):
在DCT的公式中:
![r(x,y,u,v)=\alpha (u)\alpha (v)cos[\frac{(2x+1)u\pi }{2n}]cos[\frac{(2y+1)u\pi }{2n}]](http://img.e-com-net.com/image/info8/4bf7b8a7caab46c7bfc67a17f0856a14.gif){kind=small}
其中,x,y的取值范围为0到n-1
由于r,
都是确定的,所以我们可以将T(u,v)看作是由f(x,y)决定的(虽然看起来像是废话,但是这个思维很重要),就是说这个变换的基底是确定的,然后你的结果是由输入决定的,其实也就是系统的概念
把u和v的值代入成具体的数字我们会发现,(以n=4为例),如图中有16个方块图,它们就是变换的基底,这些基底我们可以通过直接展开得到(不代入具体的f(x,y)),而我们的f(x,y)决定的T(u,v)的值对应的是第u行第v列的基底块的系数
例如如果我们的图是单色调图,那么我们只会有T(0,0)的系数,其他块系数都为0
我们的变换就是将一个图表示成一组基的线性组合
如此,再根据前述DCT与KLT在特定条件下等同,所以具有相同的性质,我们可以对变换域中的图做:取系数中的12.5% 这样类似的操作. 再对系数作逆DCT,我们将得到特定压缩规模下最优的压缩方案.