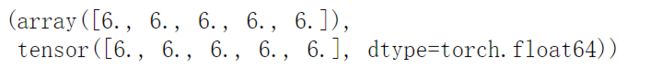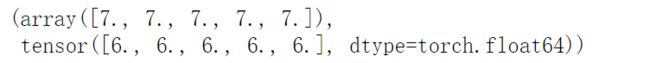Pytorch自定义神经网络构建
Pytorch基础与简单神经网络构建
- 01-Pytorch基础
-
- Tensor
- Cuda Tensor(Cpu/Gpu转换)
- Tensor运算
- index操作
- 内存问题
- 02-自定义model实现神经网络
01-Pytorch基础
Tensor
Tensor对象的3个属性:
- rank:number of dimensions
- shape: number of rows and columns
- type: data type of tensor’s elements
#Tensor实际上就是一个多维数组(multidimensional array),其目的是能够创造更高维度的矩阵、向量。
#初始化一个tensor
import torch
x = torch.empty(5,3)
x
#随机初始化矩阵
x = torch.rand(5,3)
x
#初始化为0
x = torch.zeros(5,3,dtype=torch.long)
x
#查看数据类型
x.dtype
#根据数据直接构建tensor
x1 = torch.tensor([6,8])
#根据已有tensor构建一个新tensor
x2 = x.new_ones(5,3).double()
x1,x2
#随机数据 同样纬度
x = torch.rand_like(x)
x,x.shape,x.size()
Cuda Tensor(Cpu/Gpu转换)
torch.cuda.is_available()
#将数据搬到GPU
device = torch.device("cuda")
x = torch.ones(3,3)
#01
y1 = torch.ones_like(x,device=device)
#02
y2 = x.to(device)
x,y1,y2
#从GPU拿到CPU
y1.to("cpu").data.numpy()
y2.cpu().data.numpy()
Tensor运算
y = torch.rand(5,3)
x = torch.rand(5,3)
#加法
result = torch.empty(5,3)
torch.add(x,y,out=result)#等价于result = x+y
#inplace 加法,直接复制给y
y.add_(x)
result,y
index操作
x = torch.rand(5,3)
x,x[1:,1:]
#reshape/resize操作
x = torch.randn(4,4)
y = x.view(16)
z = x.view(2,8)
a = x.view(-1,4)
b = x.view(4,-1)
x,y,z,a,b
#转为数字
x = torch.randn(1)
x,x.item()
内存问题
numpy 与 tensor互相转换的内存问题
#tensor->numpy
x = torch.ones(5)
y = x.numpy()
x,y
![]()
y[1]=2
x,y
![]()
#numpy -> tensor
import numpy as np
x = np.ones(5)
y = torch.from_numpy(x)
x,y
#共享内存1
np.add(x,2,out=x)
x,y
#共享内存2
x+=1
x,y
#不共享内存
x=x+1
x,y
02-自定义model实现神经网络
%%time
import torch
import torch.nn as nn
from tqdm.notebook import tqdm
#数据准备
N, D_in, H, D_out = 64,1000,100,1 # 输入数量,输入维数(特征数量),隐藏层神经元数,输出层数
x = torch.randn(N,D_in) # 输入数据x为N行,D_in列(特征数量)
y = torch.randn(N,D_out) # 输出数据y为N行,D_out列
#模型构建
class TwoLayerNet(torch.nn.Module):
def __init__(self,D_in,H,D_out):
super(TwoLayerNet,self).__init__()
self.linear1 = torch.nn.Linear(D_in,H,bias=False)
self.linear2 = torch.nn.Linear(H,D_out,bias=False)
def forward(self,x):
y_pred = self.linear2(self.linear1(x).clamp(min=0))
return y_pred
#定义模型传参
model = TwoLayerNet(D_in,H,D_out)
#定义损失函数
loss_fn = nn.MSELoss(reduction='sum')
#定义学习率以及epoche
learn_rate = 1e-4
epoches = 200
#定义优化器
#optimizer = torch.optim.Adam(model.parameters(),lr=learn_rate)
optimizer = torch.optim.SGD(model.parameters(),lr=learn_rate)
for it in tqdm(range(epoches)):
#执行前向传播
y_pred = model(x)
#执行计算损失函数
loss = loss_fn(y_pred,y)
#执行反向传播
loss.backward()
#执行优化器
optimizer.step()
#执行梯度归零
optimizer.zero_grad()
#输出误差
print("[%d/%d] Loss: %.5f" %(it+1, epoches, loss.item()))
[1/200] Loss: 56.81318
[2/200] Loss: 52.28790
[3/200] Loss: 48.18078
[4/200] Loss: 44.45538
[5/200] Loss: 41.07833
[6/200] Loss: 38.00413
[7/200] Loss: 35.18973
[8/200] Loss: 32.58974
[9/200] Loss: 30.17593
[10/200] Loss: 27.94987
[11/200] Loss: 25.88602
[12/200] Loss: 23.95603
[13/200] Loss: 22.14801
[14/200] Loss: 20.46547
[15/200] Loss: 18.89132
[16/200] Loss: 17.42441
[17/200] Loss: 16.06231
[18/200] Loss: 14.79838
[19/200] Loss: 13.62641
[20/200] Loss: 12.54109
[21/200] Loss: 11.53336
[22/200] Loss: 10.59185
[23/200] Loss: 9.71784
[24/200] Loss: 8.90829
[25/200] Loss: 8.15929
[26/200] Loss: 7.46851
[27/200] Loss: 6.82956
[28/200] Loss: 6.24042
[29/200] Loss: 5.69849
[30/200] Loss: 5.20201
[31/200] Loss: 4.74778
[32/200] Loss: 4.33064
[33/200] Loss: 3.94787
[34/200] Loss: 3.59618
[35/200] Loss: 3.27425
[36/200] Loss: 2.98037
[37/200] Loss: 2.71133
[38/200] Loss: 2.46567
[39/200] Loss: 2.24249
[40/200] Loss: 2.03894
[41/200] Loss: 1.85357
[42/200] Loss: 1.68443
[43/200] Loss: 1.53026
[44/200] Loss: 1.38997
[45/200] Loss: 1.26228
[46/200] Loss: 1.14630
[47/200] Loss: 1.04142
[48/200] Loss: 0.94589
[49/200] Loss: 0.85906
[50/200] Loss: 0.78027
[51/200] Loss: 0.70895
[52/200] Loss: 0.64400
[53/200] Loss: 0.58504
[54/200] Loss: 0.53148
[55/200] Loss: 0.48289
[56/200] Loss: 0.43877
[57/200] Loss: 0.39862
[58/200] Loss: 0.36221
[59/200] Loss: 0.32919
[60/200] Loss: 0.29920
[61/200] Loss: 0.27206
[62/200] Loss: 0.24742
[63/200] Loss: 0.22502
[64/200] Loss: 0.20464
[65/200] Loss: 0.18617
[66/200] Loss: 0.16942
[67/200] Loss: 0.15420
[68/200] Loss: 0.14040
[69/200] Loss: 0.12784
[70/200] Loss: 0.11644
[71/200] Loss: 0.10611
[72/200] Loss: 0.09673
[73/200] Loss: 0.08829
[74/200] Loss: 0.08063
[75/200] Loss: 0.07365
[76/200] Loss: 0.06729
[77/200] Loss: 0.06152
[78/200] Loss: 0.05625
[79/200] Loss: 0.05145
[80/200] Loss: 0.04708
[81/200] Loss: 0.04309
[82/200] Loss: 0.03946
[83/200] Loss: 0.03614
[84/200] Loss: 0.03311
[85/200] Loss: 0.03035
[86/200] Loss: 0.02783
[87/200] Loss: 0.02552
[88/200] Loss: 0.02342
[89/200] Loss: 0.02150
[90/200] Loss: 0.01974
[91/200] Loss: 0.01813
[92/200] Loss: 0.01666
[93/200] Loss: 0.01531
[94/200] Loss: 0.01408
[95/200] Loss: 0.01295
[96/200] Loss: 0.01191
[97/200] Loss: 0.01097
[98/200] Loss: 0.01010
[99/200] Loss: 0.00930
[100/200] Loss: 0.00857
[101/200] Loss: 0.00790
[102/200] Loss: 0.00728
[103/200] Loss: 0.00672
[104/200] Loss: 0.00620
[105/200] Loss: 0.00572
[106/200] Loss: 0.00528
[107/200] Loss: 0.00488
[108/200] Loss: 0.00451
[109/200] Loss: 0.00417
[110/200] Loss: 0.00385
[111/200] Loss: 0.00356
[112/200] Loss: 0.00330
[113/200] Loss: 0.00305
[114/200] Loss: 0.00282
[115/200] Loss: 0.00262
[116/200] Loss: 0.00242
[117/200] Loss: 0.00225
[118/200] Loss: 0.00208
[119/200] Loss: 0.00193
[120/200] Loss: 0.00179
[121/200] Loss: 0.00166
[122/200] Loss: 0.00154
[123/200] Loss: 0.00143
[124/200] Loss: 0.00133
[125/200] Loss: 0.00123
[126/200] Loss: 0.00115
[127/200] Loss: 0.00106
[128/200] Loss: 0.00099
[129/200] Loss: 0.00092
[130/200] Loss: 0.00086
[131/200] Loss: 0.00080
[132/200] Loss: 0.00074
[133/200] Loss: 0.00069
[134/200] Loss: 0.00064
[135/200] Loss: 0.00060
[136/200] Loss: 0.00056
[137/200] Loss: 0.00052
[138/200] Loss: 0.00048
[139/200] Loss: 0.00045
[140/200] Loss: 0.00042
[141/200] Loss: 0.00039
[142/200] Loss: 0.00037
[143/200] Loss: 0.00034
[144/200] Loss: 0.00032
[145/200] Loss: 0.00030
[146/200] Loss: 0.00028
[147/200] Loss: 0.00026
[148/200] Loss: 0.00024
[149/200] Loss: 0.00023
[150/200] Loss: 0.00021
[151/200] Loss: 0.00020
[152/200] Loss: 0.00018
[153/200] Loss: 0.00017
[154/200] Loss: 0.00016
[155/200] Loss: 0.00015
[156/200] Loss: 0.00014
[157/200] Loss: 0.00013
[158/200] Loss: 0.00012
[159/200] Loss: 0.00011
[160/200] Loss: 0.00011
[161/200] Loss: 0.00010
[162/200] Loss: 0.00009
[163/200] Loss: 0.00009
[164/200] Loss: 0.00008
[165/200] Loss: 0.00008
[166/200] Loss: 0.00007
[167/200] Loss: 0.00007
[168/200] Loss: 0.00006
[169/200] Loss: 0.00006
[170/200] Loss: 0.00006
[171/200] Loss: 0.00005
[172/200] Loss: 0.00005
[173/200] Loss: 0.00005
[174/200] Loss: 0.00004
[175/200] Loss: 0.00004
[176/200] Loss: 0.00004
[177/200] Loss: 0.00004
[178/200] Loss: 0.00003
[179/200] Loss: 0.00003
[180/200] Loss: 0.00003
[181/200] Loss: 0.00003
[182/200] Loss: 0.00003
[183/200] Loss: 0.00002
[184/200] Loss: 0.00002
[185/200] Loss: 0.00002
[186/200] Loss: 0.00002
[187/200] Loss: 0.00002
[188/200] Loss: 0.00002
[189/200] Loss: 0.00002
[190/200] Loss: 0.00002
[191/200] Loss: 0.00001
[192/200] Loss: 0.00001
[193/200] Loss: 0.00001
[194/200] Loss: 0.00001
[195/200] Loss: 0.00001
[196/200] Loss: 0.00001
[197/200] Loss: 0.00001
[198/200] Loss: 0.00001
[199/200] Loss: 0.00001
[200/200] Loss: 0.00001
Wall time: 216 ms