2021-11-04 学习周报
这其实是两周的学习周报,内容为三篇论文的学习总结:Transformer、ViT、Swin Transformer。
开山之作:Attention is all you need
Paper:《Attention Is All You Need》
Where:NIPS 2017
论文背景:
注意力机制可以利用人类视觉机制进行直观解释。例如,我们的视觉系统倾。同样,在涉及语言或视觉的问题中,输入的某些部分可能会比其他部分对决策更有帮助。例如,在翻译和总结任务中,输入序列中只有某些单词可能与预测下一个单词相关。同样,在image-caption问题中,输入图像中只有某些区域可能与生成caption的下一个单词更相关。注意力模型通过允许模型动态地关注有助于执行手头任务的输入的某些部分,将这种相关性概念结合起来。《Attention Is All You Need》提出,使用纯注意力机制就可以达到传统RNN和CNN的效果。
创新点:
Transformer网络架构基于attention mechanisms(注意力机制),完全舍弃了recurrence和convolutions,使用Self-attention层和FC层交替堆叠来组建Encoder和Decoder。
论文结构:
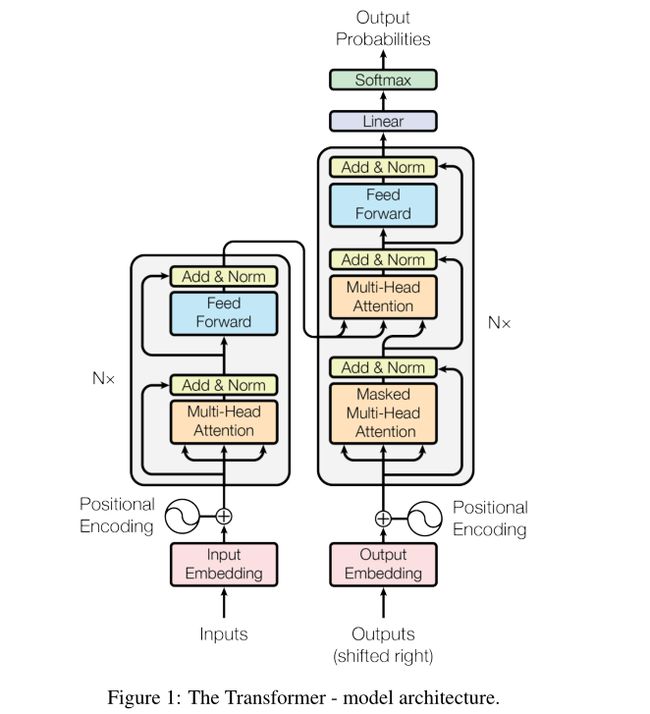
Encoder和Decoder
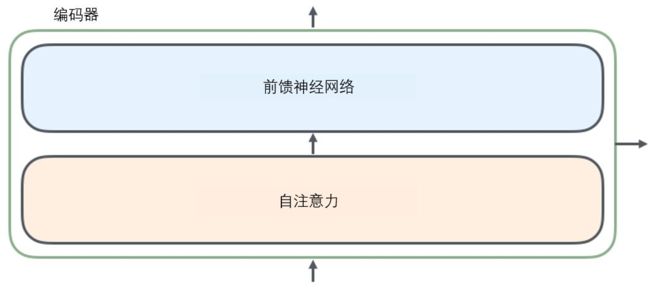
Encoder
Encoder由6个相同层的stack组成。每一层有两个子层。分别是是Multi-head Self-attention层和简单的fully connected前馈神经网络。在两个子层上使用残差连接[Add],然后是层归一化[Norm],[Add&Norm]都是用来加速模型的收敛速度,前者优化梯度消失问题,后者优化数据特征分布的稳定性。
也就是说,每个子层的输出是 L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x+ Sublayer(x)) LayerNorm(x+Sublayer(x)),其中 S u b l a y e r ( x ) Sublayer(x) Sublayer(x)是子层自身实现的函数。
为了方便这些剩余连接,model中的所有子层以及Embedding层都产生了 d m o d e l = 512 d_{model}= 512 dmodel=512的输出。
Decoder
Decoder也由6个相同层的stack组成。除每个encoder层中的两个子层外,decoder还插入第三个子层,该子层对encoder stack的输出执行Multi-head Self-attention。与encoder类似,我们在每个子层周围使用残差连接,然后进行层归一化。我们还修改了encoder stack中的Self-attention子层,以防止位置注意到后续位置。这种masking加上输出embedding被一个位置偏移的事实,确保了positionican的预测只依赖于小于i位置的已知输出。
Attention
一个attention function可以描述为将query和一组 key-value映射到输出,其中query、 key、value和输出都是向量。输出是作为value的加权和计算的,其中分配给每个value的权重是通过query与相应key的兼容性函数计算的。
Scaled Dot-Product Attention(单head的Self-attention)
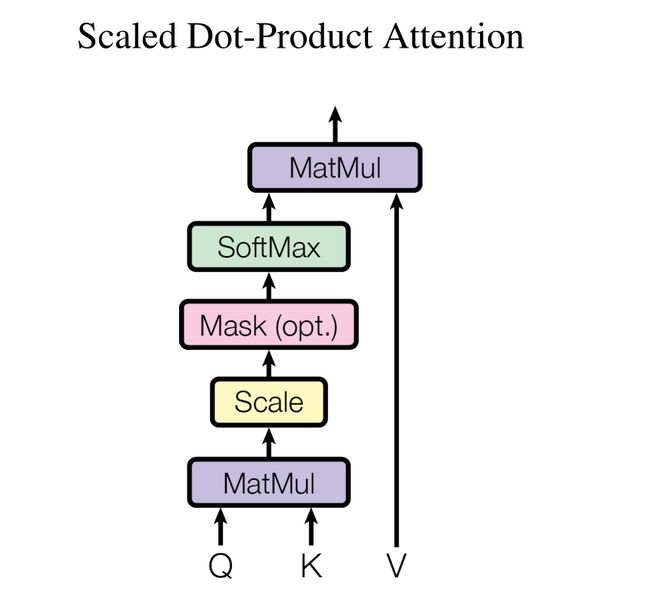
输出矩阵: A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d^k}})V Attention(Q,K,V)=softmax(dkQKT)V
下面结合李宏毅的视频详细讲解这个过程是怎么实现的:
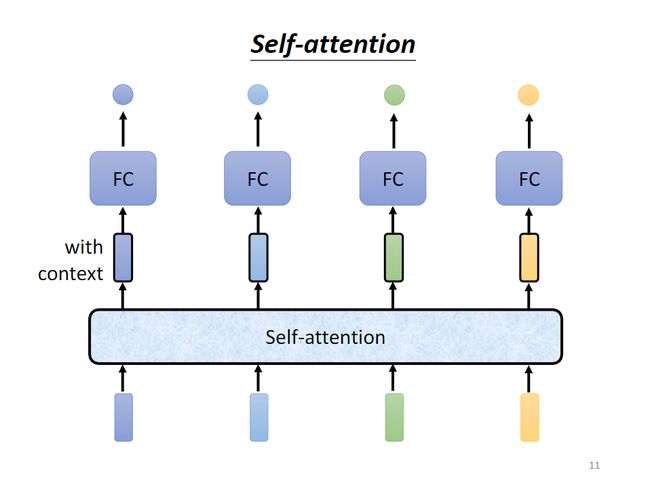
输入向量通过自注意力机制后,将输出考虑全局(with context)的向量

Self-attention和FC层可以多次叠加使用,Self-attention处理全局资讯,FC层处理某一个位置的资讯

对于输入 a i a^i ai,经过Self-attention层后,每一个输出 b i b^i bi都综合考虑了所有 a a a,即 a 1 a^1 a1到 a i a^i ai的信息。
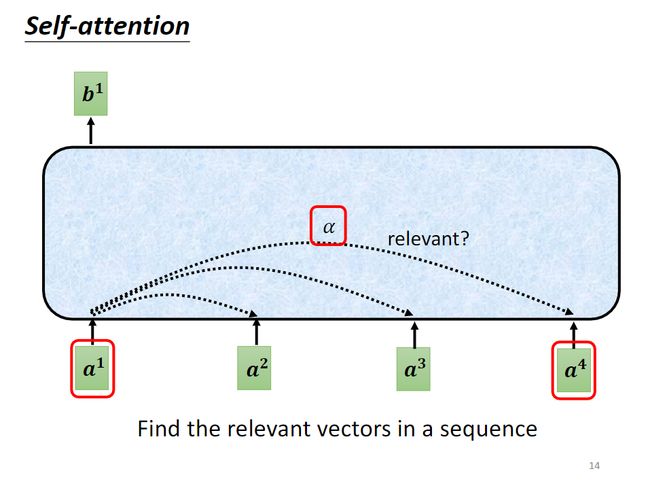
以 b 1 b^1 b1为例,要综合考虑 a 1 a^1 a1到 a i a^i ai的全部信息,就需要找出sequence中和 a 1 a^1 a1相关的向量。
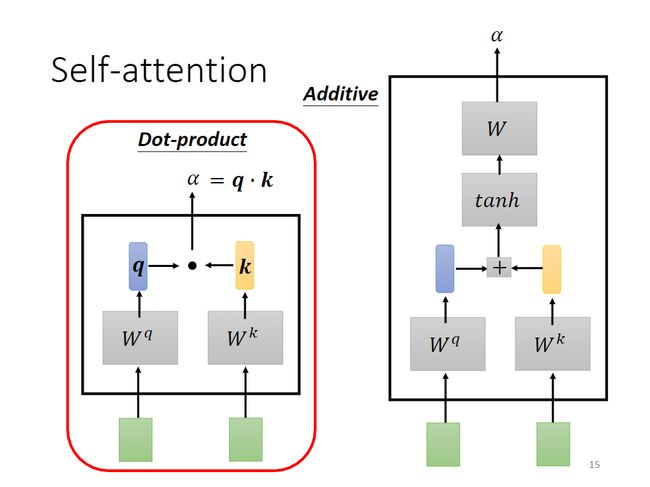
计算两个向量相关性的方法有很多种,Transformer中使用的是:输入的两个向量分别乘以两个矩阵 W q W^q Wq和 W k W^k Wk,得到向量 q q q和 k k k, α = q ⋅ k \alpha = q\cdot k α=q⋅k。

要计算向量 a 1 a^1 a1和向量 a 2 a^2 a2之间的关联,先把 a 1 a^1 a1乘以矩阵 W q W^q Wq得到 q 1 q^1 q1,然后把 a 2 a^2 a2乘以矩阵 W k W^k Wk得到 k 2 k^2 k2,这两个向量被分别叫做query向量和key向量,然后再将 q 1 q^1 q1和 k 2 k^2 k2点乘得到 α 1 , 2 \alpha_{1,2} α1,2, α 1 , 2 \alpha_{1,2} α1,2被称为attention score。
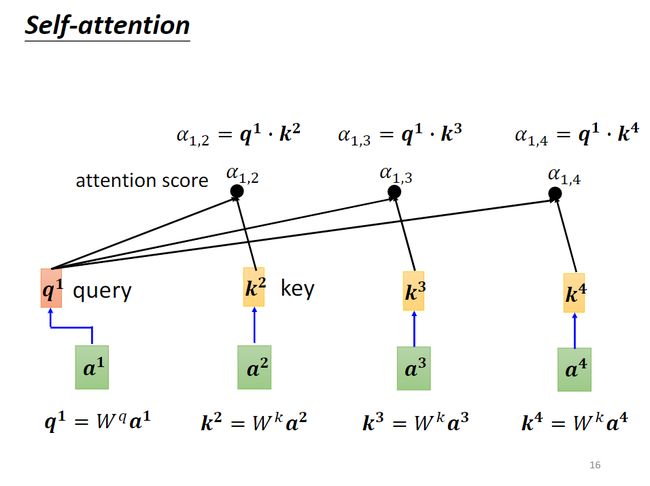
用同样的方法求出向量 a 1 a^1 a1和向量 a 3 a^3 a3之间的attention score,向量 a 1 a^1 a1和向量 a 4 a^4 a4之间的attention score,以及 a 1 a^1 a1和它自身之间的attention score。
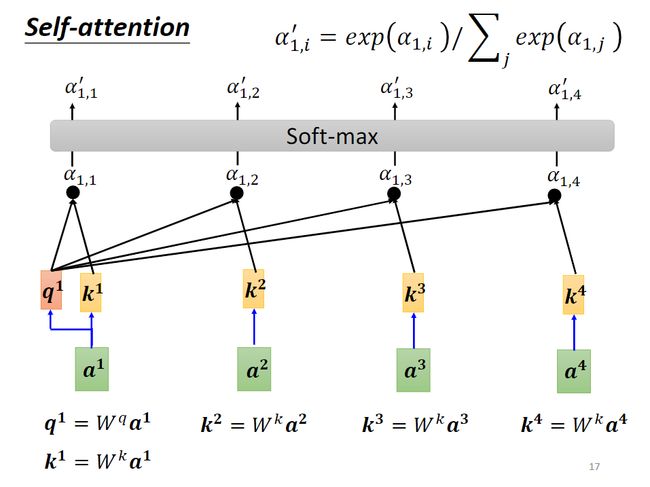
把求出来的 α i , j \alpha_{i,j} αi,j做softmax,转换成输出一个在0到1之间的数 α i , j ′ \alpha_{i,j}' αi,j′。
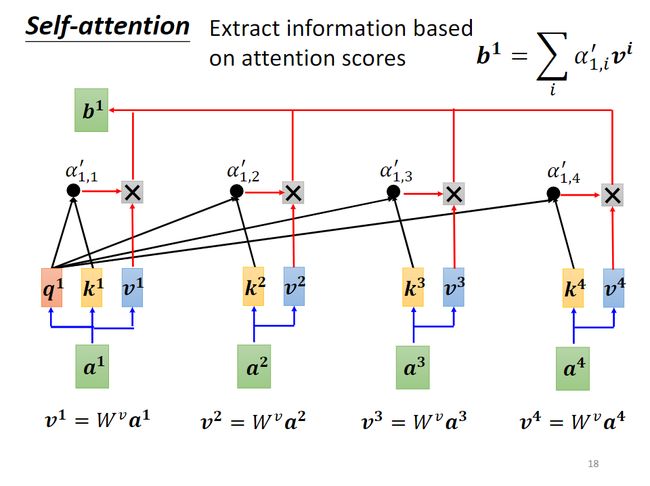
根据attention score抽取重要信息:把 a j a^j aj乘以矩阵 W v W^v Wv得到value向量 v j v^j vj,然后 α i , j ′ \alpha_{i,j}' αi,j′乘以对应向量 v j v^j vj,再累加求和得到输出 b i b^i bi,在 a j a^j aj中,谁的attention score越大,谁对最终 b i b^i bi的贡献也就越大,这样就达到了关注“最具有关联性的向量”的效果。
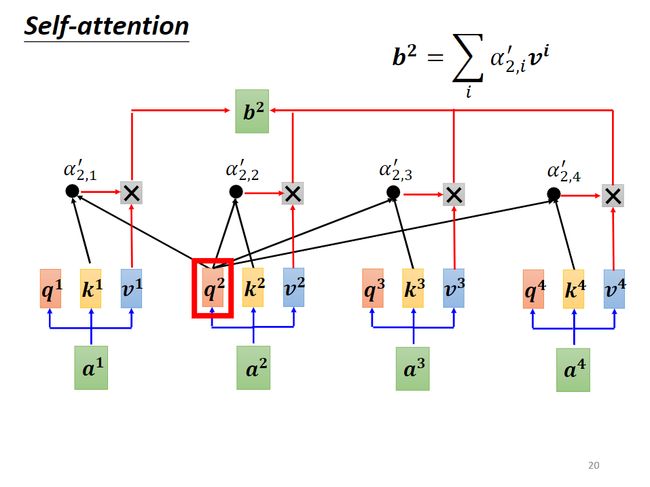
用同样的方法求出 b i , i ≠ 1 b^i,i\neq 1 bi,i=1,这个操作和求 b 1 b^1 b1是同时进行的,即并行操作,从矩阵的角度来看如下:

矩阵 W q W^q Wq乘以向量 a i a^i ai叠加起来的矩阵 I I I(可看作向量的向量 [ a 1 , a 2 , . . . , a j ] [a^1,a^2,...,a^j] [a1,a2,...,aj])得到矩阵 Q Q Q(可看作向量的向量 [ q 1 , q 2 , . . . , q j ] [q^1,q^2,...,q^j] [q1,q2,...,qj]);矩阵 W k W^k Wk乘以向量 a i a^i ai叠加起来的矩阵 I I I(可看作向量的向量 [ a 1 , a 2 , . . . , a j ] [a^1,a^2,...,a^j] [a1,a2,...,aj])得到矩阵 K K K(可看作向量的向量 [ k 1 , k 2 , . . . , k j ] [k^1,k^2,...,k^j] [k1,k2,...,kj]);矩阵 W v W^v Wv乘以向量 a i a^i ai叠加起来的矩阵 I I I(可看作向量的向量 [ a 1 , a 2 , . . . , a j ] [a^1,a^2,...,a^j] [a1,a2,...,aj])得到矩阵 V V V(可看作向量的向量 [ v 1 , v 2 , . . . , v j ] [v^1,v^2,...,v^j] [v1,v2,...,vj])
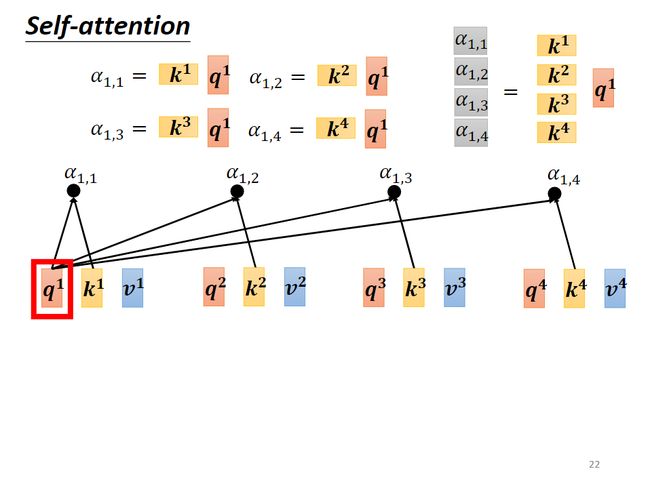
求attention score的过程其实就是向量 q q q和 k k k点乘,那么求 a 1 a^1 a1对 a i , i ≠ 1 a^i,i\neq 1 ai,i=1的attention score的过程就是矩阵 K T K^T KT( [ k 1 , k 2 , . . . , k j ] T [k^1,k^2,...,k^j]^T [k1,k2,...,kj]T)和向量 q 1 q^1 q1做乘法,得到向量 [ a 1 , 1 , a 1 , 2 , . . . , a 1 , j ] T [a^{1,1},a^{1,2},...,a^{1,j}]^T [a1,1,a1,2,...,a1,j]T。
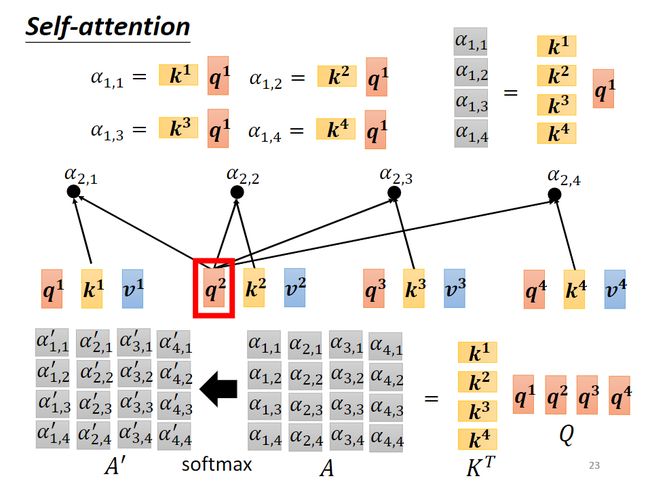
求所有向量的attention score,这个过程的矩阵化表述就是MatMul: A = K T ⋅ Q A=K^T\cdot Q A=KT⋅Q,SoftMax: A ′ = s o f t m a x ( A ) A'=softmax(A) A′=softmax(A),在Transformer中,还有Scale: A = A / d k A = A/\sqrt{d_k} A=A/dk,用来抵消点积大小变大对SoftMax的影响。
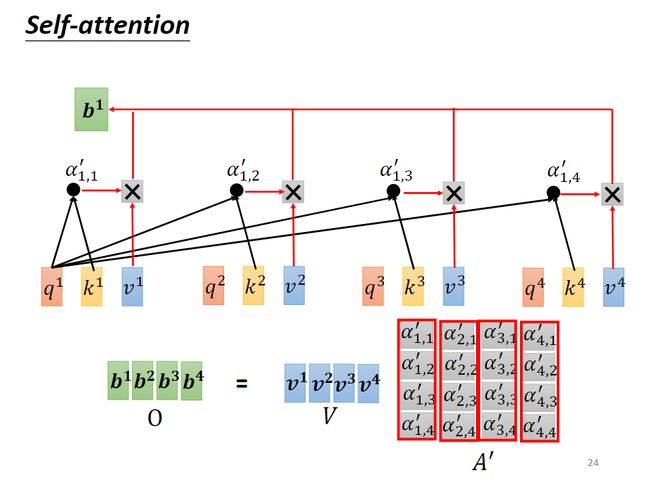
attention score矩阵再乘以value矩阵 V V V,最终的输出矩阵 O O O为MatMul: O = V ⋅ A ′ O=V\cdot A' O=V⋅A′。
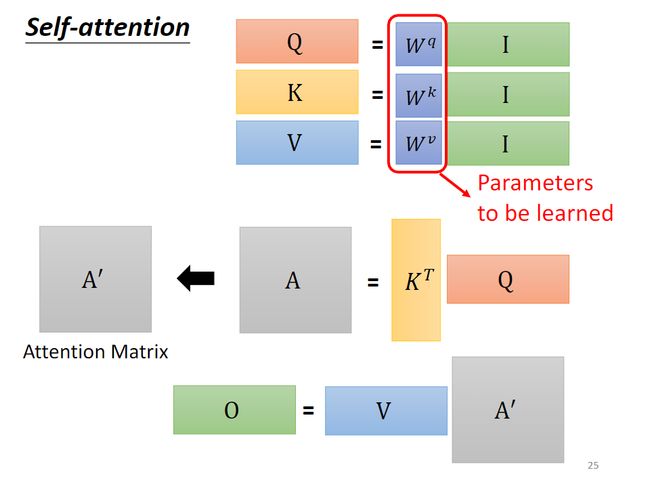
上述过程其实本质就是一连串的矩阵乘法,在这个过程中,只有三个权重矩阵 W q W^q Wq、 W k W^k Wk、 W v W^v Wv是需要训练学习的。
Multi-Head Attention
在计算Self-attention的时候,我们只是找了向量之间一种相关的形式,但是现实是向量之间可能存在多种相关的形式,所以引入Multi-head Self-attention,Multi-head Self-attention使得模型能够在不同位置共同关注来自不同表示子空间的信息。
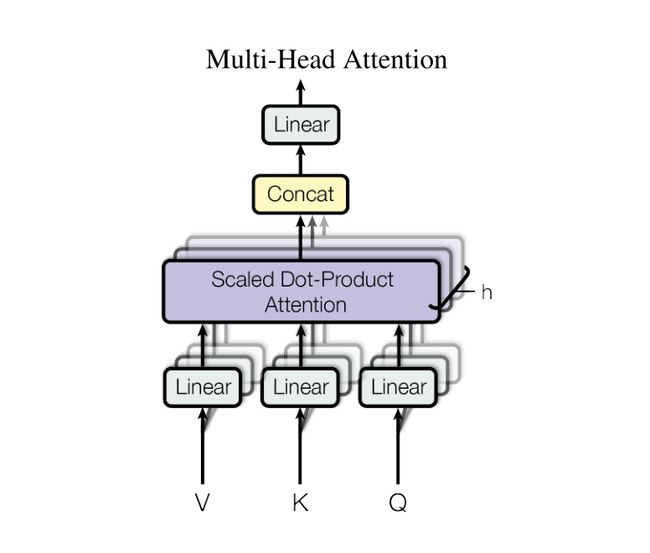
输出矩阵:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , h e a d 2 , . . . , h e a d h ) W O MultiHead(Q,K,V)=Concat(head_1,head_2,...,head_h)W^O MultiHead(Q,K,V)=Concat(head1,head2,...,headh)WO
w h e r e h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) where\ head_i=Attention(QW_i^Q,KW_i^K,VW_i^V) where headi=Attention(QWiQ,KWiK,VWiV)
其中 W i Q ∈ R d m o d e l × d k W_i^Q\in \mathbb{R}^{d_{model}\times d_k} WiQ∈Rdmodel×dk, W i K ∈ R d m o d e l × d k W_i^K\in \mathbb{R}^{d_{model}\times d_k} WiK∈Rdmodel×dk, W i V ∈ R d m o d e l × d v W_i^V\in \mathbb{R}^{d_{model}\times d_v} WiV∈Rdmodel×dv, W i O ∈ R h d v × d m o d e l W_i^O\in \mathbb{R}^{hd_v\times d_model} WiO∈Rhdv×dmodel
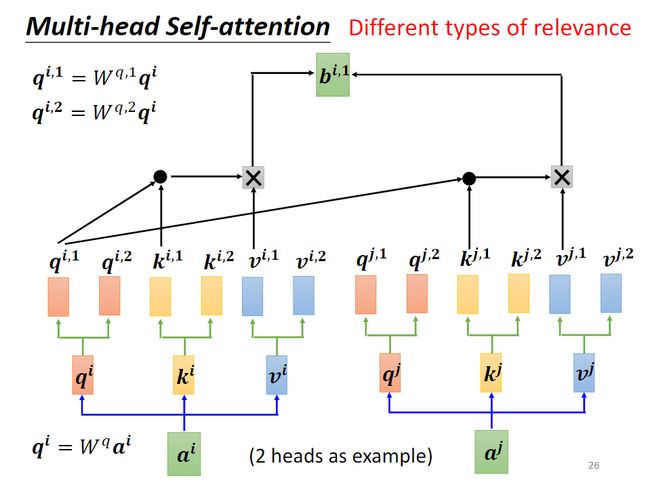
以两个head为例,把向量 q q q、 k k k、 v v v分别再乘以两个矩阵,得到对应的向量 q i , m q^{i,m} qi,m、 q j , n q^{j,n} qj,n、 k i , m k^{i,m} ki,m、 k j , n k^{j,n} kj,n、 v i , m v^{i,m} vi,m、 v j , n v^{j,n} vj,n,这是为了用两种head找出对应的两种不同的相关性,然后计算过程和前述相同,但是每一个head只计算一条支路的对应输出结果 b i , m b^{i,m} bi,m。
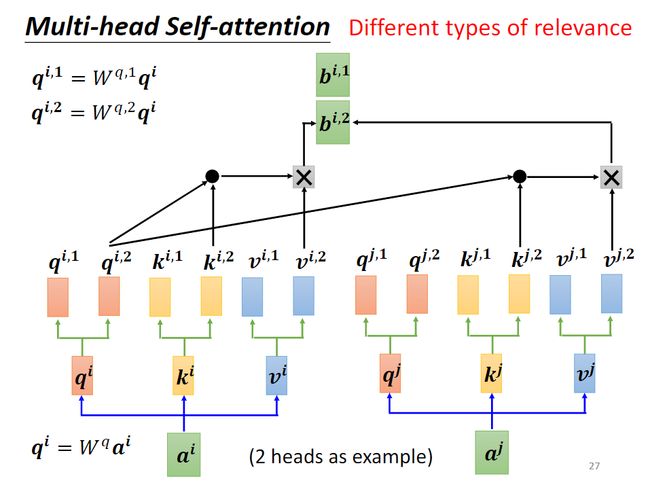
计算完以后,把多个 b i , m b^{i,m} bi,m接起来作为一个矩阵。
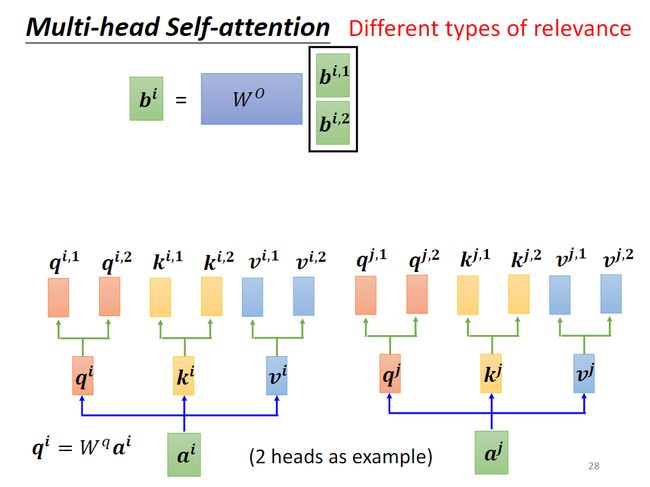
用权重矩阵 W O W^O WO乘以这个矩阵来得到最终的输出 b i b^i bi。这是以2 head为例的情况,在transformer中一般使用8个head。
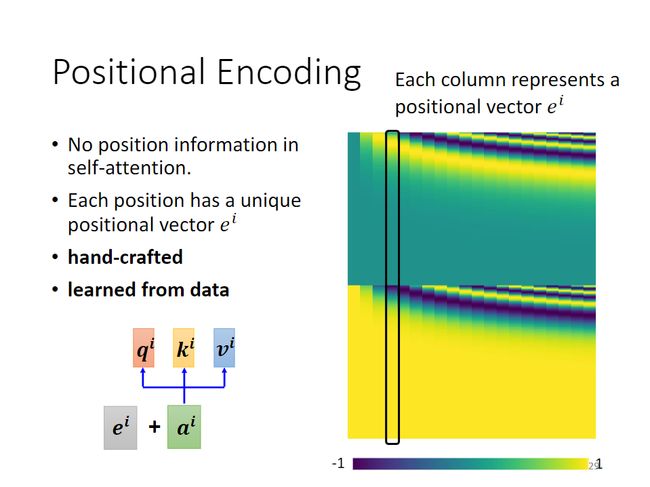
但是在前述计算Self-attention的过程中,忽略了一个也许很重要的资讯——位置资讯,因此,为位置设定一个向量 e i e^i ei并加到 a i a^i ai上面,这就是Positional Encoding。
Position-wise Feed-Forward Networks
结构非常简单,由线性变换组成,中间有一个ReLU激活。
F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0,xW_1+b_1)W_2+b2 FFN(x)=max(0,xW1+b1)W2+b2

CNN是受限的Self-attention,Self-attention是具有可以被学习的感受野的CNN,已经有论文(【On the Relationship between Self-Attention and Convolutional Layers】)证明,只要合理设定Self-attention的四个参数,就可以达到和CNN完全相同的效果。
参考:
- 图解Transformer(完整版)
- 台大李宏毅21年机器学习课程 self-attention和transformer
- Transformer论文逐段精读【论文精读】
Vision TransFormer架构的学习
Paper:《An Image is Worth 16x16 Words:Transformers for Image Recognition at Scale》
Where:ICLR 2021
本周初步学习了CV的TransFormer:Vision Transformer(ViT)。
论文背景:
CNN具有对全局特征把握不好的缺点,卷积得到的feature map是局部敏感的,对局部特征提取的很好,但是难以整合全局特征。Attention可以更好的关注全局特征,但在CV领域,Attention要么和CNN一起应用,要么在保证总结构不变的情况下用于替换CNN中的某些组件。
创新点:
Transformer完全舍弃卷积架构而使用纯Attention架构,Transformer的并行化处理相比CNN的串行化处理,可以在同一时间分析图像中的所有特征,考虑任意两个特征之间的相互关系,且不受它们在图片中位置的影响。论文直接把standard Transformer迁移到CV,架构基本没有改变,而是把图片输入处理为standard Transformer的输入形式。
论文结构:
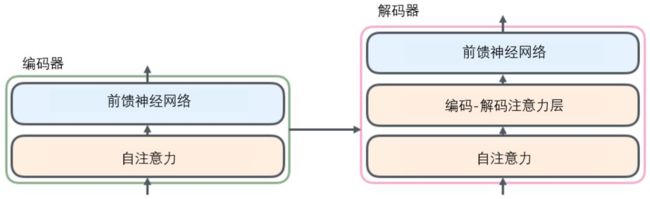
transformer由编码组件(encoders)和解码组件(decoders)组成,Encoders将输入数据转换成一种不同的表示,而Decoders将这个新的表示转换回原来的形式。
期望:输入数据经过Encoder和Decoder后:
- 尽可能多地保留信息
- 新的表示有各种好的特性
但是standard Transformer的输入形式是1维的token,而图片是二维的,所以需要先把原始图片进行分块展平的处理:
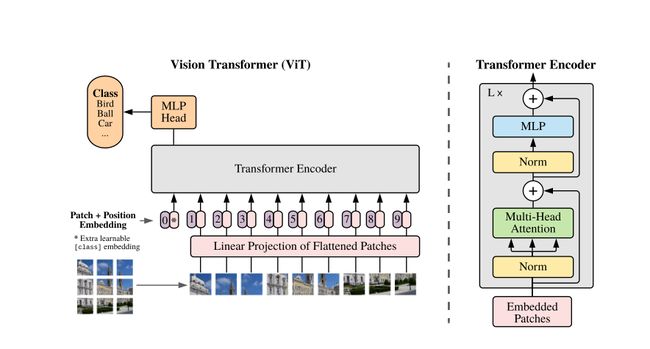
对于原始维度为 H × W × C H\times W\times C H×W×C的图像 x x x,将其分割为 P × P P\times P P×P大小的patch,分割数量为 N = H W p 2 N=\frac{HW}{p^2} N=p2HW,对每个patch展平为长为 P 2 × C P^2\times C P2×C的一维向量,图片转变成a sequence of patchs: x p ∈ R N × ( P 2 ⋅ C ) x_p\in \mathbb{R}^{N\times(P^2\cdot C)} xp∈RN×(P2⋅C),然后是Patch Embedding,具体操作是用全连接层把向量维度映射为D, x p ′ ∈ R N × D x_p' \in \mathbb{R}^{N\times D} xp′∈RN×D。
原始的Transformer引入了一个 Positional encoding 来加入序列的位置信息,ViT同样也引入了pos_embedding,是用一个可训练的变量替代。
传统的Transformer采取的是类似seq2seq编解码的结构 而ViT只用到了Encoder编码器结构,缺少了解码的过程,因此这里ViT设置了额外的一个用于分类的向量,与输入进行拼接。同样这是一个可学习的变量。
参考:
- [翻译]AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE
- Attention(注意力)机制
- 【论文笔记】An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale(Vision Transformer, ViT)
- 初识 CV Transformer 之《ViT》论文精读
- 一张图等于 16x16 个字,计算机视觉也用上 Transformer 了
- 【CV】Transformer学习笔记
Swin Transformer
Paper:《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》
Where:2021.3.25 arxiv
论文背景:
Transformer 从 NLP 到 CV 到难点在于,与文本中的单词相比,视觉实体的规模和图像像素的高分辨率有很大的变化。论文提出一种新的 Transformer backbone取代传统CNN,让Transformer成为CV领域新的通用结构。
创新点:
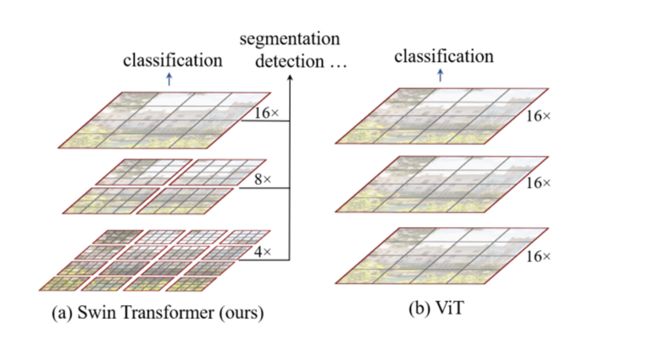
提出了一种层级 Transformer,其表示是通过移动窗口计算的:
- 移位窗口优点:通过将自注意计算限制在不重叠的局部窗口上,同时允许跨窗口连接,从而带来更高的效率。
- 层次结构优点:具有在不同尺度上建模的灵活性,并具有与图像大小相关的线性计算复杂性。
Swin Transformer是一个多阶段的网络框架,而且每一个阶段的输出也是一组Feature Map,因此可以非常方便的将其迁移到几乎所有CV任务中。
论文结构:
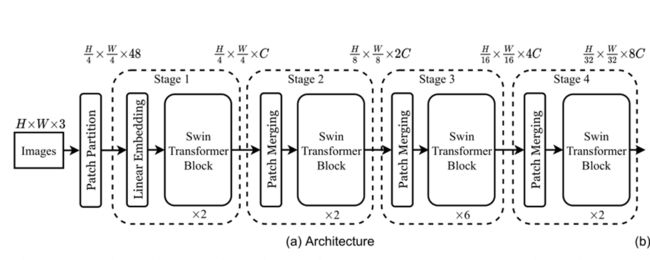
以最轻量的网络Swin-T为例,网络架构如下:
架构分析
输入图片是 H × W × 3 H\times W\times 3 H×W×3的图片,首先经过Patch Partition被分割成 H 4 × W 4 × 48 \frac{H}{4} \times \frac{W}{4}\times 48 4H×4W×48的图片.:
首先,图片被分割成 H 4 × W 4 \frac{H}{4}\times \frac{W}{4} 4H×4W个patch,每个patch大小是 4 × 4 4\times 4 4×4,被称为一个token。这些patch,每一个patch被展开后的特征维度是 4 × 4 × 3 = 48 4\times 4\times 3=48 4×4×3=48,其中4是patch size,3是RGB通道数量,如下图:

然后 H 4 × W 4 × 48 \frac{H}{4}\times \frac{W}{4}\times 48 4H×4W×48的feature map经过一个被称为Linear Embedding的FC layer后,被投影到任意维度(记为C) H 4 × W 4 × C \frac{H}{4}\times \frac{W}{4}\times C 4H×4W×C,然后经过Swin Transformer Block得到计算过Self-attention的feature map,这个阶段被称为Stage 1.
后面三个Stage架构一样,和Stage 1比起来是将Partition和Stage 1里面的Linear Embedding合并为Patch Merging操作,每经过一个Stage,feature map的H和W都会缩小为 1 2 \frac{1}{2} 21,通道数量增加为原来的2倍: H 4 × W 4 × C \frac{H}{4}\times \frac{W}{4}\times C 4H×4W×C的feature map经过Stage 2后变为 H 8 × W 8 × 2 C \frac{H}{8}\times \frac{W}{8}\times 2C 8H×8W×2C的feature map,再经过Stage 3后变为 H 16 × W 16 × 4 C \frac{H}{16}\times \frac{W}{16}\times 4C 16H×16W×4C的feature map,最后经过Stage 4变为 H 32 × W 32 × 8 C \frac{H}{32}\times \frac{W}{32}\times 8C 32H×32W×8C的feature map。
Patch Merging
Patch Merging是先做一个类似下采样的操作,采样的filter size和stride都设置为2(和Patch Partition做的是一样的操作,只不过Patch Partition的filter size和stride设置为patch size即4),这样一个 2 × 2 2\times 2 2×2大小的区域有4个token,Merge的第一步就是把这四个token拼接为一个token,拼接后的token是 1 × 1 × 4 C 1\times 1 \times 4C 1×1×4C(C为原来token的通道数),新的token的receptive filed是原本的4倍,所以原本为 a × b × C a\times b\times C a×b×C的feature map在下采样和拼接后变为 a 2 × b 2 × 4 C \frac{a}{2}\times \frac{b}{2}\times 4C 2a×2b×4C,然后再经过Linear Embedding把通道数缩小一半,变为 a 2 × b 2 × 2 C \frac{a}{2}\times \frac{b}{2}\times 2C 2a×2b×2C:
Swin Transformer Block
Swin Transformer Block必然是偶数个,因为block在使用时是两个一起使用的:
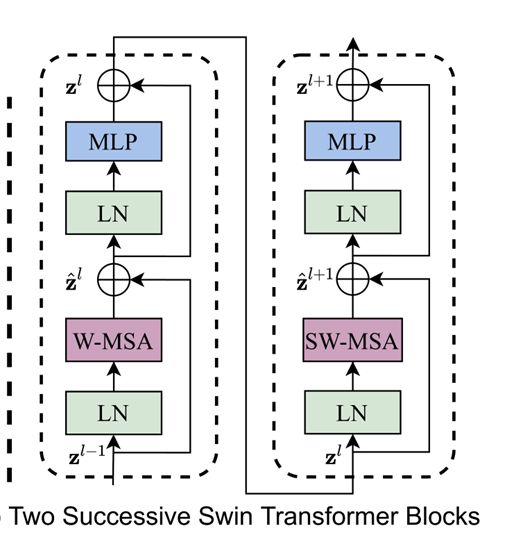
两个先后使用的block的区别仅为:前一个block里使用W-MSA(Window-MultiHead Self-attention),后一个block使用的是SW-MSA(Shifted Window-MultiHead Self-attention)。feature map输入前一个block后先经过LN层进行正则化,然后被输入MSA,在窗口里计算Self-attention,然后加上前一次层的残差连接得到一个中间状态;中间状态经过LN层正则化,然后经过作为前馈网络的MLP,再加上中间状态的残差连接得到block的输出。这个输出作为后一个block的输入。
z ^ l = W-MSA ( L N ( z l − 1 ) ) + z l − 1 \hat{z}^l=\text{W-MSA}(LN(z^{l-1}))+z^{l-1} z^l=W-MSA(LN(zl−1))+zl−1 z l = M L P ( L N ( z ^ l ) ) + z ^ l z^l=MLP(LN(\hat{z}^l))+\hat{z}^l zl=MLP(LN(z^l))+z^l z ^ l + 1 = SW-MSA ( L N ( z l ) ) + z l \hat{z}^{l+1}=\text{SW-MSA}(LN(z^l))+z^l z^l+1=SW-MSA(LN(zl))+zl z l + 1 = M L P ( L N ( z ^ l + 1 ) ) + z ^ l + 1 z^{l+1}=MLP(LN(\hat{z}^{l+1}))+\hat{z}^{l+1} zl+1=MLP(LN(z^l+1))+z^l+1
W-MSA
W-MSA \text{W-MSA} W-MSA是以窗口为单位进行特征匹配的,因此使用相对位置编码,相对位置编码的范围也应该是以窗口为单位(它不是Swin Transformer提出的):
Z = s o f t m a x ( Q K T d k + B ) V Z=softmax(\frac{QK^T}{\sqrt{d_k}}+B)V Z=softmax(dkQKT+B)V
ViT的MSA是在全局上计算自注意力的,即Window大小等于输入图片大小,这样做patch数量是不固定的,显然图片增大时,patch的数量平方增大;Swin Transformer划定窗口,每个窗口的patch数量固定,在每个窗口上计算Self-attention,把计算Self-attention的窗口复杂度从平方降到了线性。
假设每个Window包含 M × M M\times M M×M个patch( M M M是Window大小),每个patch是 h × w h\times w h×w,当 M 固定时 (默认设置为7),MSA的复杂度是 patch 个数 h w hw hw 的二次方,W-MSA是线性的:
Ω ( M S A ) = 4 h w C 2 + 2 ( h w ) 2 C \Omega(MSA)=4hwC^2+2(hw)^2C Ω(MSA)=4hwC2+2(hw)2C Ω ( W-MSA ) = 4 h w C 2 + 2 M 2 h w C \Omega(\text{W-MSA})=4hwC^2+2M^2hwC Ω(W-MSA)=4hwC2+2M2hwC
解释:
- Q = x × W Q Q=x\times W^Q Q=x×WQ、 K = x × W K K=x\times W^K K=x×WK、 V = x × W V V=x\times W^V V=x×WV, x x x的维度是 ( h w , C ) (hw,C) (hw,C), W W W的维度是(C,C),所以计算 Q , K , V Q,K,V Q,K,V的复杂度是 3 h w C 2 3hwC^2 3hwC2;
- Q , K , V Q,K,V Q,K,V的维度均是 ( h w , C ) (hw,C) (hw,C),计算 Q K T QK^T QKT的复杂度是 ( h w ) 2 C (hw)^2C (hw)2C
- softmax后 Q K T QK^T QKT乘 V V V得到 Z Z Z, Q K T QK^T QKT的维度是 ( h w , h w ) (hw,hw) (hw,hw),复杂度是 ( h w ) 2 C (hw)^2C (hw)2C
- Z Z Z乘 W Z W^Z WZ的复杂度是 h w C 2 hwC^2 hwC2
W-MSA \text{W-MSA} W-MSA在窗口内计算Self-attention,因此 2 ( h w ) 2 C 2(hw)^2C 2(hw)2C变为 2 M 2 h w C 2M^2hwC 2M2hwC。
SW-MSA
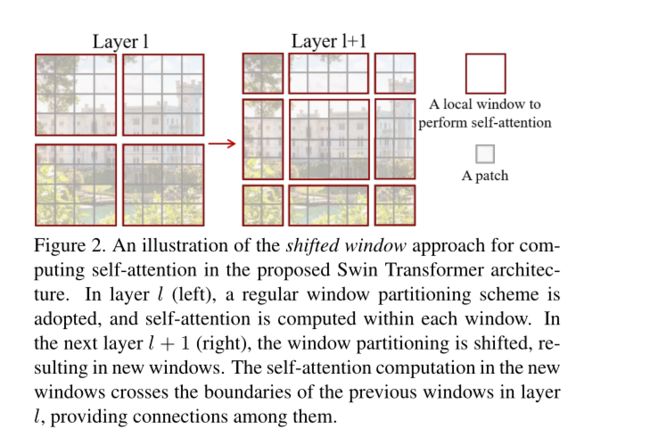
将每个窗口当做一个独立区域计算,会忽略了窗口之间交互的必要性,所以论文提出了Shifted Window,这也是论文的精华所在。
左图是Local Window,在 8 × 8 的 8\times 8的 8×8的feature map上均匀划分 2 × 2 2\times 2 2×2个 4 × 4 4\times 4 4×4patch size大小的Window(M=4),右图是Shifted Window,在Local Window的配置上,每个窗口向右移 ⌊ M 2 ⌋ \lfloor \frac{M}{2} \rfloor ⌊2M⌋个patch,向下移 ⌊ M 2 ⌋ \lfloor \frac{M}{2} \rfloor ⌊2M⌋个patch(图例是移动了2个patch)。
Shifted Window存在的问题:Window增多,由原本 ⌈ h M ⌉ × ⌈ w M ⌉ \lceil \frac{h}{M} \rceil \times \lceil \frac{w}{M} \rceil ⌈Mh⌉×⌈Mw⌉个Window变成了 ( ⌈ h M ⌉ + 1 ) × ( ⌈ w M ⌉ + 1 ) (\lceil \frac{h}{M} \rceil+1) \times (\lceil \frac{w}{M} \rceil+1) (⌈Mh⌉+1)×(⌈Mw⌉+1)个Window
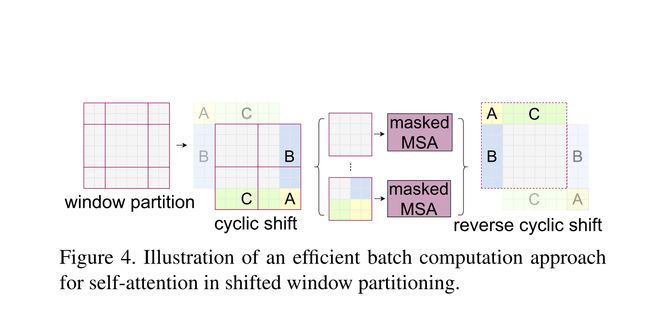
特征图移位
Swin Transformer通过一种巧妙的方法:特征图移位,并给Attention设置mask来实现Shifted Window和Local Window个数下计算结果等价的算法。
特征图移位操作通过torch.roll()函数实现:
torch.roll(input, shifts, dims=None) → Tensor
- input (Tensor) —— 输入张量
- shifts (python:int 或 tuple of python:int) —— 张量元素移位的位数。如果该参数是一个元组(例如shifts=(x,y)),dims必须是一个相同大小的元组(例如dims=(a,b)),相当于在第a维度移x位,在b维度移y位
- dims (int 或 tuple of python:int) 确定的维度
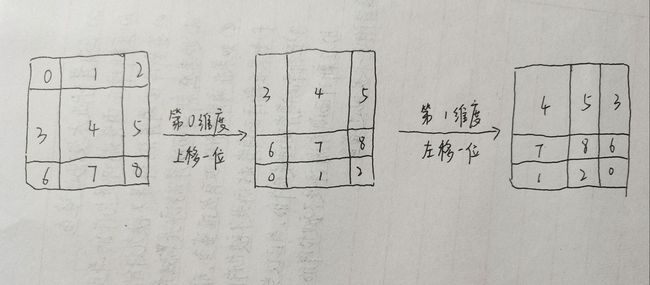
我们想要让左图roll到右图:
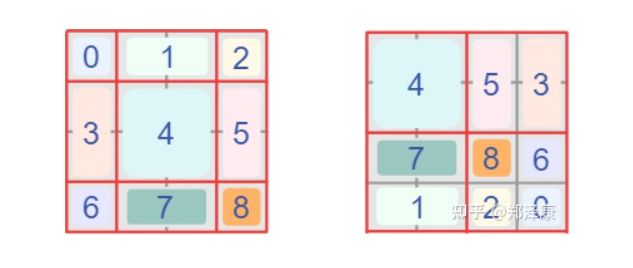
这个操作是:torch.roll(x, shifts=(-1, -1), dims=(0, 1))
x = torch.tensor([[0, 1, 1, 2], [3, 4, 4, 5], [3, 4, 4, 5], [6, 7, 7, 8]])
print(x)
这是模拟创建的张量x:
tensor([[0, 1, 1, 2],
[3, 4, 4, 5],
[3, 4, 4, 5],
[6, 7, 7, 8]])
第一步,第0维度上移一位:
x = torch.roll(x, -1, 0)
print(x)
tensor([[3, 4, 4, 5],
[3, 4, 4, 5],
[6, 7, 7, 8],
[0, 1, 1, 2]])
第二步,第1维度上移一位:
x = torch.roll(x, -1, 1)
print(x)
tensor([[4, 4, 5, 3],
[4, 4, 5, 3],
[7, 7, 8, 6],
[1, 1, 2, 0]])
这样,就把 ( ⌈ h M ⌉ + 1 ) × ( ⌈ w M ⌉ + 1 ) (\lceil \frac{h}{M} \rceil+1) \times (\lceil \frac{w}{M} \rceil+1) (⌈Mh⌉+1)×(⌈Mw⌉+1)个Window(上例为9个Window)变回了 ⌈ h M ⌉ × ⌈ w M ⌉ \lceil \frac{h}{M} \rceil \times \lceil \frac{w}{M} \rceil ⌈Mh⌉×⌈Mw⌉个Window(上例为4个Window)。
mask是其实就是让不对应的q和k的attention score被忽略掉,只保留对应的q和k的attention score,这个操作通过给attention score加上0和Inf组成的二值矩阵来实现:
对于移位后的Window,通过给Attention作mask的方法让特征图移位后的计算结果和移位前一致:

把没有数字的格子都做mask,这样最后计算结果才是q和k一致的attention score
tensor([[[[[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]]],
[[[ 0., -100., 0., -100.],
[-100., 0., -100., 0.],
[ 0., -100., 0., -100.],
[-100., 0., -100., 0.]]],
[[[ 0., 0., -100., -100.],
[ 0., 0., -100., -100.],
[-100., -100., 0., 0.],
[-100., -100., 0., 0.]]],
[[[ 0., -100., -100., -100.],
[-100., 0., -100., -100.],
[-100., -100., 0., -100.],
[-100., -100., -100., 0.]]]]])
把这样一个tensor作为mask加到attention的计算结果,并进行softmax。mask的值理论上应该设置为无穷大,但是实际设置为-100,softmax后就会忽略掉对应的值。
最终输出层
在经过Stage 4后,Swin Transformer先通过一个Global Average Pooling得到一个特征向量,再通过一个LN和一个全连接得到最终的预测结果:
y ^ = M L P ( L N ( G A P ( z 4 ) ) ) \hat{y}=MLP(LN(GAP(z^4))) y^=MLP(LN(GAP(z4)))
Swin Transformer家族
论文提出了四种Swin Transformer,它们的区别在于Stage 1隐层节点的长度,每个stage的层数,多头自注意力机制的头的个数:
| model | 隐层节点长度 | Stage层数 | MSA的head个数 |
|---|---|---|---|
| Swin-T | 96 | (2,2,6,2) | (3,6,12,24) |
| Swin-S | 96 | (2,2,18,2) | (3,6,12,24) |
| Swin-B | 128 | (2,2,18,2) | (4,8,16,32) |
| Swin-L | 192 | (2,2,18,2) | (6,12,24,48) |
参考:
CV+Transformer之Swin Transformer
图解Swin Transformer
MyDLNote-Transformer: Swin Transformer, 使用移位窗口的分层 Vision Transformer