数学建模学习笔记（六）——多元线性回归分析
文章目录
-
- 一、综述
- 二、常见的回归分析
- 三、对于相关性的理解
- 四、一元线性回归模型
- 五、对于回归系数的解释
- 六、内生性
- 七、四类线性模型回归系数的解释
- 八、对于定性变量的处理——虚拟变量 X X X
- 九、下面来看一个实例
- 十、扰动项需要满足的条件
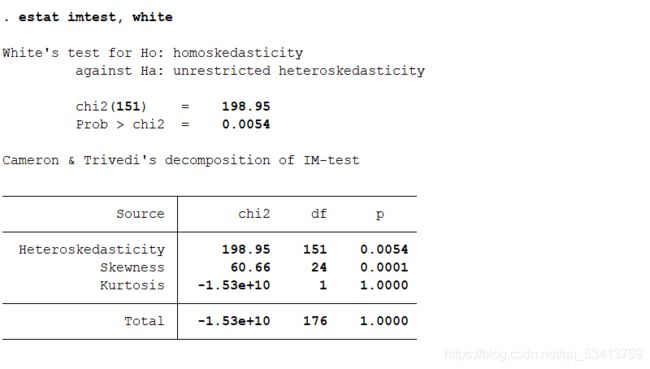
- 十一、异方差
- 十二、多重共线性
- 十三、逐步回归
- 十四、总结
一、综述
无论是什么回归模型，它们的基本任务都是通过研究自变量 x x x 和因变量 y y y 的相关关系，从而形成能够解释 y y y 的变化的方法，进而能够通过自变量 x x x 去预测因变量 y y y 。
回归分析的基本任务：
- 变量选择：确定重要变量
- 判断是正相关还是负相关
- 估计回归系数
二、常见的回归分析
常见的回归分析有： { 线 性 回 归 0 − 1 回 归 定 序 回 归 计 数 回 归 生 存 回 归 \left\{ \begin{aligned} &线性回归 \\ &0 - 1回归 \\ &定序回归 \\ &计数回归 \\ &生存回归 \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧线性回归0−1回归定序回归计数回归生存回归，文章只从线性回归的角度来阐述线性回归分析用于解决问题的策略和步骤。它们的区别是因为因变量 y y y 的不同而引起的。
| 因变量 y y y | |
|---|---|
| 线性回归 | y y y 为连续型的数值变量，例如：家庭收入逐年增加 ⋯ \cdots ⋯ |
| 0 - 1回归 | y y y 的结果可以抽象为0或者1（类似于计算机中的二进制0和1），例如：喜欢和不喜欢 ⋯ \cdots ⋯ |
| 定序回归 | y y y 为表示等级或者程度的变量（具有一定的顺序大小） ⋯ \cdots ⋯ |
| 计数回归 | y y y 为计数变量，例如：抛硬币次数的增加 ⋯ \cdots ⋯ |
| 生存回归 | y y y 为阶段的数据，例如：研究某一因素对于年龄的影响，便可以截取一个年龄段，满足该年龄段的人进行计数即可 |
三、对于相关性的理解
相关性 ≠ \neq = 因果性
即不能从相关性的结果分析中让两个变脸拥有绝对的因果关系。
四、一元线性回归模型
假设 x x x 是自变量， y y y 是因变量，且满足如下线性关系： y i = β 0 + β 1 x i + μ i y_i = \beta_0 + \beta_1x_i + \mu_i yi=β0+β1xi+μi β 0 \beta_0 β0 和 β 1 \beta_1 β1 为回归系数， μ i \mu_i μi 为无法观测的且满足一定条件的扰动项$
令预测值 y i ^ = β 0 ^ + β 1 ^ x i \hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i yi^=β0^+β1^xi
其中 β 0 ^ , β 1 ^ = a r g β 0 , β 1 m i n ( ∑ i = 1 n ( y i − y i ^ ) 2 ) = a r g β 0 , β 1 m i n ( ∑ i = 1 n ( y i − β 0 ^ − β i ^ x i ) 2 ) \hat{\beta_0}, \hat{\beta_1} = arg_{\beta_0, \beta_1}min(\sum_{i=1}^{n}(y_i - \hat{y_i})^2) \\ \\ = arg_{\beta_0, \beta_1}min(\sum_{i=1}^{n}(y_i - \hat{\beta_0} - \hat{\beta_i}x_i)^2) β0^,β1^=argβ0,β1min(∑i=1n(yi−yi^)2)=argβ0,β1min(∑i=1n(yi−β0^−βi^xi)2)
β 0 ^ , β 1 ^ = a r g β 0 , β 1 m i n ( ∑ i = 1 n ( μ i ^ ) 2 ) \hat{\beta_0}, \hat{\beta_1} = arg_{\beta_0, \beta_1}min(\sum_{i=1}^{n}(\hat{\mu_i})^2) β0^,β1^=argβ0,β1min(∑i=1n(μi^)2)
五、对于回归系数的解释
y i = β 0 + β 1 x 1 i + β 2 x 2 i + μ i , β 0 和 β 1 为回归系数 y_i = \beta_0 + \beta_1x_{1i} + \beta_2x_{2i} + \mu_i,\beta_0 \text{和} \beta_1 \text{为回归系数} yi=β0+β1x1i+β2x2i+μi,β0和β1为回归系数
β 0 \beta_0 β0：在 x 1 x_1 x1 和 x 2 x_2 x2 都为0时， y y y 的平均值为 β 0 \beta_0 β0
β 1 \beta_1 β1：在保持其他变量不变的情况下， x 1 i x_{1i} x1i 每增加一个单位， y y y 的平均值增加 β 0 \beta_0 β0
β 2 \beta_2 β2：在保持其他变量不变的情况下， x 2 i x_{2i} x2i 每增加一个单位， y y y 的平均值增加 β 1 \beta_1 β1
注意：每引入一个自变量，对于每个自变量前面的回归系数影响都是非常大的。因此在求回归方程的时候，尽量不要遗漏变量，否则会导致内生性的问题。
六、内生性
由于 μ \mu μ 是一个满足条件但却无法观测的扰动项，因此 μ \mu μ 和自变量们是否相关会导致回归系数的准确与否。
- 若 μ \mu μ 与自变量们均不相关，则称该回归模型具有外生性。
- 若 μ \mu μ 与自变量们相关，则称该回归模型具有内生性。
由于要求 μ \mu μ 与自变量们都不相关，此条件要求太强。因此，我们可以将方程中的自变量分为核心变量和控制变量两类（顾名思义，核心变量：最需要进行估计的变量；控制变量：对变量本身无太大兴趣，但将之加入方程是为了避免内生性）。
在实际应用中，我们只需要保持核心变量与 μ \mu μ 不相关即可
七、四类线性模型回归系数的解释
在平常的模型分析中，我们也可以通过代换，将取对数的变量做代换，同样可以达到线性的目的。
-
一元线性回归： y = a + b x + μ y = a + bx + \mu y=a+bx+μ
x x x 每增加一个单位， y y y 平均变化 b b b 个单位。 -
双对数模型： ln y = a + b ln x + μ \ln y = a + b\ln x + \mu lny=a+blnx+μ
x x x 每增加 1% ， y y y 平均变化 b% -
半对数模型： y = a + b ln x + μ y = a + b\ln x + \mu y=a+blnx+μ
x x x 每增加 1% ， y y y 平均变化 b 100 \frac{b}{100} 100b 个单位。 -
半对数模型： ln y = a + b x + μ \ln y = a + bx + \mu lny=a+bx+μ
x x x 每增加一个单位， y y y 平均变化 ( 100 b ) (100b) (100b)%
八、对于定性变量的处理——虚拟变量 X X X
在自变量中如果有定性的变量，例如：性别，地区等等，我们在回归的过程中可以将它们作为虚拟变量来处理
例如：我们要研究性别对于工资的影响
此时可以建立多元线性回归模型： y i = β 0 + δ 0 F e m a l e i + β 1 x 1 i + β 2 x 2 i + ⋯ + β k x k i + μ i y_i = \beta_0 + \delta_0Female_i + \beta_1x_{1i} + \beta_2x_{2i} + \cdots + \beta_kx_{ki} + \mu_i yi=β0+δ0Femalei+β1x1i+β2x2i+⋯+βkxki+μi F e m a l e i = 1 Female_i = 1 Femalei=1 表示第 i i i 个样本为女性； F e m a l e i = 0 Female_i = 0 Femalei=0 表示第 i i i 个样本为男性。
同时，这里面的核心解释变量即为： F e m a l e Female Female，控制变量为： x m ( m = 1 , 2 , ⋯ , k ) x_m(m = 1, 2, \cdots, k) xm(m=1,2,⋯,k)
九、下面来看一个实例
某电商平台846条奶粉的销售信息如下，每条信息由11个之变组成。其中评价量可以侧面反映顾客对产品的关注度。
完成下列问题：
- 以评价量为因变量，分析其他变量和评价量之间的关系；
- 以评价量为因变量，研究影响评价量的重要因素。
问题一：
- 在 S t a t a Stata Stata 中调用
tabulate 配方,gen(A)等将定性变量生成为虚拟变量。 - 对所有变量进行回归：
reg 评价量 团购价元 商品毛重kg A1-G4，得到的结果为：
正如图中所示，在前一部分的表格中我们首先需要关注的就是 P r o b > F Prob > F Prob>F 这一栏，判断我们所使用的模型是否有意义。
同时， R − s q u a r e d R-squared R−squared 和 A d j R − s q u a r e d Adj R-squared AdjR−squared 表示的是拟合优度以及调整后的拟合优度大小。
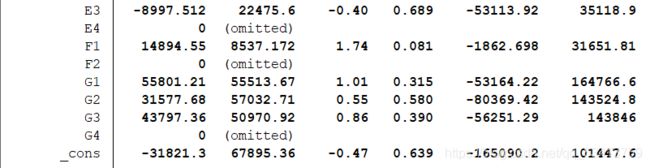
这张表表示的就是回归的结果。需要关注的有：第一列（Coef.）表示回归系数，第四列（P > |t|）表示 P 值大小。
在 95% 的置信水平下，P 值必须要小于 0.05 才有意义。
注意：由于完全多重共线性的影响，Stata会自动将一组变量中的某个变量作为参考变脸（表格中omitted的变量）。因此，一组变量如 F 组变量，在 90% 的置信水平下，我们可以解释为，在其他变量不变的情况下，F1 评价量平均要比 F2 高出14894.55。
问题二：
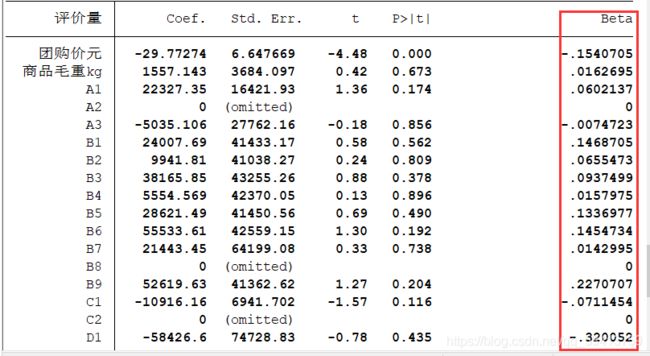
- 基本思路：利用标准化回归系数来解决。（去除量纲的影响）
标准化公式 y − y ˉ δ \frac{y - \bar{y}}{\delta} δy−yˉ， y ˉ \bar{y} yˉ 表示平均值， δ \delta δ 表示标准差。标准化系数的绝对值越大，说明对因变量的影响就越大（只关注显著的回归系数） - 在 S t a t a Stata Stata 中调用
reg 评价量 团购价元 商品毛重kg A1-G4,beta，然后关注最后一列，绝对值越大，代表影响越大。
十、扰动项需要满足的条件
扰动项需要满足“同方差”和“无自相关”两个条件。
十一、异方差
-
异方差的检验
- BP检验
在 S t a t a Stata Stata 中调用命令：estat hettest, rhs iid(回归结束之后)进行 BP 检验
原假设：扰动项不存在异方差
P 值小于 0.05，说明在 95% 的置信水平下拒绝原假设，即认为扰动项存在异方差。 - 怀特检验
在 S t a t a Stata Stata 中调用命令：eatat imtest, while(回归结束之后)
原假设：扰动项不存在异方差
同样，P 值小于 0.05，因此也要拒绝原假设。即扰动项也存在异方差。
- BP检验
-
异方差的处理
- 使用OLS(普通最小二乘估计法) + 稳健的标准误（推荐）
在 S t a t a Stata Stata 中调用命令：reg y x1...xk, robust
结果为：
可以看出显著的变量相比于之前多了许多 - 广义最小二乘法GLS
GLS得出的结果不稳健，也可能出现偶然性，因此不做介绍。
- 使用OLS(普通最小二乘估计法) + 稳健的标准误（推荐）
十二、多重共线性
-
多重共线性的检验
多重共线性的检验可以使用方差膨胀因子 V I F VIF VIF.假设有 k k k 个自变量，那么第 m m m 个自变量的 V I F m = 1 1 − R 1 − k / m VIF_m = \frac{1}{1 - R_{1-k/m}} VIFm=1−R1−k/m1
V I F m = 1 1 − R 1 − k / m VIF_m = \frac{1}{1 - R_{1-k/m}} VIFm=1−R1−k/m1 表示将第 m m m 个自变量作为因变量，对剩下的 k − 1 k - 1 k−1 个自变量回归得到的拟合优度。V I F VIF VIF 越大，说明第 m m m 个变量和其他变量的相关性越大。
定义 V I F = m a x { V I F 1 , V I F 2 , V I F 3 , ⋯ , V I F m } VIF = max\{VIF_1, VIF_2, VIF_3, \cdots, VIF_m\} VIF=max{VIF1,VIF2,VIF3,⋯,VIFm}，若 V I F > 10 VIF > 10 VIF>10，则认为模型具有严重的多重共线性。
在 S t a t a Stata Stata 中调用命令：
estat vif(回归之后)
2.多重共线性的解决
十三、逐步回归
-
向前逐步回归
将自变量逐个引入模型，每一个自变量加入后都要进行检验，显著时才加入回归模型。（缺点：引入变量后，原来显著的变量也可能变得不显著）在 S t a t a Stata Stata 中，调用命令：
stepwise regress y x1 x2...xk, pe(#1)，其中，#1表示显著水平（0.05） -
向后逐步回归
先将所有的自变量放入模型，之后再尝试将其中一个自变量从模型中删除，看整个模型解释因变量是否有显著变化，之后将最没有解释力的哪个自变量删除，知道没有自变量符合删除条件为止。在 S t a t a Stata Stata 中，调用命令：
stepwise regress y x1 x2...xk, pr(#2)，其中，#2也表示显著水平（0.05）
注意：
（1） x 1 , x 2 , x 3 , ⋯ , x k x1, x2, x3, \cdots, xk x1,x2,x3,⋯,xk 之间不能有完全多重共线性
（2）可以在后面加上参数 b 和 r ，即标准化回归系数和稳健标准误
（3）向前逐步回归和向后逐步回归的结果可能不同
（4）不要轻易使用逐步回归，删除了变量会导致其他问题
十四、总结
使用多元线性回归时，可以参考以下步骤：
- 确定自变量和因变量
- 对定性的变量生成虚拟变量
- 异方差检验以及多重共线性检验并分别进行处理
- 在 S t a t a Stata Stata 中进行回归分析，多元线性回归？标准化回归？逐步回归？……
- 得出结论
本文是看了课视频和PPT之后自己的总结，有什么错误还望指出，thx！！
