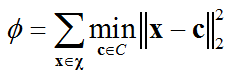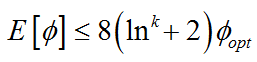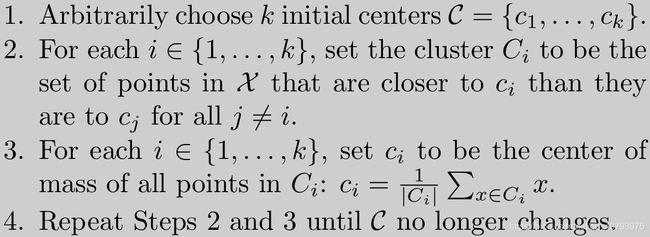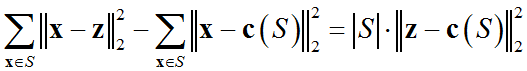K-Means++详解

k-means++ The Advantages of Careful Seeding

第三十一次写博客，本人数学基础不是太好，如果有幸能得到读者指正，感激不尽，希望能借此机会向大家学习。由于K-Means++是标准K-Means的一种优化算法，因此这篇文章作为原型聚类中介绍的第六篇，其他有关于原型聚类算法的讨论可以移步到该类算法的导航页《原型聚类算法综述（原型聚类算法开篇）》。

传统K-Means聚类方法的缺点？

  在K-Means聚类问题中，给定聚类数量$k$和数据集$\chi \in {\mathbb{R}}^{n\times d}$，聚类目标是要最小化目标函数$\varphi$，该函数计算数据集中所有样本点与其最近的质心之间距离（2-范数）的平方和（见式（1）），在这篇文章中，该函数也被做为用来表征聚类性能的“势函数”（Potential Function）。假设，$k$个簇质心的集合$C=\{{\mathbf{c}}_1,{\mathbf{c}}_2,...,{\mathbf{c}}_k\}$，那么势函数可以表示为，

  传统K-Means聚类方法选择初始簇质心的方法是，在数据集$\chi$进行均匀随机采样，这种算法虽然相较于其他解决上述NP-hard问题的算法，在时间复杂度和精度上都有较好的保证，但是实验证明该算法的速度和时间复杂度的改善是以聚类精度为代价的。另外，假设K-Means问题的最优聚类集合是$C_{opt}$​，${\varphi }_{opt}$是$C_{opt}$​对应的最优势函数，传统K-Means聚类产生的聚类集合是$C$，$\varphi$是$C$对应的最优势函数，由于$\frac{\varphi }{{\varphi }_{opt}}$​的上界并不依赖于参数$n$和$k$的取值，因此在很多情况下该算法会得到较差的聚类效果。

之前的关于改善传统K-Means聚类的研究？

  尽管传统K-Means算法有精度上的限制，但是由于他使用方便而且具有客观的收敛速度，至今仍被广泛应用，很多相关学者均提出了各种提升该算法收敛速度的方法，这里主要讨论提升算法精度的相关研究成果。
  在理论界，Lnaba等人首先提出了时间复杂度为$O\left(n^{kd}\right)$、具有精确聚类结果的改进算法。至此，许多近似的研究成果不断涌现，研究人员开始致力于观察聚类问题的内部结构，但是这类改进算法的时间复杂度大多是$k$的指数级甚至更糟。随后，Kanungo等人提出了一种时间复杂度为$O\left(n^3{\epsilon }^{-d}\right)$、近似聚类精度为$O\left(9+\epsilon \right)$（这里“近似聚类精度”是指$\frac{\varphi }{{\varphi }_{opt}}$）的改进算法，但是注意到该算法的时间复杂度与原始数据集所在的空间维度$d$有关，只有丢弃算法中的所有近似性担保时，才能忽略$d$对时间复杂度的影响，但是这也会大大降低算法的聚类精度。由Mattu和Plaxton等人提出的改进算法虽然具有$O\left(1\right)$的近似聚类精度，$O\left(nkd\right)$的时间复杂度，但是这种算法只有在kk足够大，且每个簇的规模足够小时，才能达到上述的聚类效果。后来，由Ostrovsky等人提出的K-Means++算法（和本文分析的算法同名）同样具有$O\left(1\right)$的近似聚类精度和$O\left(nkd\right)$的时间复杂度，但是只需要满足$\frac{{\varphi }_{opt,k}}{{\varphi }_{opt,k-1}}\le {\epsilon }^2$，对该不等式的直观理解是“如果不满足该不等条件，那么$k$的取值不合适”，需要注意的是，为了达到上述效果需要在明显分离的数据集上运行该算法。

本文提出的改进算法？

  本文提出了一种新的随机选择初始质心的方法，具体的说，我们以某一个概率将样本点$P$作为初始质心，该概率与$P$对聚类的整体势（即$\varphi$，或称“整体性能”）的贡献成正比，使用该方法与K-Means算法结合得到的新算法称为K-Means++，与Ostrovsky等人提出的K-Means++算法本质上是相同的，但是分析过程完全不同。本文在分析过程中引出如下定理，
  定理 对于任意的数据集，如果簇集合$C$是通过K-Means++算法得到的，那么聚类的整体势函数$\varphi$满足下述不等式

并由此得到如下结论，
  对于任意数据集，K-Means++算法的时间复杂度是$O\left(nkd\right)$，近似聚类精度是$O\left(\log k\right)$，此外，由于定理与某个常数因素有关，因此可以将该定理对于任意度量空间中的不同势函数仍然成立，因此，使用这种随机初始化簇质心的方法可以得到近似聚类精度为$O\left(\log k\right)$的K-Median算法，该算法采用1-范数计算势函数。

算法步骤？

  首先回顾一下K-Means聚类问题，给定聚类数量kk和数据集$\chi \in {\mathbb{R}}^{n\times d}$，聚类目标是要最小化目标函数$\varphi$，该函数计算数据集中所有样本点与其最近的质心之间距离（2-范数）的平方和（见式（1））。传统K-Means聚类的伪代码如下所示，这里就不做多余的阐述了，

图1 传统K-Means聚类

上述伪代码中的第2、3步都致力于降低聚类的整体势，给出引理
  引理 令$S$表示某个样本点集合，$\mathbf{c}\left(S\right)$是该样本点集合的质心，$\mathbf{z}$是一个任意点，那么由如下不等式成立

借助上述引理可以得知第3步通过将$S$作为一个单独的簇，并且令$\mathbf{z}$作为该簇的质心，来保证每次执行这一步时，整体势$\varphi$是单调递减的。
  下面给出K-Means++算法伪代码，其中$D\left(\mathbf{x}\right)$表示在任意时刻样本点$\mathbf{x}$与其最近质心之间的距离，

图2 K-Means++聚类

由上图可知，在选择聚类初始质心时（1a），K-Means++首先从数据集$\chi$中均匀随机选择一个样本点作为第一个初始质心${\mathbf{c}}_1$​，在选择其余初始质心${\mathbf{c}}_i={\mathbf{x}}^{\prime }\in \chi$时（1b），首先对数据集中其余的样本点计算概率$\frac{D{\left({\mathbf{x}}^{\prime }\right)}^2}{{\sum }_{\mathbf{x}\in \chi }D{\left(\mathbf{x}\right)}^2}$，然后选择概率最大的样本点作为下一个初始质心，这一步也称为“$D^2$权值化”（$D^2$ weighting），重复1b直到产生$k$个初始质心为止（1c），其余步骤（2-4）与传统K-Means聚类中对应步骤一致。

参考资料

【1】 Arthur, D , et al. “k-means++: The advantages of careful seeding.” Eighteenth Acm-siam Symposium on Discrete Algorithms Society for Industrial and Applied Mathematics, 2007.

---

代码实现及对比

下面是我自己实现的K-Means++代码，通过之前的介绍可知，K-Means++实际上是一种选择初始质心的算法，在得到初始质心后，其他处理过程与标准K-Means相同，为了便于对比，代码中还加入了其他选择初始质心的方法，大家有兴趣的话可以进行对比。在文章后面对K-Means++与标准K-Means的运行结果进行了对比。

代码细节

"""

@author: Ἥλιος
@CSDN：https://blog.csdn.net/qq_40793975/article/details/84385970

"""
print(__doc__)

import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import KMeans
import random
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice


# 加载数据集（从文件中）
def load_Data1(filename):
    data_set = []
    with open(filename) as fi:
        for line in fi.readlines():
            cur_line = line.strip().split('\t')
            flt_line = []
            for i in cur_line:
                flt_line.append(float(i))
            data_set.append(flt_line)
    data_mat = np.mat(data_set)  # 转化为矩阵形式
    return data_mat


# 加载数据集（自建数据集）
def load_Data2(n_samples=1500):
    # 带噪声的圆形数据
    noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05)

    # 带噪声的月牙形数据
    noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)

    # 随机分布数据
    no_structure = np.random.rand(n_samples, 2), np.ones((1, n_samples), dtype=np.int32).tolist()[0]

    # 各向异性分布数据（Anisotropicly distributed data）
    random_state = 170
    X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
    transformation = [[0.6, -0.6], [-0.4, 0.8]]
    X_aniso = np.dot(X, transformation)
    aniso = (X_aniso, y)

    # 不同方差的气泡形数据（blobs with varied variances）
    varied = datasets.make_blobs(n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state)

    # 相同方差的气泡形数据
    blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)

    # 合并数据集
    data_sets = [noisy_circles, noisy_moons, no_structure, aniso, varied, blobs]
    cluster_nums = [2, 2, 3, 3, 3, 3]
    data_mats = []
    for i in range(data_sets.__len__()):
        X, y = data_sets[i]
        X = StandardScaler().fit_transform(X)  # 对数据集进行标准化处理
        X_mat = np.mat(X)
        y_mat = np.mat(y)
        data_mats.append((X_mat, y_mat))

    # 展示数据集
    plt.figure(figsize=(2.5, 14))
    plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05, hspace=.01)
    for i in range(data_sets.__len__()):
        X, y = data_sets[i]
        X = StandardScaler().fit_transform(X)  # 对数据集进行标准化处理
        colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a', '#f781bf', '#a65628', '#984ea3', '#999999',
                                             '#e41a1c', '#dede00']), int(max(y) + 1))))
        plt.subplot(len(data_sets), 1, i+1)
        if i == 0:
            plt.title("Self-built Data Set", size=18)
        plt.scatter(X[:, 0], X[:, 1], c=colors[y], s=10)
        plt.xlim(-2.5, 2.5)
        plt.ylim(-2.5, 2.5)

    plt.show()

    return data_mats, cluster_nums


# 计算样本点A与B间距离（欧氏距离）
def dist_Euclid(VecA, VecB):
    return np.sqrt(np.sum(np.power(VecA-VecB, 2)))


# 这个数据集的距离矩阵
def dist_Matrix(data_mat):
    m = np.shape(data_mat)[0]
    distMatrix = np.mat(np.zeros((m, m)))
    for i in range(m):
        for j in range(i+1, m):
            distMatrix[i, j] = distMatrix[j, i] = dist_Euclid(data_mat[i, :], data_mat[j, :])
    return distMatrix


# 带权随机采样
def weighted_RandomSample(data, weight):
    probabilities = (np.array(weight) / sum(weight)).tolist()
    prob = random.random()
    probSum = 0.0
    for i in range(len(probabilities)):
        probSum += probabilities[i]
        if prob < probSum:
            return data[i]
    print("Error in Weighted Sampling!")
    return -1


# 对k个聚类中心随机初始化(随机选取数据集中的k个样本点）
def rand_initial_center1(data_mat, k):
    (m, n) = np.shape(data_mat)
    centroids = np.mat(np.zeros((k, n), dtype=np.float32))
    for i in range(k):
        index = int(np.random.rand()*m)
        centroids[i, :] = data_mat[index, :]
    return centroids


# 对k个聚类中心随机初始化（在样本空间范围内随机选取）
def rand_initial_center2(data_mat, k):
    n = np.shape(data_mat)[1]
    centroids = np.mat(np.zeros((k, n), dtype=np.float32))
    for i in range(n):
        minJ = np.min(data_mat[:, i])
        maxJ = np.max(data_mat[:, i])
        centroids[:, i] = np.mat(np.random.rand(k, 1)*(maxJ - minJ)) + minJ
    return centroids


# 对k个聚类中心随机初始化（K-Means++）
def rand_initial_center3(data_mat, k):
    m, n = np.shape(data_mat)
    centroidsIndexList = []   # 质心对应的索引
    distMatrix = dist_Matrix(data_mat)  # 计算距离矩阵
    alldataIndex = np.array([j for j in range(m)])  # 保存所有样本的索引
    for i in range(m):
        distMatrix[i, i] = np.inf   # 由于后面需要计算最小距离，因此这里将距离矩阵对角线上的值置正无穷
    print("------------------初始质心质心的选取过程----------------")
    initialCenterIndex = int(random.random() * m)   # 选择初始质心
    print("初始质心的索引：", initialCenterIndex)
    # initialCenterIndex = 79
    centroidsIndexList.append(initialCenterIndex)
    for i in range(k - 1):
        print("------------------第", i+2, "个质心的选取过程-----------------")
        restDistMatrix = distMatrix[:, centroidsIndexList]   # 这里只关注每个样本点与现有质心之间的距离
        minDistArray = np.argmin(restDistMatrix, axis=1).T.A[0]     # 每个样本点对应的最小距离的质心索引
                                                                    # （注意该索引与alldataIndex中的数据原始索引不同）
        weightArray = np.min(restDistMatrix, axis=1).T.A[0]     # 每个样本点与最近质心之间的距离

        # 剔除距离为np.inf对带权随机采样的影响（原因在后面有解释）
        NonInfIndexList = np.nonzero(weightArray != np.inf)[0].tolist()  # 这里关注那些距离不为正无穷的样本
        NonInfminDistArray = minDistArray[NonInfIndexList]
        NonInfweightArray = weightArray[NonInfIndexList]
        NonInfdataIndex = alldataIndex[NonInfIndexList]

        # # 加入随机性（使用带权随机采样，权值依赖于样本点与其最近质心之间的距离）
        # sampleIndex = weighted_RandomSample([i for i in range(len(NonInfdataIndex))], NonInfweightArray)
        # 不加入随机性（直接在全部距离中选择最大距离，“全部距离”是指各个样本点与其最近质心之间的距离组成的集合）
        sampleIndex = np.argmax(NonInfweightArray)
        print("实际的最大距离：", np.max(NonInfweightArray))
        print("经带权随机采样得到的最大距离：", NonInfweightArray[sampleIndex])

        nextCenterIndex = NonInfdataIndex[sampleIndex]  # 下一个质心的索引
        centroidsIndexList.append(nextCenterIndex)
        bound2nextCenterIndex = centroidsIndexList[NonInfminDistArray[sampleIndex]]   # 与该质心距离最近的已有质心索引
                                                                                      # （这里采用原始数据索引）
        print("该轮迭代选取的质心：", nextCenterIndex)
        print("与该轮迭代选取的质心距离最近的质心索引：", bound2nextCenterIndex)

        for centroid in centroidsIndexList:
            distMatrix[nextCenterIndex, centroid] = distMatrix[centroid, nextCenterIndex] = np.inf
    centroids = data_mat[centroidsIndexList, :]
    print("全部质心的索引", centroidsIndexList)
    return centroids


# data_mat = load_Data1("C:\\Users\\Administrator\\Desktop\\testSet.txt")
# centroids = rand_initial_center3(data_mat, 4)
# print("------------------------------------------------------")
# print("全部质心：", centroids)
# fig = plt.figure()
# plt.scatter(data_mat[:, 0].T.A[0], data_mat[:, 1].T.A[0], c='b', s=10)
# plt.scatter(centroids[:, 0].T.A[0], centroids[:, 1].T.A[0], c='r', s=20)
# fig.show()


# 标准K-均值
# 输入：
#       data_mat：数据集
#       k：簇个数
#       dist_measure：距离衡量方法
#       centroid_select_method：初始质心选择方法
# 输出：
#       centroids：聚类质心集合
#       cluster_assment：各样本的预测标记集合
#       t0：算法运行的开始时间
#       t1：算法运行的开始时间
def standard_KMeans(data_mat, k, dist_measure=dist_Euclid, centroid_select_method=rand_initial_center1):
    (m, n) = np.shape(data_mat)
    centroids = centroid_select_method(data_mat, k)  # 初始化质心
    t0 = time.time()  # 计算运行时间
    cluster_assment = np.mat(np.zeros((m, 2)), dtype=np.float32)  # 存储每个样本点的簇隶属和距该簇的质心距离
    cluster_changed = True  # 簇质心发生改变
    while cluster_changed:
        cluster_changed = False
        for i in range(m):  # M步：更新样本点的簇信息
            min_dist_ji = np.inf  # 样本点与当前所有质心之间的最短距离
            min_dist_index = -1  # 距离当前样本点最近的质心的簇标号
            for j in range(k):
                dist_ji = dist_measure(centroids[j, :], data_mat[i, :])  # 计算当前样本点与所有簇质心之间的距离
                if dist_ji < min_dist_ji:   # 如果该距离小于当前的最小距离
                    min_dist_ji = dist_ji
                    min_dist_index = j
            if cluster_assment[i, 0] != min_dist_index:  # 如果样本点的簇隶属发生改变就继续迭代
                cluster_changed = True
            cluster_assment[i, 0] = min_dist_index
            cluster_assment[i, 1] = min_dist_ji
        for i in range(k):   # E步：更新各个簇质心
            pts_in_cluste = data_mat[np.nonzero(cluster_assment[:, 0].A == i)[0], :]  # 提取隶属于当前簇的所有样本点
            if np.shape(pts_in_cluste)[0] != 0:
                centroids[i, :] = np.mean(pts_in_cluste, axis=0)

    t1 = time.time()

        # # 动态显示(！不要再Pycharm中运行，会变成幻灯片）
        # plt.scatter(data_mat[:, 0].T.A[0], data_mat[:, 1].T.A[0], c=cluster_assment[:, 0].T.A[0])
        # plt.scatter(centroids[:, 0].T.tolist()[0], centroids[:, 1].T.tolist()[0], s=100, c='red', marker='x')
        # plt.show()
        # plt.pause(1)
        # plt.clf()

    return centroids, cluster_assment, t0, t1


# standard K-Means
data_mats, cluster_nums = load_Data2()
plt.figure(figsize=(2.5, 14))
plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05, hspace=.01)
for i in range(len(data_mats)):
    data_mat = data_mats[i][0]  # 获取自建数据集
    k = cluster_nums[i]  # 获取自建数据集的簇标记
    centroids, cluster_assment, t0, t1 = standard_KMeans(data_mat, k, centroid_select_method=rand_initial_center3)  # 自己实现的
    # y_pred = KMeans(n_clusters=k, random_state=170).fit_predict(data_mat)  # sklearn的实现

    y_pred = np.array(cluster_assment[:, 0].T, dtype=np.int32)[0]  # 预测的簇标记，用于画图（使用sklearn的K_Means时可以注释掉）
    colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a', '#f781bf', '#a65628', '#984ea3', '#999999',
                                         '#e41a1c', '#dede00']), int(max(y_pred) + 1))))
    plt.subplot(len(data_mats), 1, i + 1)
    if i == 0:
        plt.title("Self-programming Implementation", size=10)
        # plt.title("Sklearn Implementation", size=15)
    plt.scatter(data_mat[:, 0].T.A[0], data_mat[:, 1].T.A[0], c=colors[y_pred], s=10)
    plt.xlim(-2.5, 2.5)
    plt.ylim(-2.5, 2.5)
    plt.text(.99, .01, ('%.2fs' % (t1 - t0)).lstrip('0'), transform=plt.gca().transAxes, size=15,
             horizontalalignment='right')
plt.show()

代码解释

1.带权随机初始化

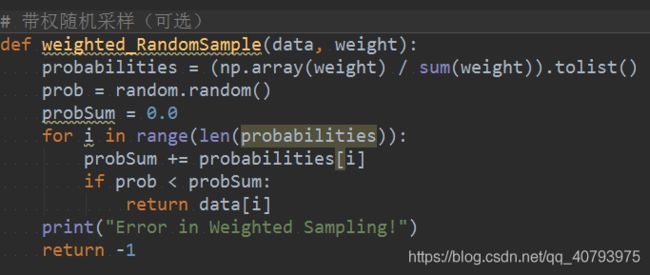
  这部分代码主要是对样本点进行随机采样，给定样本集与每个样本的权重，该函数会采样得到一个样本点作为输出，这里每个样本的“权重”即上文提到过的$\frac{D{\left({\mathbf{x}}^{\prime }\right)}^2}{{\sum }_{\mathbf{x}\in \chi }D{\left(\mathbf{x}\right)}^2}$，这个函数是可选的，也可以直接将权重最大的样本作为输出，如下图所示，

在命令行输出中，可以清晰的分辨出这两者之间的差别，如下图所示，是不加入随机性的输出结果，可以看出“实际最大距离”与“经带权随机采样得到的最大距离”是相同的，在加入随机性后，这两者可能不同，

关于带权随机初始化还有一点要解释的，在第一次迭代，即选取第二个初始质心时，我们所关注的矩阵restDistMatrix中必定存在一个np.inf值，这是在初始化距离矩阵时加入到矩阵对角线中的，这时将np.inf对应的概率必定为1，这会使得带权随机初始化无效，并且得到错误输出，因此需要对这些值进行剔除，如下图所示

2.K-Means++过程的可视化
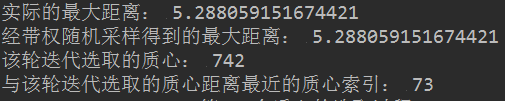
  为了使得K-Means++中选取质心的过程透明化，在命令行中将每个初始质心的挑选过程可视化了出来，如下图所示，

“该轮迭代选取的质心：742”代表本次迭代选出的初始质心是原始数据集中的第742个样本点，“与该轮迭代选取的质心距离最近的质心索引： 73”是指与742距离最近的质心（已经存在于初始质心列表中的）是原始数据集中的第73个样本点。

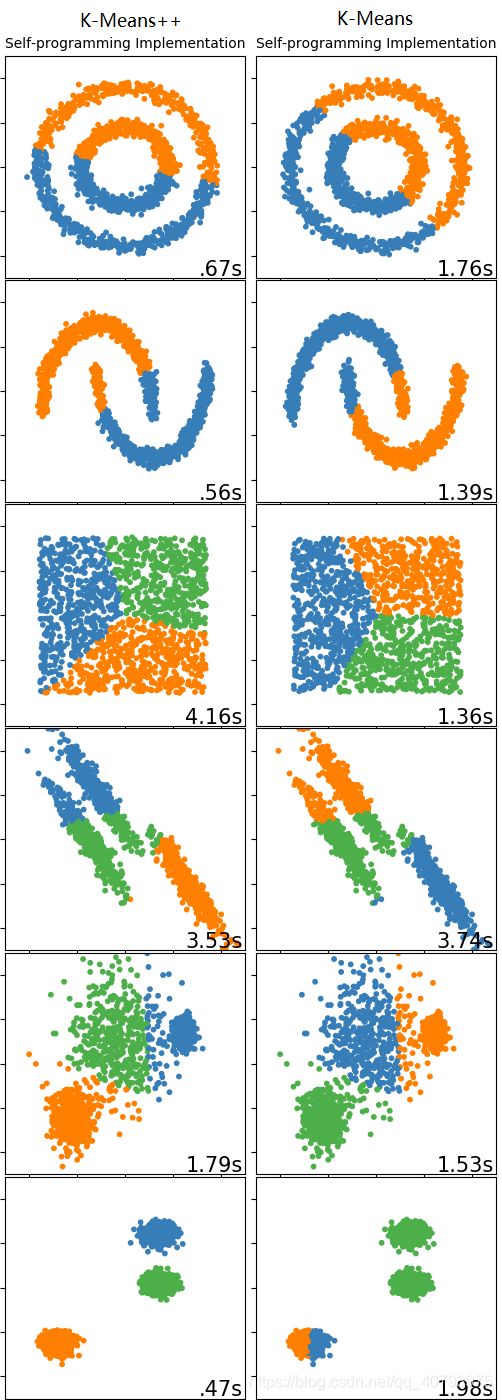
算法对比

  如上图所示是标准K-Means与K-Means++的实际效果差别，可以看出K-Means++的运行时间几乎总是低于标准K-Means，这与之前的讨论是相符合的，另外值得注意的一点是，对于最后一个数据集，K-Means++能够对其正确聚类，但是传统K-Means得到了错误的聚类结果，这也说明了这种初始化质心的方法有助于提高聚类质量。