BP神经网络详解+原理

 

本文将会从实际的训练过程来依次讲解，用到哪些知识点就将～

BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。（来源：百度百科）

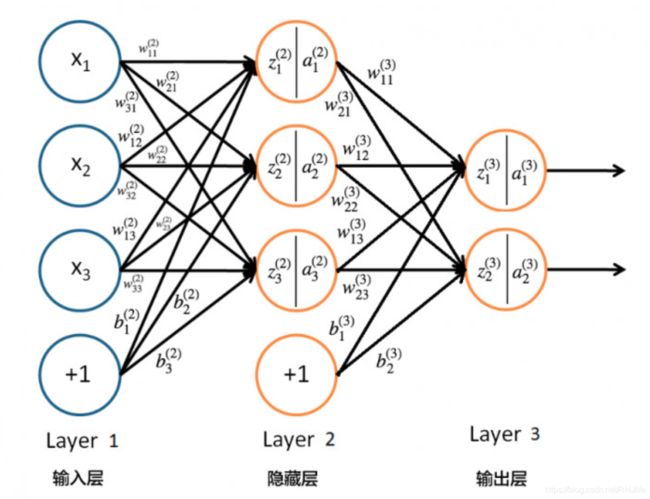
先来一个神经网络结构图：

 

首先解释下：输入层、隐藏层、输出层。

输入层其实就是输入的训练数据，他的格式也由输入数据决定，可能10*1，可能2*2；而隐藏层其实就是指神经网络的参数（也叫权重矩阵），他不一定是1层（本图以1层为例），这里说一下几个常用概念，神经元个数->其实就是值某层里的结点数，（隐藏层）层数->其实就是隐藏层有多少层，往往神经网络设计的时候重点考虑的就是：设计几层？每层多少个神经元？（有的层数是指输入+隐藏+输出，本文里暂时认为是单指隐藏层了）

这里解释一个问题：为什么神经网络这样设计？？

这个问题我刚入门的时候就经常会这么问，现在我的理解是 根据训练的数据，有经验的人可以大概感觉用几层、每层多少神经元，然后进行初步设计，在训练过程中不断的调整层数和神经元个数，最终找到一个效果满意的层数和神经元个数；又或者是一些前辈们总结的经验，往往采用一个大部分情况都比较合适层数和神经元个数作为初步设计，然后不断调整。说白了就是，我们并不知道到底多少层，每层有多少神经元才是最优的，而效果良好的模型往往都是不断调整/优化出来的。

再往后说，当我们设计了一个神经元模型后，数据到底是怎么训练的呐？

（以下关于正向传播以及反向传播推到以及数学相关内容均来自于博客大佬痴澳超博客内容，以下是原文链接https://blog.csdn.net/u014303046/article/details/78200010/，已获得作者关于转载内容的同意～）

首先输入的数据会与权重矩阵做矩阵乘法

这个地方我稍作解释一下，简单理解就是输入的数据和第一层的神经元相连接，其实就是矩阵乘法，如下：

如果看不懂其他的公式也没关系，关键是这一部分，其实就是权重矩阵（W）乘输入层矩阵（A）最后加一个偏置矩阵（B），这里可能大家会有疑惑。输入层矩阵是输入的数据我知道，但是权重矩阵和偏置矩阵我并不知道是多少啊？？

这个问题我就说一下啦～其实一开始的权重矩阵和偏置矩阵矩阵其实都是人为设置的初始值，也就是第一次的结果肯定是不准确的，这就是前向传播。

这里我在解释一下关于BP网络的概念，毕竟一开始百度百科的话，对于很多人不太友好，BP神经网络是一种多层的前馈神经网络，其主要的特点是：信号是前向传播的，而误差是反向传播的。举个很多教程或者博客都有的例子就是，我要追求女神，那我总得表示一下吧！于是我给她买花，讨她欢心。然后，她给我一些表示（或者叫暗示），根据这个表示，与我最终目的进行对比（追求到女神），然后我进行调整继续表示，改成吃饭或者送其他礼物，一直循环往复（她继续暗示，我继续调整表示），知道实现最终目的——成功最求到女神。我的表示 就是“信号前向传播”，女神的表示 就是“误差反向传播”。这就是BP神经网络的核心。

而且前向传播其实就是刚刚说的，从输入层传递到隐藏层（如果隐藏层有多层其实也是上一层隐藏层传递到下一层隐藏层），这个传递其实：权重矩阵（W）乘输入层矩阵（A）最后加一个偏置矩阵（B）

这里还有一个激活函数的概念，这里可以参考我写的文章https://blog.csdn.net/RHJlife/article/details/104743421中激励层的相关概念～

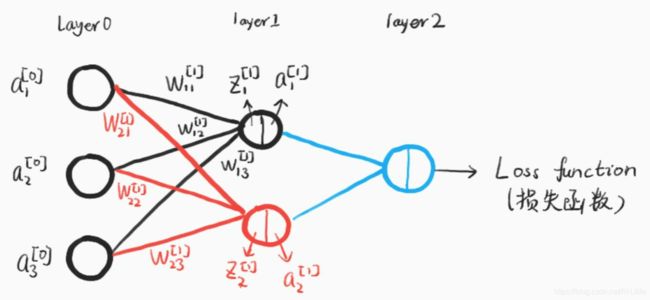
刚刚说了如果给女神送礼物，那么现在说说女神如何暗示了～，这里主要牵扯两个概念损失函数和反向传播，这里我简单解释下损失函数了。

损失函数其实就是用来表示预测值（模型算出来的结果）与已知答案（实际正确的答案）的差距。在训练神经网络是，通过不断改变神经网络中所有参数，使损失函数不断减小，从而训练出更高的准确率的神经网络模型。常用的损失函数有均方误差、自定义和交叉熵等。

损失函数可以理解成女神的暗示～就是女神告诉你，你送的礼物和我想要的不太一样啊～

然后我们如何调整送的礼物哪？这就牵扯到 女神给我们暗示了，我们要读的懂这个暗示然后来调整我们的表示。

反向传播的基本思想就是通过计算输出层与期望值之间的误差来调整网络参数，从而使得误差变小。（就是刚刚说的，误差大概是女神的暗示，通过误差调整网络使误差变小就是通过女神的暗示，使我们的表示与女神真实想要的表示越来越近）

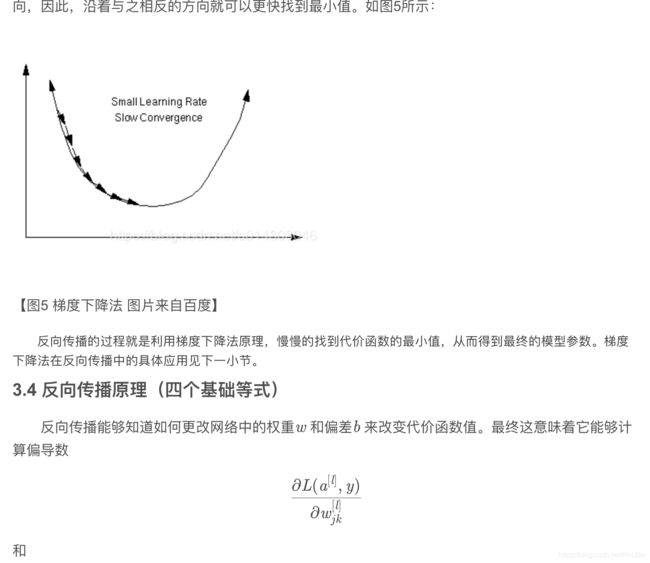
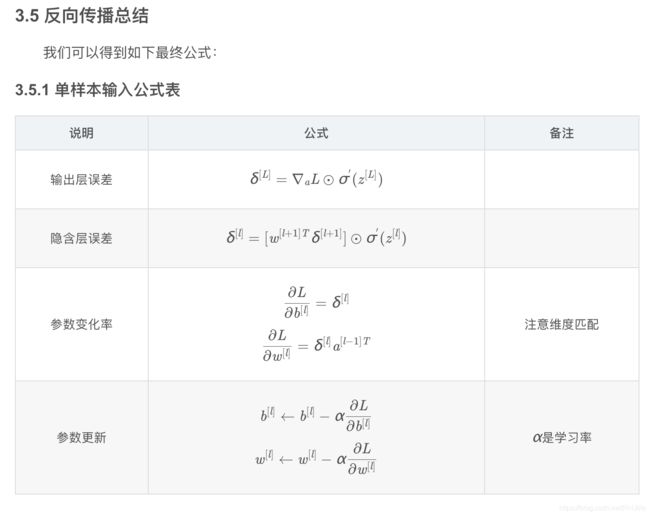
首先来一段原理轰炸（博客大佬痴澳超博客内容）～

3.5.3 关于超参数

  通过前面的介绍，相信读者可以发现BP神经网络模型有一些参数是需要设计者给出的，也有一些参数是模型自己求解的。

  那么，哪些参数是需要模型设计者确定的呢？

  比如，学习率α，隐含层的层数，每个隐含层的神经元个数，激活函数的选取，损失函数（代价函数）的选取等等，这些参数被称之为超参数。

  其它的参数，比如权重矩阵w和偏置系数b在确定了超参数之后是可以通过模型的计算来得到的，这些参数称之为普通参数，简称参数。

  超参数的确定其实是很困难的。因为你很难知道什么样的超参数会让模型表现得更好。比如，学习率太小可能造成模型收敛速度过慢，学习率太大又可能造成模型不收敛；再比如，损失函数的设计，如果损失函数设计不好的话，可能会造成模型无法收敛；再比如，层数过多的时候，如何设计网络结构以避免梯度消失和梯度爆炸……

  神经网络的程序比一般程序的调试难度大得多，因为它并不会显式报错，它只是无法得到你期望的结果，作为新手也很难确定到底哪里出了问题（对于自己设计的网络，这种现象尤甚，我目前也基本是新手，所以这些问题也在困扰着我）。当然，使用别人训练好的模型来微调看起来是一个捷径……

  总之，神经网络至少在目前来看感觉还是黑箱的成分居多，希望通过大家的努力慢慢探索吧。
以上就是转载大佬的内容了，是不是头很晕...不管你们咋样，反正我是有点懵逼...这里我就简单说一下我关于反向传播的简单理解吧，其实就是根据损失函数的结果（误差值），用一种梯度下降的方法来调整权重矩阵（说实话 梯度下降比较难理解，如果想具体了解如何实现和如何推导等请详细看上面转载的内容，如果感觉目前没法理解...就简单的记住：根据损失函数的结果，用一种梯度下降的方法来调整权重矩阵，具体怎么实现的为什么能调整就暂时可以不用管，光知道梯度下降可以根据误差值 去调整权重矩阵使误差值会越来越小）

最后大家肯定还有一个疑问，比如模型是如何判断是这个结果的？唉？这个问题好像也有点抽象，那就举个例子，比如识别动物，如何确定这个图片是猫、狗、鱼哪？可以用0、1、2来分别代替。其实很多时候神经网络输出的并不是一个离散的，可能是个概率，例如判定是不是车，可能给你的是个概率值，不过根据一些博客看貌似是用最大似然估计来弄的，这一块我也不是很清楚，有了解的可以评论告知下～