U-Net听课笔记
目录
- 前言
- 1. 模型的特点
- 2. 模型结构
- 3. 思考与分析
-
- 3.1 边缘数据缺失
- 3.2 损失函数和权重划分
- 参考
前言
U-Net是一篇2015年针对生物医学影像分割提出的论文,采用Encoder-Decoder的结构,是当时较早采用全卷积网络进行语义分割的算法之一。
1. 模型的特点
U-Net网络的创新之处:
- 权重划分。在细胞与细胞之间的区域,施加一个更大的权重。而在大片的背景区域,则施加一个比较小的权重。
- 采用数据增强的方法,使得模型能够在训练样本较少的条件下也能训练。
- 采用多尺度特征,兼顾局部特征和全局语义。
U-Net网络的不足:
- 由于卷积时padding=0,导致每次卷积后特征层大小都会变换,在进行特征融合时需要裁边操作,增加了模型设计的难度。
- 采用转置卷积进行上采样,在效果上与双线性插值上采样相近,但是参数量会大大增加。
2. 模型结构
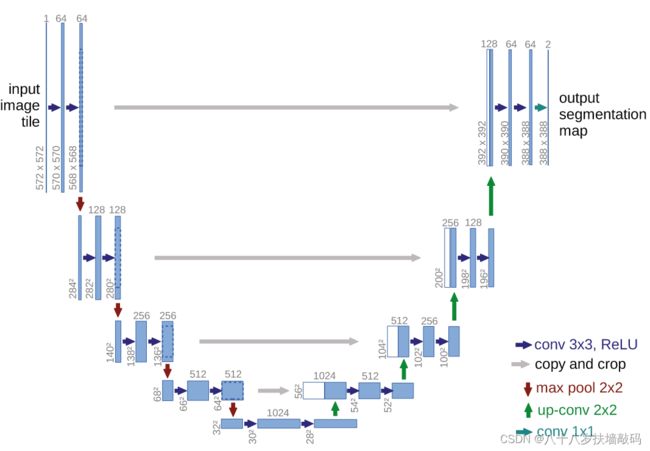
Encoder对应U形左边的部分(contracting path),用于特征提取和下采样。Decoder对应右边的部分(expansive path),通过一系列上采样得到最终的分割图。结构图中每一个长条的矩形都是一个特征层,不同颜色的箭头代表不同处理操作。(当时Batch Normalization还没火起来,没有使用到BN模块)
输入以 572 × 572 572 \times 572 572×572的单通道图像为例,首先会通过一个步距为1、填充为0、大小 3 × 3 3 \times 3 3×3、通道数为64的卷积层,ReLU激活,输出大小 570 × 570 570 \times 570 570×570。然后再通过一个卷积层,输出 568 × 568 × 64 568 \times 568 \times 64 568×568×64的特征图。
通过一个 2 × 2 2 \times 2 2×2的最大池化下采样,高宽减半,得到 284 × 284 × 64 284 \times 284 \times 64 284×284×64的特征图。再通过两个通道数为128的卷积层,得到输出 280 × 280 × 128 280 \times 280 \times 128 280×280×128的特征图。
以此类推,再次经过3次下采样后,得到 32 × 32 × 512 32 \times 32 \times 512 32×32×512大小的特征图,再通过两个 3 × 3 3 \times 3 3×3的卷积层,得到 28 × 28 × 1024 28 \times 28 \times 1024 28×28×1024的特征图。
接下来,使用转置卷积进行上采样,高和宽放大两倍,通道数减半(对应蓝色部分),输出 56 × 56 × 512 56 \times 56 \times 512 56×56×512的特征图。将之前 64 × 64 × 512 64 \times 64 \times 512 64×64×512大小的特征图进行中心裁剪,与蓝色部分进行拼接,通道数变为1024。再通过两个卷积层,将通道数调整为512
再经过3次相同操作,最终得到 388 × 388 × 64 388 \times 388 \times 64 388×388×64大小的特征层。
最后,经过 1 × 1 1 \times 1 1×1卷积层,得到 388 × 388 × 2 388 \times 388 \times 2 388×388×2的输出分割图。(分类个数为2)
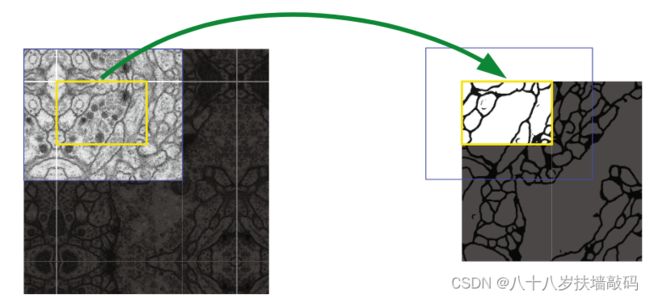
以下图为例,如果按照原论文中的实现方法,输入图像大小是蓝色框对应区域,那么所得到的分割图像只有黄色框内的区域。
目前的实现方法中,卷积层通常会加上padding,保证不会改变特征层高和宽的大小,这样在拼接时就不需要中心裁剪。并且,在卷积核ReLU中间会加上BN模块。如下图所示:

3. 思考与分析
3.1 边缘数据缺失
针对一个高分辨率的图片进行分割,如果直接将整张图片进行分割,很可能会爆显存。常见的方法是每次只去分割一个Patch,相邻的两个Patch之间一般会有一个重叠的部分,也就是overlap。这样就能更好地分割边界区域的信息。
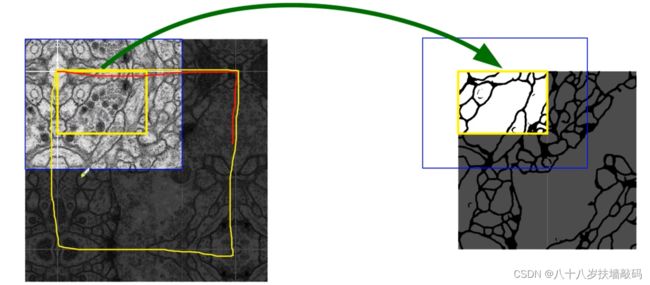
回到原论文中,假设要预测的区域是笔画出来的黄色的区域,在左上角的边缘部分的预测,则需要蓝色框内的图片信息才能得到。但是边缘之外的像素是没有输入到模型中的,也就是Missing input data。为了应对这个问题,对于缺失的数据U-Net直接采用了镜像的策略,分割图像边缘的信息。
而如果加上padding,保持特征图高宽不变的话,则不需要考虑边缘缺失数据的问题。
3.2 损失函数和权重划分
U-Net使用的是带有边界权重的损失函数:
E = ∑ x ∈ Ω w ( x ) l o g ( p l ( x ) ( x ) ) E = \sum_{x \in \Omega}w(x)log(p_{l(x)}(x)) E=x∈Ω∑w(x)log(pl(x)(x))
其中, l : Ω → { 1 , … , K } l : \Omega \rightarrow \lbrace1,\ldots,K\rbrace l:Ω→{1,…,K}是每个像素点的真实标签, K K K代表类别个数。 w : Ω ∈ R w: \Omega \in \mathbb R w:Ω∈R是像素点的权重,可以给图像中贴近边界点的像素更高的权重,其计算如下:
w ( x ) = w c ( x ) + w 0 ⋅ e x p ( − ( d 1 ( x ) + d 2 ( x ) ) 2 2 σ 2 ) w(x) = w_c(x) + w_0 \cdot exp(- \frac{(d_1(x) + d_2(x))^2}{2 \sigma ^2}) w(x)=wc(x)+w0⋅exp(−2σ2(d1(x)+d2(x))2)
其中, w c w_c wc是平衡类别比例的权重,d_1代表到最近的细胞边界的距离,d_2代表到第二近的细胞边界的距离。 w 0 w_0 w0和 σ \sigma σ是常数值,基于经验设定 w 0 = 10 w_0 = 10 w0=10, σ ≈ 5 \sigma \approx 5 σ≈5像素。
下图中,图a是要分割的原图灰度图。
图b是人工标注的实例分割的标签数据。
图c是语义分割的GT(只有前景和背景两个类别)。但是对于细胞与细胞之间的区域,分割有一定困难。作者提出了pixel-wise lose weight的方案。在细胞与细胞之间的区域,施加一个更大的权重。而在大片的背景区域,则施加一个比较小的权重。
图d是在训练的时候GT每个像素所对应的权重热力图。可以看到细胞与细胞之间的区域基本都是红色,对应大权重;对于大片背景区域,都是蓝色,权重都是比较小的。
但是论文中作者并没有针对pixel-wise lose weight做相应的相融实验。
参考
- U-Net网络结构讲解
