小样本学习(Few-Shot Learning)(一)
1. 前言
本文讲解小样本学习(Few-Shot Learning)基本概念及基本思路,孪生网络(Siamese Network)基本原理及训练方法。
小样本学习(Few-Shot Learning)(二)讲解小样本学习问题的Pretraining+Fine Tuning解法。
小样本学习(Few-Shot Learning)(三)使用飞桨(PaddlePaddle)基于paddle.vision.datasets.Flowers数据集实践小样本学习问题的Pretraining+Fine Tuning解法。
本人全部文章请参见:博客文章导航目录
本文归属于:元学习系列
2. 小样本学习
1997年5月2日,小敏生日,在动物园游玩。小敏走进极地馆,发现了图一所示毛茸茸的可爱小动物,她非常喜欢,但是小敏之前没有见过,不知道它的名字。小敏拿出入园时领取的动物学识卡,逐一翻阅卡片,确定图一中的小动物是狐狸。

 小敏去动物园游玩之前没有见过狐狸,因此不可能认识图一中的小动物,但是她只需要看一下动物学识卡,就能学会辨认图一中小动物是狐狸。小敏可以做到,那么计算机是否也可以做到?
小敏去动物园游玩之前没有见过狐狸,因此不可能认识图一中的小动物,但是她只需要看一下动物学识卡,就能学会辨认图一中小动物是狐狸。小敏可以做到,那么计算机是否也可以做到?
或者说,如果训练集中每一类只有一两个样本,计算机能否做出像小敏一样正确的分类呢?
2.1. 基本概念
2.1.1 元学习(Meta Learning)
元学习的解释为学会学习(Learning to learn)。“学会”是指训练模型直至收敛,“学习”是指学习的能力。“学会学习”是指通过训练机器学习模型,使得其具备学习的能力。
元学习是人工智能领域的一个重要研究分支,是一切尝试让机器具备学习能力的理论和工程方法的统称。小样本学习是元学习的一个子领域。
如何理解【学习的能力】?
上述例子中,小敏没有见过狐狸,她作出图一中小动物是狐狸这一判断的依据是图一中的小动物和入园时领取的动物学识卡中的狐狸长得非常像,即小敏能够判断动物之间的异同。这种能够判断事物之间异同的能力就是一种【学习的能力】。
【学习的能力】远不止判断事物之间的异同这一种,但是在小样本学习领域,主要方法之一是通过训练深度学习模型,使其具备这种判断事物之间异同的能力,从而解决小样本学习问题。
2.1.2 Support Set和Query
将上述小敏学会辨认狐狸的例子抽象成小样本学习问题,由于小敏在进动物园游玩前没有见过狐狸,因此小敏不可能认识狐狸。小敏要知道图一中小动物的名字,必须有入园时领取的动物学识卡提供额外信息。
在小样本学习中,动物学识卡这种数据集被称为Support Set,图一这种需要判断其类别的图片被成为Query。根据Support Set中类别数量和样本数量的不同,Support Set可被称为 k k k-way n n n-shot Support Set。
- k k k-way:Support Set中存在 k k k个类别
- n n n-shot:每个类别中存在 n n n个样本
在上述小敏学会辨认狐狸的例子中,小敏入园时领取的动物学识卡构成的Support Set中有狐狸、松鼠、兔子、仓鼠、水獭和海狸6种不同的小动物,因此 k k k等于6。每种小动物卡片只有一张,所有 n n n等于1。这个Support Set是6-way 1-shot Support Set。
小样本分类准确率会受到Support Set中类别数量和样本数量的影响,随着类别数量增加,分类准确率会降低。随着每个类别样本数增加,分类会更准确。
Support Set与训练集的区别:
训练集是一个非常大的数据集,每一类均包含非常多张图片。训练集足够大,可以用来训练一个深度神经网络。Support Set非常小,每一类只包含一张或几张图片,不足以训练一个深度神经网络。Support Set用于在预测时提供额外信息,使得模型能够断出所属类别不在训练集中的Query图片的类别。
2.1.3 传统机器学习与小样本学习的区别
传统监督学习首先会在一个训练集上训练模型,模型训练好之后可以用来做预测,给定一张测试图片,模型预测该图片类别。测试图片不在训练集中,但是其归属于训练集中的某一类。
小样本学习与传统监督学习有所不同,小样本学习的目标不是让机器识别训练集中的图片并且泛化到测试集,小样本学习的目标是让机器自己学会学习。用一个很大的数据集训练神经网络,学习的目的不是让模型知道什么是狐狸什么是老鼠,从而能够识别没有见过的狐狸和老鼠。学习的目的是让模型理解事物的异同,学会区分不同的事物。给定两张图片,不是让模型识别两张图片是什么,而是让模型判断两张图片中的对象是否相同。
因为训练集中不包含测试样本及其类别,因此小样本学习比传统监督学习更难。
2.2 基本思路
在小样本学习问题中,Support Set中每一类往往只有少数几个样本,单单依靠这些样本,不可能训练出一个深度神经网络,甚至无法采用迁移学习中的Pretraining+Fine Tuning方法。即对于小样本学习问题,不能采用传统的监督学习方法来进行分类。
小样本学习的最基本想法是学习一个 s i m sim sim函数来判断相似度。给定两张图片 x x x和 x ′ x^\prime x′,如果两张图片越相似,则 s i m ( x , x ′ ) sim(x,x^\prime) sim(x,x′)的值越大。在理想情况下,若 x x x和 x ′ x^\prime x′属于同一类,则 s i m ( x , x ′ ) = 1 sim(x,x^\prime)=1 sim(x,x′)=1,若 x x x和 x ′ x^\prime x′属于不同类,则 s i m ( x , x ′ ) = 0 sim(x,x^\prime)=0 sim(x,x′)=0。
具体可以按照如下思路解决小样本学习问题:
- 在一个大数据集中学习一个判断两张图片相似程度的相似度函数;
- 给定一个Query图片,将其和Support Set中各图片逐一对比,计算相似度;
- 在Support Set中找到与Queryt图片相似度最高的图片,将其类别作为预测结果。
3. 孪生网络
前面提到解决小样本学习问题的思路之一是学习一个相似度函数,孪生网络就是断两张图片相似程度的深度神经网络,其使用同一个深度神经网络对两张输入图片 x 1 x_1 x1和 x 2 x_2 x2分别提取特征,得到 f ( x 1 ) f(x_1) f(x1)和 f ( x 2 ) f(x_2) f(x2),计算 f ( x 1 ) f(x_1) f(x1)和 f ( x 2 ) f(x_2) f(x2)之间的相似度并更新深度神经网络参数。预测时根据 f ( x q ) f(x_q) f(xq)和 f ( x s ) f(x_s) f(xs)之间的相似度判断给定Query图片的类别。
孪生网络用同一个网络分别从不同输出中提取特征,将得到的特征融合并判断输入之间的相似度。网络“身体”是分开的,“头”是相连的,因此命名为孪生网络。
3.1 训练孪生网络
3.1.1 Learning Pairwise Similarity Scores
训练孪生网络需要用到一个大的分类数据集,数据集中每张图片均有标注,每一类均包含许多张图片。训练的第一种方法是每次从数据集中随机抽取两个样本,比较他们的相似度,并根据相似度函数损失更新网络参数。
首先须使用数据集来构造正样本和负样本,其中正样本用于告诉神经网络什么东西是同一类,负样本用于告诉神经网络事物之间的区别。构造正样本首先须从数据集中随机抽取一张图片 x 1 x_1 x1,然后从同一类中随机抽取另一张图片 x 2 x_2 x2,形成三元组 ( x 1 , x 2 , 1 ) (x_1,x_2,1) (x1,x2,1)。构造负样本每次先随机抽取一张图片 x 1 ′ x_1^\prime x1′,然后排除 x 1 ′ x_1^\prime x1′的类别,从随机集中随机抽取另一张图片 x 2 ′ x_2^\prime x2′,形成三元组 ( x 1 ′ , x 2 ′ , 0 ) (x_1^\prime,x_2^\prime,0) (x1′,x2′,0)。重复上述构造正样本和负样本的过程,即可生成用于训练孪生网络的训练集。

搭建卷积神经网络用于提取图片中的特征,网络输入是一张图片 x x x,输出是提取的特征向量 f ( x ) f(x) f(x)。将生成的训练集中一个样本的两张图片 x 1 x_1 x1和 x 2 x_2 x2分别输入搭建的卷积神经网络,得到特征向量 h 1 h_1 h1和 h 2 h_2 h2。将向量 h 1 h_1 h1和 h 2 h_2 h2结合形成特征向量 z z z(如令 z = c o n c a t ( h 1 , h 2 ) z=concat(h_1,h_2) z=concat(h1,h2)或 z = ∣ h 1 − h 2 ∣ z=|h_1-h_2| z=∣h1−h2∣等等),然后用一些全连接层处理 z z z向量,输出一个标量,并将该标量经过 S i g m o i d Sigmoid Sigmoid激活函数,得到一个介于 0 ∼ 1 0\sim 1 0∼1之间的实数。
该实数可以衡量输入的两张图片 x 1 x_1 x1和 x 2 x_2 x2之间的相似度,如果 x 1 x_1 x1和 x 2 x_2 x2属于同一个类别,则输出实数应该接近于1,否则应该接近于0。使用网络输出与真实标签之间的交叉熵( C r o s s E n t r o p y CrossEntropy CrossEntropy)作为损失函数,通过反向传播计算模型参数的梯度,并使用梯度下降法来更新模型参数。

训练孪生网络需要准备数量大致相当的正样本和负样本,负样本是不同类别的两张图片,其标签为0,通过训练使孪生网络输出接近于0。
训练好孪生网络之后,可以用来做小样本分类。逐一对比Query图片与Support Set中的图片,返回Support Set中相似度最高的图片类别作为预测结果。
3.1.2 Triplet Loss
上述训练孪生网络方法从理论上看起来很完美,但是在深度学习实践中,上述方法效果并不是特别好。在深度学习领域,理论上看起来很完美,但是实际效果却一塌糊涂的例子数见不鲜,比上述方法更好的训练孪生网络的方法是使用Triplet Loss。
使用Triplet Loss,在构建训练集时,需每次从数据集中选取3张图片。首先从数据集中随机选取一张图片作为锚点(Anchor),再从锚点图片所在类别中随机抽取另一张图片作为正样本(Positive),然后排除锚点图片所在类别,从数据集中随机选取一张图片作为负样本(Negative)。
将锚点图片、正样本图片和负样本图片分别输入搭建好的用于提取图片特征的卷积神经网络,得到三个特征向量 f ( x + ) 、 f ( x a ) f(x^+)、f(x^a) f(x+)、f(xa)和 f ( x − ) f(x^-) f(x−)。分别计算 f ( x + ) f(x^+) f(x+)和 f ( x a ) f(x^a) f(xa)、 f ( x − ) f(x^-) f(x−)和 f ( x a ) f(x^a) f(xa) 二范数 的平方 d + d^+ d+和 d − d^- d−,即 d + = ∣ ∣ f ( x + ) − f ( x a ) ∣ ∣ 2 2 d^+=||f(x^+)-f(x^a)||_2^2 d+=∣∣f(x+)−f(xa)∣∣22, d − = ∣ ∣ f ( x a − f ( x − ) ) ∣ ∣ 2 2 d^-=||f(x^a-f(x^-))||_2^2 d−=∣∣f(xa−f(x−))∣∣22。

卷积神经网络能够把一张图片映射成特征空间中的一个点,为了解决小样本学习问题,我们期望训练好的神经网络能够将相同类别的图片在特征空间中对应点全部聚集在一起,将不同类别的图片在特征空间中对应的点分开。如图六所示,因为正样本和锚点属于同一类别,负样本和锚点属于不同类别,因此 d + d^+ d+应该很小, d − d^- d−应该很大。
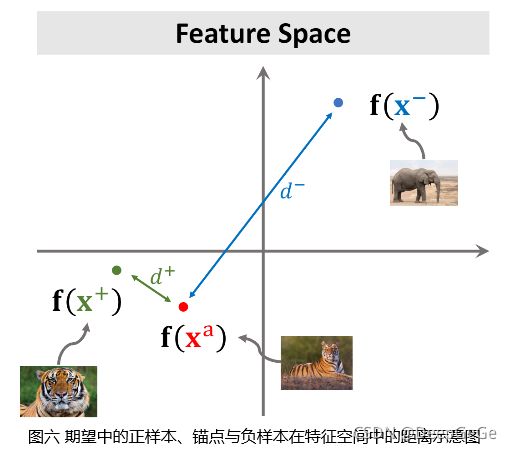
训练孪生网络的损失函数首先应该鼓励正样本在特征空间上接近锚点,即使 d + d^+ d+尽量小。其次应该鼓励负样本在特征空间上远离锚点,即使 d − d^- d−尽量大。因此,可分为如下两种情况:
- 如果 d − ⩾ d + + α d^-\geqslant d^++\alpha d−⩾d++α,可认为这一组样本分类正确, L o s s = 0 Loss=0 Loss=0;
- 假如上述条件不满足,说明模型无法区分该组正负样本, L o s s = d + + α − d − Loss=d^++\alpha-d^- Loss=d++α−d−。
即Triplet Loss可定义如下:
L o s s ( x a , x + , x − ) = m a x { 0 , d + + α − d − } Loss(x^a,x^+,x^-)=max\{0, d^++\alpha-d^-\} Loss(xa,x+,x−)=max{0,d++α−d−},其中 α \alpha α被称为间隔(Margin),是一个超参数。
确定损失函数之后,可以求损失函数关于模型参数的梯度,并使用随机梯度下降法更新模型参数。训练好孪生网络之后,可以通过如下方法来做小样本分类。
将Query图片和Support Set中所有图片全部转化为特征向量,然后依次计算Query图片对应的特征向量和Support Set中各图片对应特征向量之间的距离,返回Support Set中距离最小的图片类别作为预测结果。
4. 后记
经过数十年的发展,深度学习领域各种模型方法层出不穷,可以说没有任何人是深度学习所有领域的专家。在小样本学习领域,最近几年有很多论文发表,提出了上百种模型和方法。孪生网络并不是小样本学习问题最好的解决方法,但是最简单好用的方法思路均是Embedding,即将图片映射成特征向量,思路和孪生网络非常像。了解孪生网络原理有助于理解其他小样本学习方法。
小样本学习(Few-Shot Learning)(二)讲解小样本学习问题的Pretraining+Fine Tuning解法。
5. 参考资料链接
- https://www.youtube.com/watch?v=UkQ2FVpDxHg&list=PLvOO0btloRnuGl5OJM37a8c6auebn-rH2&index=1
- https://www.youtube.com/watch?v=Er8xH_k0Vj4&list=PLvOO0btloRnuGl5OJM37a8c6auebn-rH2&index=2
- https://github.com/wangshusen/DeepLearning/blob/master/Slides/16_Meta_1.pdf
- https://github.com/wangshusen/DeepLearning/blob/master/Slides/16_Meta_2.pdf