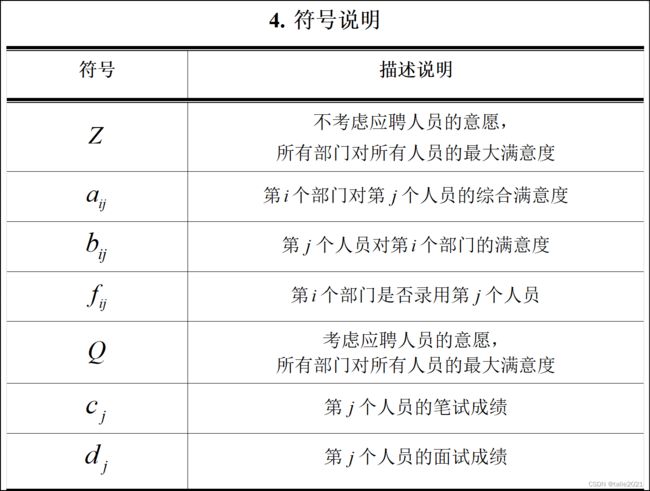
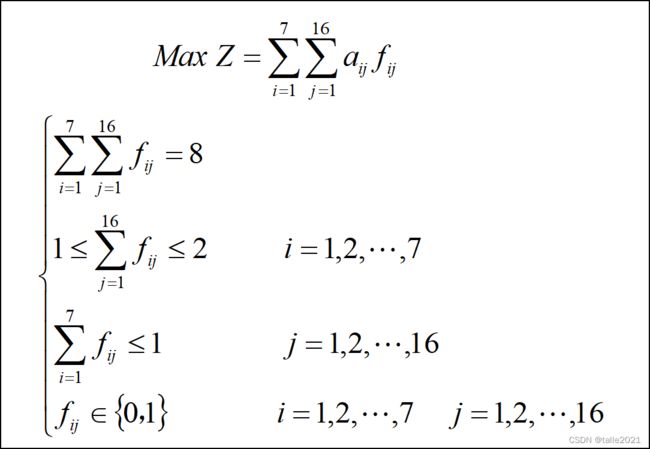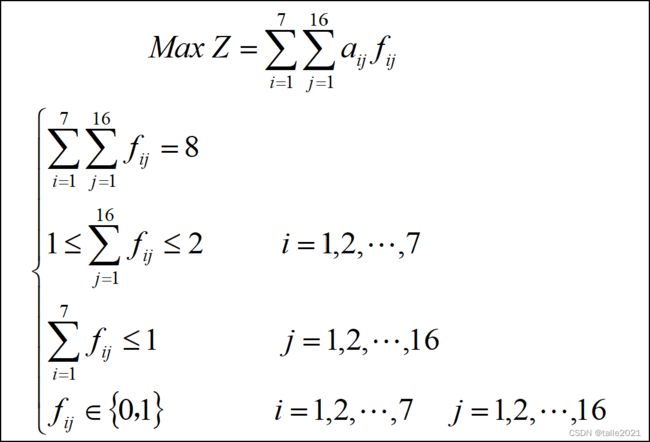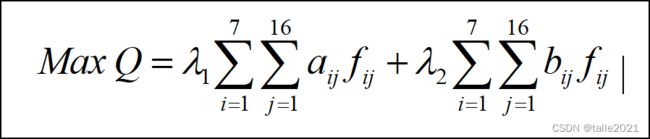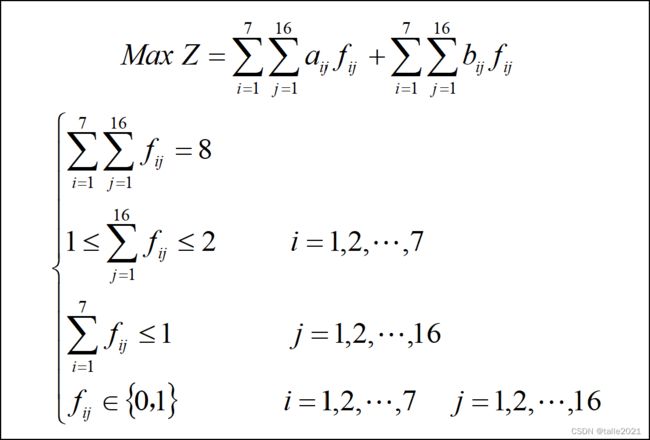数学建模——整数规划（0-1规划）问题

题目：现拟将录用的8名公务员安排到所属的7个部门，并且要求每个部门至少安排一名公员。

x招聘领导小组在确定录用名单的过程中，本着公平、公开的原则，同时考虑录用人员的合理分配和使用，有利于发挥个人的特长和能力。招聘领导小组将7个用人单位的基本情况（包括福利待遇、工作条件、劳动强度、晋升机会和学习深造机会等）和四类工作对聘用公务员的具体条件的希望达到的要求都向所有应聘人员公布（见表2）。每一位参加面试人员都可以申报两个自己的工作类别志愿（见表1）。请研究下列问题：

（1）如果不考虑应聘人员的意愿，择优按需录用，试帮助招聘领导小组设计一种录用分配方案；

（2）在考虑应聘人员意愿和用人部门的希望要求的情况下，请你帮助招聘领导小组设计一种分配方案；

表１：招聘公务员笔试成绩，专家面试评分及个人志愿　　　    

应聘 人员	笔试 成绩	申报类别志愿		专家组对应聘者特长的等级评分
				知识面	理解能力	应变能力	表达能力
人员1	290	（2）	（3）	A	A	B	B
人员2	288	（3）	（1）	A	B	A	C
人员3	288	（1）	（2）	B	A	D	C
人员4	285	（4）	（3）	A	B	B	B
人员5	283	（3）	（2）	B	A	B	C
人员6	283	（3）	（4）	B	D	A	B
人员7	280	（4）	（1）	A	B	C	B
人员8	280	（2）	（4）	B	A	A	C
人员9	280	（1）	（3）	B	B	A	B
人员10	280	（3）	（1）	D	B	A	C
人员11	278	（4）	（1）	D	C	B	A
人员12	277	（3）	（4）	A	B	C	A
人员13	275	（2）	（1）	B	C	D	A
人员14	275	（1）	（3）	D	B	A	B
人员15	274	（1）	（4）	A	B	C	B
人员16	273	（4）	（1）	B	A	B	C

表 2:　用人部门的基本情况及对公务员的期望要求

用人 部门	工作 类别	各用人部门的基本情况					各部门对公务员特长的希望达到的要求
		福利待遇	工作条件	劳动强度	晋升机会	深造机会	知识面	理解能力	应变能力	表达能力
部门1	（1）	优	优	中	多	少	B	A	C	A
部门2	（2）	中	优	大	多	少	A	B	B	C
部门3	（2）	中	优	中	少	多
部门4	（3）	优	差	大	多	多	C	C	A	A
部门5	（3）	优	中	中	中	中
部门6	（4）	中	中	中	中	多	C	B	B	A
部门7	（4）	优	中	大	少	多

 

问题一分析：根据国家公务员招聘标准，对笔试成绩和面试成绩分配1：1的权重，以及对笔试成绩和面试等级进行标准化处理，通过求应聘人员的面试等级与部门所要求面试等级之差，再根据面试满意度对照表（见表3）找到相应的面试满意度，运用MATLAB软件进行数据处理可求得各部门对应聘人员的满意度，最后结合题目的需求，建立“0-1”优化模型，利用软件求解。

模型的建立：

1）、 将应聘人员的笔试成绩/300，得：

应聘人员	笔试成绩	应聘人员	笔试成绩
人员1	0.9667	人员9	0.9333
人员2	0.9600	人员10	0.9333
人员3	0.9600	人员11	0.9267
人员4	0.9500	人员12	0.9233
人员5	0.9433	人员13	0.9167
人员6	0.9433	人员14	0.9167
人员7	0.9333	人员15	0.9133
人员8	0.9333	人员16	0.9100

2）、将字母等级评分标准化：

字母等级	数值
A	0.9
B	0.8
C	0.7
D	0.6

3）、对每个应聘人员特长的等级评分进行标准化，取面试的等级评分与各应聘人员的面试分数的差值，最后得到七种不同的差值，由于所得差值中包含负数，因此我们根据差值制定相应面试满意度（即面试成绩）对照表如下：

差值	0.3	0.2	0.1	0	-0.1	-0.2	-0.5
满意度	0.95	0.90	0.85	0.80	0.75	0.70	0.65

4）、通过满意度对照表，我们可以求得每个应聘人员的面试满意度如下表：

	部门1	部门2	部门3	部门4	部门5	部门6	部门7
人员1	0.8125	0.8250	0.825	0.8250	0.8250	0.8250	0.8250
人员2	0.8000	0.8125	0.8125	0.8125	0.8125	0.8125	0.8125
人员3	0.7625	0.7750	0.7750	0.7750	0.7750	0.7750	0.7750
人员4	0.8000	0.8125	0.8125	0.8125	0.8125	0.8125	0.8125
人员5	0.7875	0.8000	0.8000	0.8000	0.8000	0.8000	0.8000
人员6	0.7750	0.7875	0.7875	0.7875	0.7875	0.7875	0.7875
人员7	0.7875	0.8000	0.8000	0.8000	0.8000	0.8000	0.8000
人员8	0.8000	0.8125	0.8125	0.8125	0.8125	0.8125	0.8125
人员9	0.8000	0.8125	0.8125	0.8125	0.8125	0.8125	0.8125
人员10	0.7625	0.7750	0.7750	0.7750	0.7750	0.7750	0.7750
人员11	0.7625	0.7750	0.7750	0.7750	0.7750	0.7750	0.7750
人员12	0.7625	0.7750	0.7750	0.7750	0.7750	0.7750	0.7750
人员13	0.7625	0.7750	0.7750	0.7750	0.7750	0.7750	0.7750
人员14	0.7750	0.7875	0.7875	0.7875	0.7875	0.7875	0.7875
人员15	0.7875	0.8000	0.8000	0.8000	0.8000	0.8000	0.8000
人员16	0.7875	0.8000	0.8000	0.8000	0.8000	0.8000	0.8000

以上过程用matlab求解，代码如下：

% s1=xlsread('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','sheet1','B2:B17');
s2=xlsread('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','sheet1','C2:F17');
s3=xlsread('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','sheet1','K1:N7');
% disp(s3)
e=zeros(7,4);
%     for i=1:16
       for k=1:7       
            for j=1:4
                e(k,j)=s2(16,j)-s3(k,j);
                if (e(k,j)==3)
                    e(k,j)=0.95;
                    continue;
                end
                if (e(k,j)==2)
                    e(k,j)=0.9;
                    continue;
                end
                if (e(k,j)==1)
                    e(k,j)=0.85;
                    continue;
                end
                if (e(k,j)==0)
                    e(k,j)=0.8;
                    continue;
                end
                if (e(k,j)==-1)
                    e(k,j)=0.75;
                    continue;
                end
                if (e(k,j)==-2)
                    e(k,j)=0.70;
                    continue;
                end
                if (e(k,j)==-3)
                    e(k,j)=0.65;
                    continue;
                end
            end
       end
%     end

disp(e)
sum_row=sum(e,2);
disp((sum_row/4)');
xlswrite('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx',(sum_row/4)','sheet2','F17:L17');
% s1=s1/300;


% xlswrite('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx',s1,'sheet2','b2');
% xlswrite('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx',s3,'sheet2','c2');

s2=xlsread('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','sheet2','B2:B17');
s3=xlsread('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','sheet2','F2:L17');
e=zeros(16,7);
for i=1:16
    for j=1:7
        e(i,j)=s2(i,1)*0.5+s3(i,j)*0.5;
    end
end
disp(e);
xlswrite('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx',e,'sheet2','f22:l37');

接下来引入0-1变量：

根据约束条件分析，建立如下的数学模型：

 求解该模型则运用Lingo软件，代码如下：

model:
sets:
aa/1..7/;
bb/1..16/;
link(bb,aa):a,f;
endsets
data:
a=@ole('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','data');此处的‘data’在Excel设置，确定数据位置
！将f写入Excel
@ole('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','one')=f;此处的‘one’在Excel设置，确定写入位置
enddata
max=@sum(bb(i):@sum(aa(j):f(i,j)*a(i,j)));
@for(bb(i):@sum(aa(j):f(i,j))>=0);
@for(bb(i):@sum(aa(j):f(i,j))<=1);
@for(aa(j):@sum(bb(i):f(i,j))<=2);
@for(aa(j):@sum(bb(i):f(i,j))>=1);
@for(bb(i):@for(aa(j):@bin(f(i,j))));
@sum(bb(i):@sum(aa(j):f(i,j)))=8;
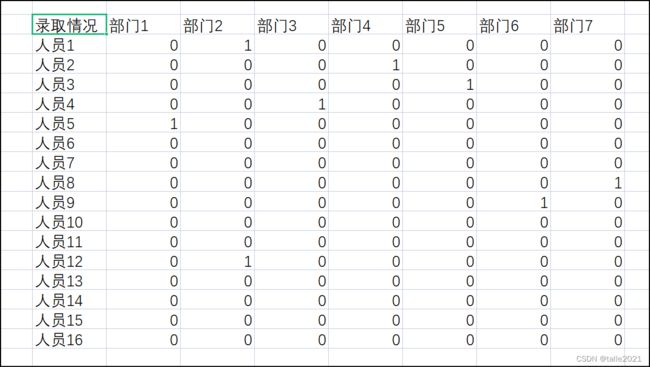
end

写入 Excel表如下：

 因此得到最终答案为：

用人部门	分配人员
1	人员5
2	人员1、人员12
3	人员4
4	人员2
5	人员3
6	人员9
7	人员8

问题二分析：

1）、我们的目标是需要使各部门对应聘人员的综合满意度达到最大值的同时，也需要让应聘人员的意愿（即满意度）达到最大值，因此我们对两个满意度分别分配1：1的权重，建立目标模型如下：

2）、 对应聘人员对第一、第二志愿以及其它工作类别的满意度进行标准化处理，结果如下表所示:

第一志愿	0.9
第二志愿	0.7
其它工作类别	0.4

3）、模型的建立：

 求解该模型则运用Lingo软件，代码如下：

model:
sets:
aa/1..7/;
bb/1..16/;
link(bb,aa):a,f,c;
endsets
data:
a=@ole('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','data');
c=@ole('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','point');
@ole('F:\数学建模算法与应用\公务员招聘\公务员分数.xlsx','zero')=f;
enddata
max=(@sum(bb(i):@sum(aa(j):f(i,j)*a(i,j)))+@sum(bb(i):@sum(aa(j):f(i,j)*c(i,j))));
@for(bb(i):@sum(aa(j):f(i,j))>=0);
@for(bb(i):@sum(aa(j):f(i,j))<=1);
@for(aa(j):@sum(bb(i):f(i,j))<=2);
@for(aa(j):@sum(bb(i):f(i,j))>=1);
@for(bb(i):@for(aa(j):@bin(f(i,j))));
@sum(bb(i):@sum(aa(j):f(i,j)))=8;
end

写入 Excel表如下：

  因此得到最终答案为：

用人部门	分配人员
1	人员9
2	人员8
3	人员1
4	人员5
5	人员2、人员12
6	人员7
7	人员4

PS:将Lingo结果写入Excel中，需对Excel设置，设置如下：

选定数据写入的合适区域，点击“公式”-“名称管理器”-“新建名称”，此时就可自定义名称啦