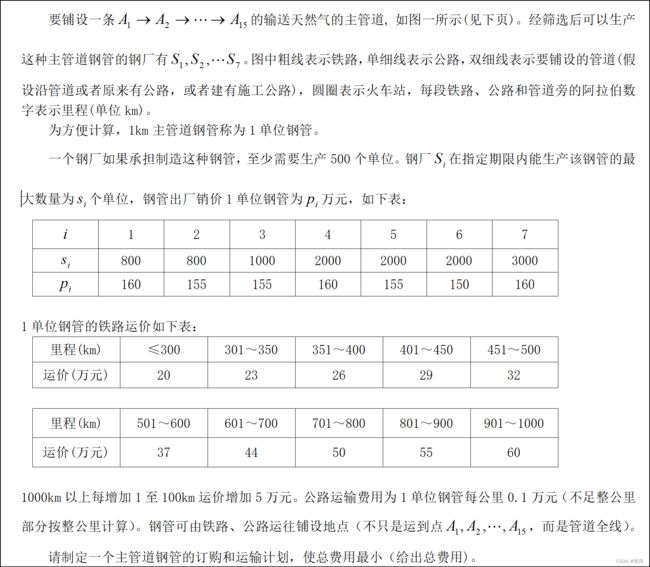
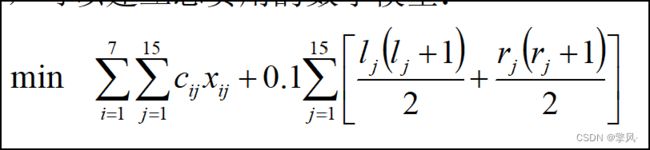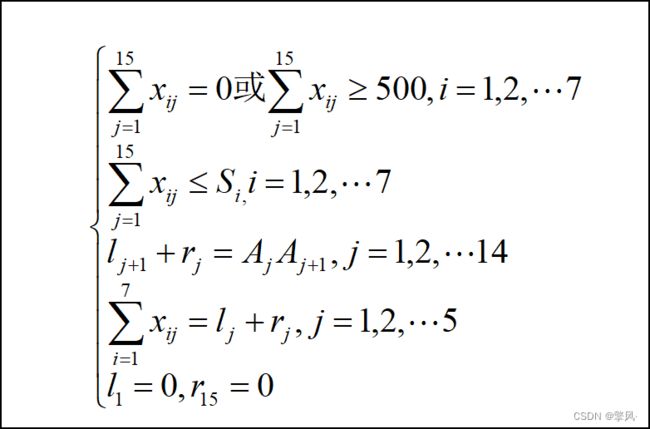最短路+最小费用+线性规划（钢管订购和运输问题）

钢管订购和运输问题题目详情：

 分析：解决本题首先计算运输一单位钢管的费用（最短路），再根据题目的约束条件求得钢管量（0-1规划）。

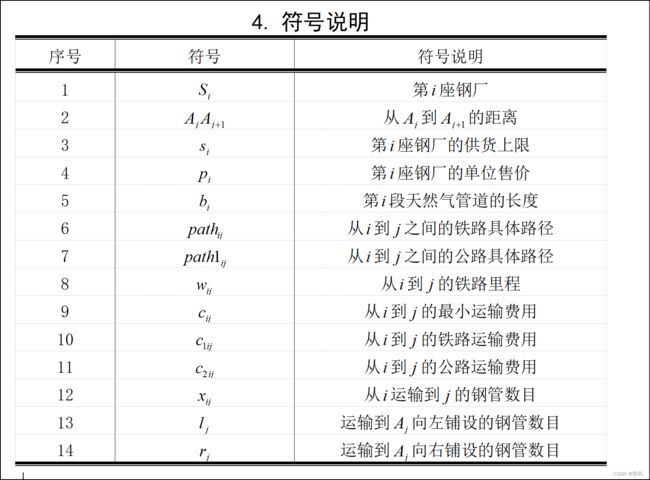
符号说明：

 

1.求最小运费

（1）构造铁路任意两点间的最小运输费用赋权图

        首先用Floyd算法构造铁路距离赋权图，接着计算两点间最短铁路距离值，再根据题目给出的铁路运价表，得到任意两点间的最小铁路费用。构造铁路距离矩阵c1（matlab代码如下：）

%w为铁路距离矩阵，c1为铁路费用矩阵
w=zeros(39,39);c=zeros(39,39);c2=zeros(39,39);
w(1,29)=20;w(1,30)=202;w(2,30)=1200;w(3,31)=690;w(4,34)=690;w(5,33)=462;
w(6,38)=70;w(7,39)=30;w(23,25)=450;w(24,25)=80;w(25,27)=1150;
w(26,28)=306;w(27,30)=1100;w(28,29)=195;w(30,31)=720;w(31,32)=520;
w(32,34)=170;w(33,34)=88;w(34,36)=160;w(35,36)=70;w(36,37)=320;
w(37,38)=160;w(38,39)=290;
w=w+w';%构造铁路距离邻接矩阵
for i=1:39
    for j=1:39
        if(i~=j)&& w(i,j)==0
            w(i,j)=200000000;%无铁路连接时，元素为充分大的数
        end
    end
end
for k=1:39
    for i=1:39
        for j=1:39
            if w(i,j)>w(i,k)+w(k,j)
                w(i,j)=w(i,k)+w(k,j);%求最短路径

            end
        end
    end
end
c1=w;
for i=1:39
    for j=1:39
        if c1(i,j)==0 
            c1(i,j)=0;
        end
        if c1(i,j)>0 && c1(i,j)<=300
            c1(i,j)=20;
        end
        if c1(i,j)>300 && c1(i,j)<=350
            c1(i,j)=23;
        end
        if c1(i,j)>350 && c1(i,j)<=400
            c1(i,j)=26;
        end
        if c1(i,j)>400 && c1(i,j)<=450
            c1(i,j)=29;
        end
        if c1(i,j)>450 && c1(i,j)<=500
            c1(i,j)=32;
        end
        if c1(i,j)>500 && c1(i,j)<=600
            c1(i,j)=37;
        end
        if c1(i,j)>600 && c1(i,j)<=700
            c1(i,j)=44;
        end
        if c1(i,j)>700 && c1(i,j)<=800
            c1(i,j)=50;
        end
        if c1(i,j)>800 && c1(i,j)<=900
            c1(i,j)=55;
        end
        if c1(i,j)>900 && c1(i,j)<=1000
            c1(i,j)=60;
        end
        %当距离大于1000时，特别注意临界值！！！
        if c1(i,j)>1000 && rem(c1(i,j),100)==0
            c1(i,j)=(floor((c1(i,j)-1000)/100))*5+60;
        end
        if c1(i,j)>1000 && rem(c1(i,j),100)~=0
            c1(i,j)=(floor((c1(i,j)-1000)/100))*5+65;
        end
    end
end

（2）构造铁路任意两点间的最小运输费用赋权图

        首先用Floyd算法构造公路距离赋权图，接着计算两点间最短公路距离值，再根据题目给出的公路运价表，得到任意两点间的最小公路费用。构造公路距离矩阵c2（matlab代码如下）

c2(1,14)=31;c2(6,21)=110;c2(7,22)=20;c2(8,9)=104;c2(9,10)=301;c2(9,23)=3;
c2(10,11)=750;c2(10,24)=2;c2(11,12)=606;c2(11,27)=600;c2(12,13)=194;
c2(12,26)=10;c2(13,14)=205;c2(13,28)=5;c2(14,15)=201;c2(14,29)=10;
c2(15,16)=680;c2(15,30)=12;c2(16,17)=480;c2(16,31)=42;c2(17,18)=300;
c2(17,32)=70;c2(18,19)=220;c2(18,33)=10;c2(19,20)=210;c2(19,35)=10;
c2(20,21)=420;c2(20,37)=62;c2(21,22)=500;c2(21,38)=30;c2(22,39)=20;
c2=c2+c2';
for i=1:39
    for j=1:39
        if(i~=j)&&c2(i,j)==0
            c2(i,j)=200000000;%无公路连接是为充分大的元素
        end
    end
end
for k=1:39
    for i=1:39
        for j=1:39
            if c2(i,j)>c2(i,k)+c2(k,j)
                c2(i,j)=c2(i,k)+c2(k,j);%求最短路径
            end
        end
    end
end
c3=c2;%公路距离矩阵
c2=0.1*c2;%求公路费用矩阵

（3）计算任意两点间的最小运输费用

        由于钢管可以用铁路和公路交叉运送，所以任意两点间的最小运输费用为铁路、公路两者最小运输费用的最小值，c=min{c1,c2}

for i=1:39
    for j=1:39
        if c1(i,j)c2(i,j)
            c(i,j)=c2(i,j);
        end
        if c1(i,j)==c2(i,j)
            c(i,j)=c2(i,j);
        end
    end
end
for i=1:39
    for j=1:39
        for k=1:39
            if c(i,j)>c(i,k)+c(k,j)
                c(i,j)=c(i,k)+c(k,j);
                path2(i,j)=k;
            end
        end
    end
end
for i=1:39
    for j=1:39
        if (i<=7)&&(j>=8)&&(j<=22)
            cf(i,j-7)=c(i,j);%从钢厂到管道节点的距离矩阵
        end
    end
end

     最终求得最小运费结果：

	单位钢管从钢厂S(i)运输到A(I)的运输费用
	A(1)	A(2)	A(3)	A(4)	A(5)	A(6)	A(7)	A(8)	A(9)	A(10)	A(11)	A(12)	A(13)	A(14)	A(15)
S(1)	170.7	160.3	140.2	98.6	38	20.5	3.1	21.2	64.2	92	96	106	121.2	128	142
S(2)	215.7	205.3	190.2	171.6	111	95.5	86	71.2	114.2	142	146	156	171.2	178	192
S(3)	230.7	220.3	200.2	181.6	121	105.5	96	86.2	48.2	82	86	96	111.2	118	132
S(4)	260.7	250.3	235.2	216.6	156	140.5	131	116.2	84.2	62	51	61	76.2	83	97
S(5)	255.7	245.3	225.2	206.6	146	130.5	121	111.2	79.2	57	33	51	71.2	73	87
S(6)	265.7	255.3	235.2	216.6	156	140.5	131	121.2	84.2	62	51	45	26.2	11	28
S(7)	275.7	265.3	245.2	226.6	166	150.5	141	131.2	99.2	77	66	56	38.2	26	2

在得到最小运费后，利用0-1规划，求最小费用（运费+钢管费+铺设费）模型：

 

由此，我们可建立目标模型如下：（注：此处的c应为cf，cf=c+p）写错啦emmm……

 

约束条件：

根据该模型求解（lingo代码在文末）

最终求得钢管订购的数据如表：

	单位钢管从钢厂S(i)运输到A(I)的运输量
	A(1)	A(2)	A(3)	A(4)	A(5)	A(6)	A(7)	A(8)	A(9)	A(10)	A(11)	A(12)	A(13)	A(14)	A(15)
S(1)	0	0	0	335	0	200	265	0	0	0	0	0	0	0	0	800
S(2)	0	179	188	133	0	0	0	300	0	0	0	0	0	0	0	800
S(3)	0	0	320	0	16	0	0	0	664	0	0	0	0	0	0	1000
S(4)	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S(5)	0	0	0	0	600	0	0	0	0	0	415	0	0	0	0	1015
S(6)	0	0	0	0	0	0	0	0	0	351	0	86	333	621	165	1556
S(7)	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

即厂家S1往A4节点运输335单位钢管，往A6节点运输200单位钢管，往A7节点运输265单位钢管，共计800单位。其它钢厂以此类推…………最小费用为127.8632亿元。

总结：这道题目解题代码

代码1（matlab）

s=[800 800 1000 2000 2000 2000 3000];
path=zeros(39,39);
path1=zeros(39,39);
path2=zeros(39,39);
cf=zeros(7,15);
w=zeros(39,39);c=zeros(39,39);c2=zeros(39,39);
w(1,29)=20;w(1,30)=202;w(2,30)=1200;w(3,31)=690;w(4,34)=690;w(5,33)=462;
w(6,38)=70;w(7,39)=30;w(23,25)=450;w(24,25)=80;w(25,27)=1150;
w(26,28)=306;w(27,30)=1100;w(28,29)=195;w(30,31)=720;w(31,32)=520;
w(32,34)=170;w(33,34)=88;w(34,36)=160;w(35,36)=70;w(36,37)=320;
w(37,38)=160;w(38,39)=290;
w=w+w';
for i=1:39
    for j=1:39
        if(i~=j)&& w(i,j)==0
            w(i,j)=200000000;
        end
    end
end
for k=1:39
    for i=1:39
        for j=1:39
            if w(i,j)>w(i,k)+w(k,j)
                w(i,j)=w(i,k)+w(k,j);
                path(i,j)=k;
            end
        end
    end
end
c1=w;
for i=1:39
    for j=1:39
        if c1(i,j)==0 
            c1(i,j)=0;
        end
        if c1(i,j)>0 && c1(i,j)<=300
            c1(i,j)=20;
        end
        if c1(i,j)>300 && c1(i,j)<=350
            c1(i,j)=23;
        end
        if c1(i,j)>350 && c1(i,j)<=400
            c1(i,j)=26;
        end
        if c1(i,j)>400 && c1(i,j)<=450
            c1(i,j)=29;
        end
        if c1(i,j)>450 && c1(i,j)<=500
            c1(i,j)=32;
        end
        if c1(i,j)>500 && c1(i,j)<=600
            c1(i,j)=37;
        end
        if c1(i,j)>600 && c1(i,j)<=700
            c1(i,j)=44;
        end
        if c1(i,j)>700 && c1(i,j)<=800
            c1(i,j)=50;
        end
        if c1(i,j)>800 && c1(i,j)<=900
            c1(i,j)=55;
        end
        if c1(i,j)>900 && c1(i,j)<=1000
            c1(i,j)=60;
        end
        if c1(i,j)>1000 && rem(c1(i,j),100)==0
            c1(i,j)=(floor((c1(i,j)-1000)/100))*5+60;
        end
        if c1(i,j)>1000 && rem(c1(i,j),100)~=0
            c1(i,j)=(floor((c1(i,j)-1000)/100))*5+65;
        end
    end
end
c2(1,14)=31;c2(6,21)=110;c2(7,22)=20;c2(8,9)=104;c2(9,10)=301;c2(9,23)=3;
c2(10,11)=750;c2(10,24)=2;c2(11,12)=606;c2(11,27)=600;c2(12,13)=194;
c2(12,26)=10;c2(13,14)=205;c2(13,28)=5;c2(14,15)=201;c2(14,29)=10;
c2(15,16)=680;c2(15,30)=12;c2(16,17)=480;c2(16,31)=42;c2(17,18)=300;
c2(17,32)=70;c2(18,19)=220;c2(18,33)=10;c2(19,20)=210;c2(19,35)=10;
c2(20,21)=420;c2(20,37)=62;c2(21,22)=500;c2(21,38)=30;c2(22,39)=20;
c2=c2+c2';
for i=1:39
    for j=1:39
        if(i~=j)&&c2(i,j)==0
            c2(i,j)=200000000;
        end
    end
end
for k=1:39
    for i=1:39
        for j=1:39
            if c2(i,j)>c2(i,k)+c2(k,j)
                c2(i,j)=c2(i,k)+c2(k,j);
                path1(i,j)=k;
            end
        end
    end
end
c3=c2;
c2=0.1*c2;
for i=1:39
    for j=1:39
        if c1(i,j)c2(i,j)
            c(i,j)=c2(i,j);
        end
        if c1(i,j)==c2(i,j)
            c(i,j)=c2(i,j);
        end
    end
end
for i=1:39
    for j=1:39
        for k=1:39
            if c(i,j)>c(i,k)+c(k,j)
                c(i,j)=c(i,k)+c(k,j);
                path2(i,j)=k;
            end
        end
    end
end
for i=1:39
    for j=1:39
        if (i<=7)&&(j>=8)&&(j<=22)
            cf(i,j-7)=c(i,j);
        end
    end
end
% xlswrite('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx',cf,'sheet1','b3:p9');
% xlswrite('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx',w,'sheet2','b4:AN42');
% xlswrite('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx',c1,'sheet2','b54:AN92');
% xlswrite('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx',c3,'sheet3','b4:AN42');
% xlswrite('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx',c2,'sheet3','b54:AN92');
% xlswrite('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx',c,'sheet4','b4:AN42');

代码2（Lingo）

model:
sets:
aa/1..7/:f,p,s;
bb/1..15/:l,r,a,b;
link(aa,bb):cf,x;
endsets
data:
p=160 155 155 160 155 150 160;
s=800 800 1000 2000 2000 2000 3000;
b=104 301 750 606 194 205 201 680 480 300 220 210 420 500 0;
！从文件中导出数据
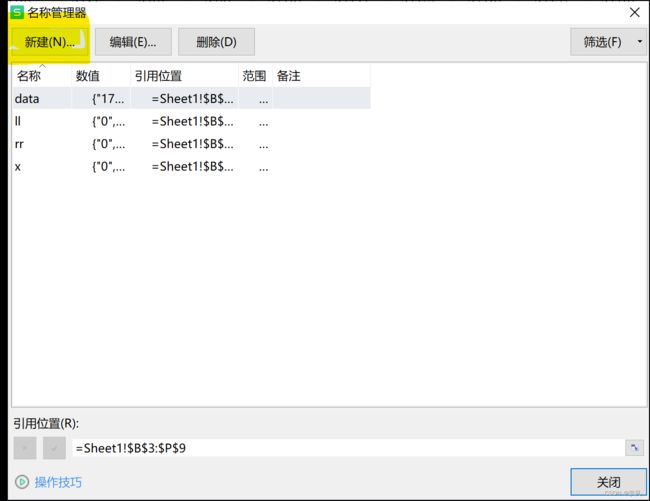
cf=@ole('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx','data');！data为Excel表的数据，此处需提前在Excel表中设置
设置过程参考下方步骤
！写入文件  注：x,ll,rr需在Excel表中提前设置
@ole('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx','x')=x;
@ole('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx','ll')=l;
@ole('F:\第三道问题：钢管运输问题\钢管运输问题1.xlsx','rr')=r;
enddata
min=@sum(link(i,j):(cf(i,j)+p(i))*x(i,j))+0.05*@sum(bb(j):l(j)^2+l(j)+r(j)^2+r(j));
@for(aa(i):@sum(bb(j):x(i,j))>=500*f(i));
@for(aa(i):@sum(bb(j):x(i,j))<=s(i)*f(i));
@for(bb(j):@sum(aa(i):x(i,j))=l(j)+r(j));
@for(bb(j)|j#ne#15:r(j)+l(j+1)=b(j));
l(1)=0;r(15)=0;
@for(aa:@bin(f));
@for(bb:@gin(l));
end

PS:Lingo将Excel表中数据导出或将数据写入Excel表，需对Excel表提前设置单元格名称，设置步骤如下：

选定数据写入的合适区域，点击“公式”-“名称管理器”-“新建”名称，此时就可自定义名称啦