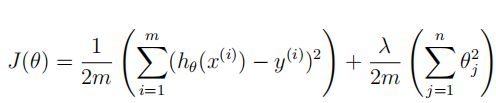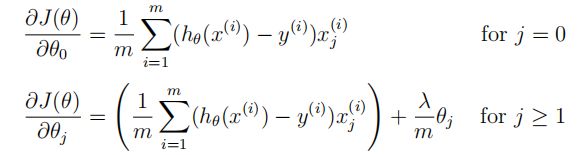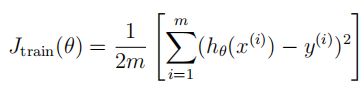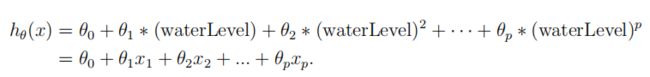吴恩达机器学习作业5:偏差和方差(Python实现)
机器学习练习 5 - Regularized Linear Regression and Bias v.s.Variance
Introduction
在本练习中,将实现正则化线性回归,并使用它来研究具有不同偏差-方差的模型。
1 Regularized Linear Regression(正则线性回归)
在练习的前半部分,将实现正则化的线性回归,利用水库水位的变化来预测从大坝流出的水量。在后半部分,将通过调试学习算法的参数,检查参数对偏差和方差的影响。
1.1 Visualizing the dataset(可视化数据集)
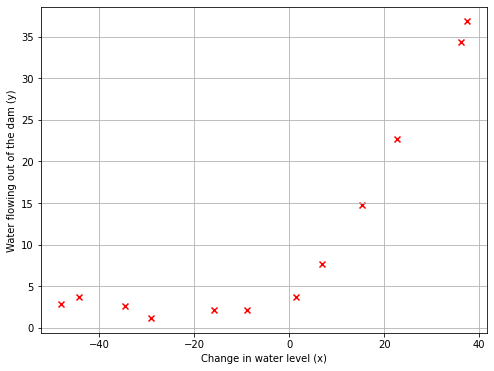
首先可视化:水位变化(x)和从大坝流出的水量的历史记录(y) 的数据集。
该数据集可分为三个部分:
- training set 训练集(
X,y):训练模型 - cross validation set 交叉验证集(
Xval,yval):选择正则化参数 - test set 测试集(
Xtest,ytest):评估性能(在训练过程中没有出现的数据)
在下面的实验中:首先绘制训练数据,然后实现线性回归,并使用它拟合一条直线并绘制学习曲线,接下来,实现多项式回归,以找到一个更好的适合于的数据。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
import scipy.optimize as opt
def load_mat(path):
data=loadmat(path)
X,y=data['X'],data['y']
Xval,yval=data['Xval'],data['yval']
Xtest,ytest=data['Xtest'],data['ytest']
X=np.insert(X,0,1,axis=1)
Xval=np.insert(Xval,0,1,axis=1)
Xtest=np.insert(Xtest,0,1,axis=1)
return X,y,Xval,yval,Xtest,ytest
path="ex5data1.mat"
X,y,Xval,yval,Xtest,ytest=load_mat(path)
X.shape,y.shape,Xval.shape,yval.shape,Xtest.shape,ytest.shape
((12, 2), (12, 1), (21, 2), (21, 1), (21, 2), (21, 1))
def PlotData(X,y,Line=0,fit_theta=[]):
fix,ax=plt.subplots(figsize=(8,6))
ax.scatter(X[:,1:],y[:,:],c='r',marker='x')
ax.set_xlabel("Change in water level (x)")
ax.set_ylabel("Water flowing out of the dam (y)")
ax.grid(True)
if(Line):
ax.plot(X[:,1],X@fit_theta)
# plt.show()
PlotData(X,y)
1.2 Regularized linear regression cost function(正则化线性回归的成本函数)
正则化的线性回归的成本函数:
其中, λ \lambda λ是一个控制正则化程度的正则化参数(防止过拟合)。正则化项对总体成本 J J J进行了惩罚,随着模型参数 θ j \theta_j θj的大小的增加,惩罚也会增加。(不需要惩罚 θ 0 \theta_0 θ0)
接下来编写一个函数CostReg:来计算正则化的线性回归成本函数。尝试向量化代码,避免使用循环。 θ \theta θ向量初始化为 [ 1 ; 1 ] [1;1] [1;1], λ \lambda λ初始化为 1 1 1,成本函数正确答案应该约为 303.993 303.993 303.993。
def CostReg(theta,X,y,l=1):
cost=(np.sum((X@theta-y.flatten())**2)+np.sum(theta[1:]**2)*l)/(2*len(X))
return cost
theta=np.ones(X.shape[1])
theta.shape
(2,)
CostReg(theta, X, y,1)
303.9931922202643
1.3 Regularized linear regression gradient(正则化的线性回归梯度)
θ j \theta_j θj的正则化线性回归代价函数的偏导数被定义为:
接下来编写函数GradientReg,来计算梯度, θ \theta θ向量初始化为 [ 1 ; 1 ] [1;1] [1;1], λ \lambda λ初始化为 1 1 1,最终运行出来的梯度约为 [ − 15.30 ; 598.250 ] [-15.30;598.250] [−15.30;598.250]
def GradientReg(theta,X,y,l=1):
grad = (X@theta-y.flatten())@X #([email protected]())结果是(12,),而X是(12,2),希望X中每一列分别与前面的结果点乘,然后形成新的向量
theta[0] = 0
theta = l*theta
(grad+theta)/len(X)
return (grad+theta)/len(X)
GradientReg(theta,X,y,1)
array([-15.30301567, 598.25074417])
1.4 Fitting linear regression(线性回归拟合)
现在成本函数CostReg和梯度函数GradientReg完成了,接下来就是计算出最优的 θ \theta θ。使用fmincg来优化成本函数。
在这一部分中,将正则化参数 λ \lambda λ设为 0 0 0,因为目前实现的线性回归在试图拟合一个二维的 θ \theta θ,正则化对于低维的 θ \theta θ不会有太大的帮助。在后面的实验中,将使用带有正则化的多项式回归。
def TrainLinearReg(X,y,l):
theta=np.zeros(X.shape[1])
res=opt.minimize(fun=CostReg,x0=theta,args=(X,y,l),method='TNC',jac=GradientReg)
return res.x
fit_theta=TrainLinearReg(X,y,0)
fit_theta
array([13.08790351, 0.36777923])
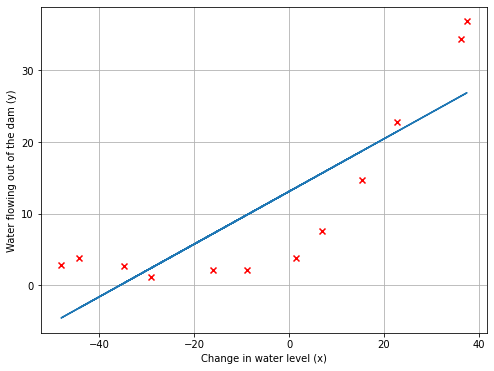
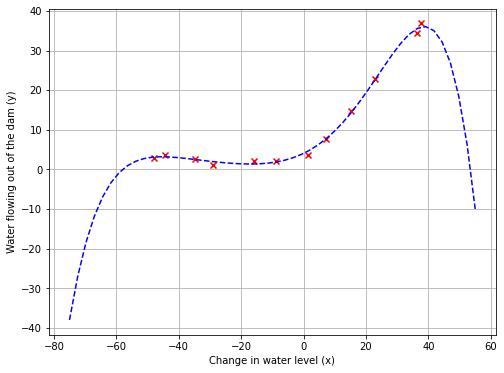
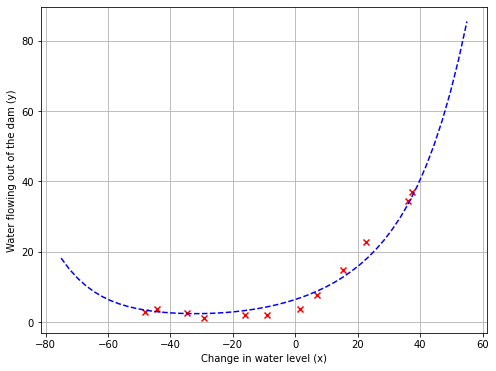
PlotData(X,y,1,fit_theta)
最佳拟合线表明:此模型不适用于该数据,因为该数据具有非线性的性质。虽然可视化最佳拟合是调试学习算法的一种方法,但可视化数据和模型有时是比较困难的。在下一节中,将实现一个函数来生成学习曲线,它可以帮助调试学习算法,即使可视化数据比较困难。
2 Bias-variance(偏差-方差)
机器学习中的一个重要概念就是偏差-方差权衡。高偏差意味着欠拟合;高方差意味着过拟合。在这部分的实验中,将在学习曲线上绘制训练误差和验证误差,以诊断偏差-方差问题。
2.1 Learning curves(学习曲线)
现在将实现代码来生成学习曲线,这对调试学习算法有很大作用。一条学习曲线将训练误差和交叉验证误差作为训练集大小的函数绘制出来。接下来的实验就是实现学习曲线的代码编写。
为了绘制学习曲线,训练样本X从 1 1 1开始逐渐增加,训练出不同的参数向量 θ \theta θ,接着通过交叉验证样本Xval计算验证误差:
- 使用训练集的不同子集来训练模型,得到不同的 θ \theta θ
- 通过 θ \theta θ计算训练误差和交叉验证误差,此时不要使用正则化(训练误差不包括正则化项),并且此时 λ = 0 \lambda=0 λ=0(使用现有的成本函数
CostReg来计算误差,并且设置 λ = 0 \lambda=0 λ=0) - 计算训练集误差时,请确保在训练子集上计算(即 X [ 0 : i , : ] , y [ 0 : i ] X[0:i,:],y[0:i] X[0:i,:],y[0:i],而不是整个训练集);计算交叉验证误差时,在整个交叉验证集来计算,无需分为子集。将计算出的误差分别存储在向量
error_train和error_val中。
一个训练集的训练误差公式:
def plot_learning_curve(X,y,Xval,yval,l):
size = range(1, len(X)+1)
error_train, error_val = [], []
for i in size:
i_theta = TrainLinearReg(X[:i, :], y[:i], l)
i_train_cost = CostReg(i_theta, X[:i, :], y[:i], 0)
i_val_cost = CostReg(i_theta, Xval, yval)
error_train.append(i_train_cost)
error_val.append(i_val_cost)
fix, ax = plt.subplots(figsize=(8, 6))
ax.plot(size,error_train,label="Train",color="blue")
ax.plot(size,error_val,label="Cross Validation",color="green")
ax.legend()
ax.set_xlabel("Number of training examples")
ax.set_ylabel("Error")
ax.set_title("Learning curve for linear regression")
ax.grid(True)
plt.show()
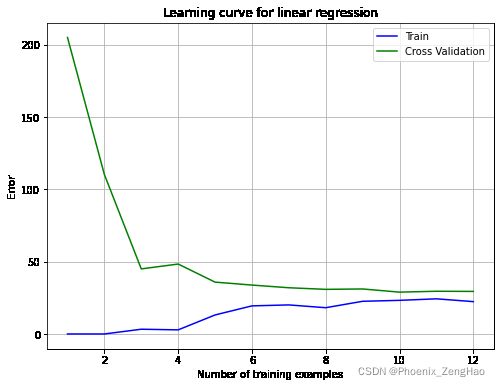
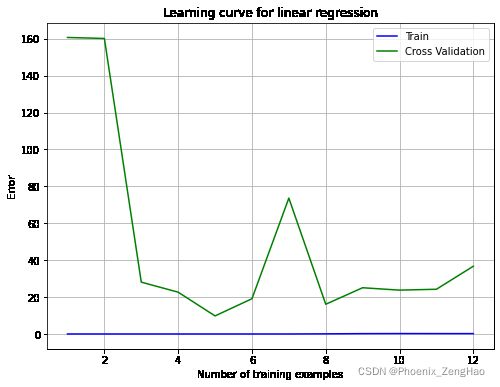
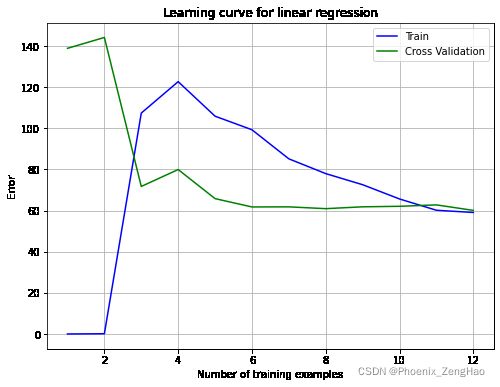
plot_learning_curve(X, y, Xval, yval, 0)
从图中可以看出来,随着样本数量的增加,训练误差和交叉验证误差都很高,这属于高偏差,欠拟合。该线性回归模型太简单了,不适合应用在此数据集上。在下一节实验中,将实现多项式回归模型。
3 Polynomial regression(多项式回归)
线性回归模型存在的问题是它对数据来说太简单了,导致了欠拟合(高偏差)。在本部分的实验中,将通过添加更多的特性来解决这个问题。使用多项式回归,假设函数形式:
假设 x 1 = w a t e r L e v e l , x 2 = ( w a t e r L e v e l ) 2 , . . . , x p = ( w a t e r L e v e l ) p x_1=waterLevel,x_2=(waterLevel)^2,...,x_p=(waterLevel)^p x1=waterLevel,x2=(waterLevel)2,...,xp=(waterLevel)p,从而得到了一个线性回归模型,其中特征是原始值(水位)的不同幂。
现在使用数据集中现有特征x的不同次幂来添加更多特性。所以接下来的实验要求就是奖训练集中的X( m × 1 m\times 1 m×1)映射到更高次幂。具体来讲,将训练集X( m × 1 m\times 1 m×1)作为参数传递到函数,那么函数需要返回一个矩阵X_poly( m × p m\times p m×p),其中第 1 1 1列保存了 X X X,第 2 2 2列保存了 X 2 X^2 X2,…,第 p p p列保存了 X p X^p Xp。
def X_poly_features(X,power):#X需要时ndarray类型,不可以是matrix类型
X=X[:,1:].flatten() #取出X的第二列的所有元素(即最初的X)然后展开成一维数组
data={'f{}'.format(i):np.power(X,i) for i in range(0,power+1)}
df=pd.DataFrame(data)
return df
X_poly_features(X, power=3)
| f0 | f1 | f2 | f3 | |
|---|---|---|---|---|
| 0 | 1.0 | -15.936758 | 253.980260 | -4047.621971 |
| 1 | 1.0 | -29.152979 | 849.896197 | -24777.006175 |
| 2 | 1.0 | 36.189549 | 1309.683430 | 47396.852168 |
| 3 | 1.0 | 37.492187 | 1405.664111 | 52701.422173 |
| 4 | 1.0 | -48.058829 | 2309.651088 | -110999.127750 |
| 5 | 1.0 | -8.941458 | 79.949670 | -714.866612 |
| 6 | 1.0 | 15.307793 | 234.328523 | 3587.052500 |
| 7 | 1.0 | -34.706266 | 1204.524887 | -41804.560890 |
| 8 | 1.0 | 1.389154 | 1.929750 | 2.680720 |
| 9 | 1.0 | -44.383760 | 1969.918139 | -87432.373590 |
| 10 | 1.0 | 7.013502 | 49.189211 | 344.988637 |
| 11 | 1.0 | 22.762749 | 518.142738 | 11794.353058 |
3.1 Learning Polynomial Regression(多项式回归)
请记住,即使在特征向量中有多项式项,但实际上仍然在解决线性回归优化问题。多项式项已经变成了可以用于线性回归的特征。成本函数CostReg和梯度函数GradientReg保持不变。
对于这部分的实验,将使用一个 8 8 8次的多项式。但是,如果直接在投影数据上运行训练,显然不能很好地拟合,因为特征会被严重地扩展(比如, x = 40 x=40 x=40,那么就会产生新的特征值 x 8 = 4 0 8 = 6.5 ∗ 1 0 12 x_8=40^8=6.5*10^{12} x8=408=6.5∗1012),因此,需要使用特征归一化。
在学习多项式回归的参数 θ \theta θ之前,首先调用函数featureNormalize(将在接下来的实验中实现)对特征进行标准化,并对训练集的特征进行归一化,分别存储均值,标准差变量。
接下来实现函数get_means_std:获取训练集的均值和误差,用来标准化所有数据。然后实现函数featureNormalize:用于标准化特征。
归一化:所有数据集应该都用训练集的均值和样本标准差处理(这里是样本标准差而不是总体标准差,使用np.std()时,ddof=1是样本标准差,默认ddof=0是总体标准差,而pandas默认计算样本标准差。),所以要将训练集的均值和样本标准差存储起来,对后面的数据进行处理。
def get_means_std(X):
mean=np.mean(X,axis=0)#求出每一个幂次i下 X^i的均值和标准差
std=np.std(X,axis=0,ddof=1)#ddof=1 means 样本标准差
return mean,std
def featureNormalize(example_X,example_mean, example_std):
example_X[:,1:]=example_X[:,1:]-example_mean[1:]
example_X[:,1:]=example_X[:,1:]/example_std[1:]
return example_X
设定扩展到X的 6 6 6次方:
power=6
获取添加多项式特征以及标准化之后的数据:
train_means,train_stds=get_means_std(X_poly_features(X,power).values)
X_norm=featureNormalize(X_poly_features(X,power).values, train_means, train_stds)
Xval_norm=featureNormalize(X_poly_features(Xval,power).values, train_means, train_stds)
Xtest_norm=featureNormalize(X_poly_features(Xtest,power).values, train_means, train_stds)
X_norm
array([[ 1.00000000e+00, -3.62140776e-01, -7.55086688e-01,
1.82225876e-01, -7.06189908e-01, 3.06617917e-01,
-5.90877673e-01],
[ 1.00000000e+00, -8.03204845e-01, 1.25825266e-03,
-2.47936991e-01, -3.27023420e-01, 9.33963187e-02,
-4.35817606e-01],
[ 1.00000000e+00, 1.37746700e+00, 5.84826715e-01,
1.24976856e+00, 2.45311974e-01, 9.78359696e-01,
-1.21556976e-02],
[ 1.00000000e+00, 1.42093988e+00, 7.06646754e-01,
1.35984559e+00, 3.95534038e-01, 1.10616178e+00,
1.25637135e-01],
[ 1.00000000e+00, -1.43414853e+00, 1.85399982e+00,
-2.03716308e+00, 2.33143133e+00, -2.41153626e+00,
2.60221195e+00],
[ 1.00000000e+00, -1.28687086e-01, -9.75968776e-01,
2.51385075e-01, -7.39686869e-01, 3.16952928e-01,
-5.94996630e-01],
[ 1.00000000e+00, 6.80581552e-01, -7.80028951e-01,
3.40655738e-01, -7.11721115e-01, 3.26509131e-01,
-5.91790179e-01],
[ 1.00000000e+00, -9.88534310e-01, 4.51358004e-01,
-6.01281871e-01, 9.29171228e-02, -2.18472948e-01,
-1.41608474e-01],
[ 1.00000000e+00, 2.16075753e-01, -1.07499276e+00,
2.66275156e-01, -7.43369047e-01, 3.17561391e-01,
-5.95129245e-01],
[ 1.00000000e+00, -1.31150068e+00, 1.42280595e+00,
-1.54812094e+00, 1.49339625e+00, -1.51590767e+00,
1.38865478e+00],
[ 1.00000000e+00, 4.03776736e-01, -1.01501039e+00,
2.73378511e-01, -7.41976547e-01, 3.17741982e-01,
-5.95098361e-01],
[ 1.00000000e+00, 9.29375305e-01, -4.19807932e-01,
5.10968368e-01, -5.88623813e-01, 3.82615735e-01,
-5.59030004e-01]])
def plot_fit(means,stds,l):
theta=TrainLinearReg(X_norm, y, l)
x=np.linspace(-75,55,50)
x=x.reshape(-1,1)
x=np.insert(x,0,1,axis=1)
x=X_poly_features(x,power)
x_norm=featureNormalize(x.values, train_means, train_stds)
PlotData(X, y)
plt.plot(np.linspace(-75,55,50),x_norm@theta,'b--')
plt.show()
学习的得到了参数 θ \theta θ后,使用 λ = 0 \lambda=0 λ=0,为多项式回归生成的两个图,如下图:
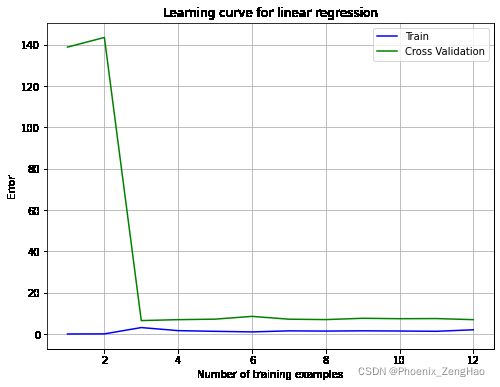
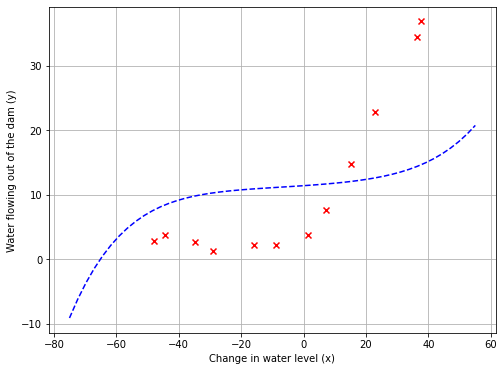
plot_fit(train_means, train_stds, 0)
plot_learning_curve(X_norm, y, Xval_norm, yval, 0)
从第一个图中,多项式拟合能够很好地拟合每一个数据点,所以获得了一个较低的训练误差。然而,多项式拟合是非常复杂的,甚至在极端值下降,这表明多项式回归模型训练时过拟合,不能很好地泛化。第二个图中,学习曲线显示了相同的效果:训练误差低,但交叉验证误差高,这样就更好地理解非正则化 λ = 0 \lambda=0 λ=0模型的问题。训练误差和交叉验证误差之间存在较大的差距,表明存在高方差问题(过拟合)。
解决高方差(过拟合)问题的一种方法是在模型中添加正则化。在下一节实验中,将尝试不同的 λ \lambda λ参数,来了解正则化如何得到更好的模型。
3.2 Optional (ungraded) exercise: Adjusting the regularization parameter(调整正则化参数)
在本节实验中,将观察正则化参数 λ \lambda λ如何影响正则化多项式回归的偏差-方差。继续使用之前的拟合模型,只需要修改 λ \lambda λ的参数( 1 , 100 1,100 1,100),对于每种参数 λ \lambda λ,生成对数据多项式的拟合和学习曲线图形。
对于 λ \lambda λ,可以看到一个很好地拟合数据的多项式拟合和一个学习曲线,这表明交叉验证误差和训练误差都收敛到一个相对较低的值。这表明 λ = 1 \lambda=1 λ=1时,正则化多项式回归模型不存在高偏差或高方差问题。实际上,它在偏差和方差之间实现了一个很好的权衡。
plot_fit(train_means, train_stds, 1)
plot_learning_curve(X_norm, y, Xval_norm, yval, 1)
对于 λ = 100 \lambda=100 λ=100,会看到一个不能很好地拟合数据的多项式拟合。在这种情况下,存在太多的正则化,模型无法拟合训练数据,即惩罚过多,导致了欠拟合。
plot_fit(train_means, train_stds, 100)
plot_learning_curve(X_norm, y, Xval_norm, yval, 100)
3.3 Selecting λ \lambda λ using a cross validation set(使用交叉验证集选择 λ \lambda λ)
从上一节实验中,可以观察到 λ \lambda λ的值可以显著地影响训练集和交叉验证集上的正则化多项式回归的结果。尤其是没有正则化的模型( λ = 0 \lambda=0 λ=0)可以很好地拟合训练数据,但不能泛化;而正则化模型( λ = 100 \lambda=100 λ=100)不能很好地拟合训练集和测试集。而 λ = 1 \lambda=1 λ=1可以提供一个很好的数据拟合。
在本节实验中,将实现一个方法来自动地选择 λ \lambda λ参数。具体来讲,将使用一个交叉验证集来评估每个 λ \lambda λ值的好坏。在使用交叉验证集选择最佳 λ \lambda λ值后,可以在测试集上评估模型,从而可以估计该模型在此数据集上的表现。在函数TrainLinearReg中使用不同的 λ \lambda λ的值来训练模型,并计算训练误差和交叉验证误差。 λ \lambda λ的范围集合: { 0 , 0.001 , 0.003 , 0.01 , 0.03 , 0.1 , 0.3 , 1 , 3 , 10 } \lbrace 0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10 \rbrace {0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10}
lambdas = [0., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1., 3., 10.]
errors_train, errors_val = [], []
for l in lambdas:
theta=TrainLinearReg(X_norm, y, l)
errors_train.append(CostReg(theta, X_norm, y,0))
errors_val.append(CostReg(theta, Xval_norm, yval,0))
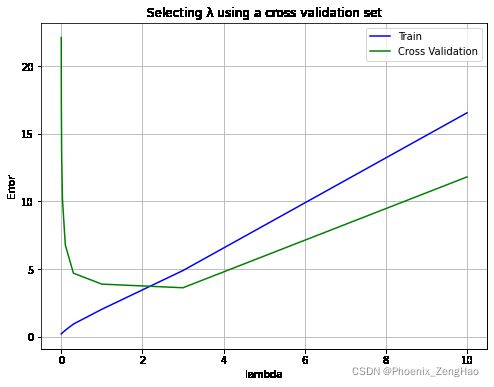
完成上述代码之后,会看到下方的图。在这个图中,可以看到 λ \lambda λ的最佳值大约等于 3 3 3。由于数据集的训练和验证分割的随机性,交叉验证误差有时会低于训练误差。
plt.figure(figsize=(8,6))
plt.plot(lambdas,errors_train,label="Train",color="blue")
plt.plot(lambdas,errors_val,label="Cross Validation",color="green")
plt.legend()
plt.xlabel('lambda')
plt.ylabel('Error')
plt.title('Selecting λ using a cross validation set')
plt.grid(True)
plt.show()
lambdas[np.argmin(errors_val)] # 交叉验证代价最小的是 lambda = 3
3.0
在下节实验中选择本实验中得到的最好的 λ \lambda λ参数。
3.4 Optional (ungraded) exercise: Computing test set error(计算测试集误差)
为了更好地显示模型在现实世界中的表现,在训练中没有使用过的测试集上评估"最终"模型是很重要的,因为它既不是用来选择 λ \lambda λ参数,也不是用来学习模型参数 θ \theta θ。在本节实验中,使用得到的最佳 λ \lambda λ值计算测试误差。在交叉验证中,得到了 λ = 3 \lambda=3 λ=3,并且测试误差大约为 3.8599 3.8599 3.8599。
theta=TrainLinearReg(X_norm,y,3)
print("l={}时,测试误差={}".format(3,CostReg(theta, Xtest_norm, ytest,0)))
l=3时,测试误差=4.75527177664976
看起来答案不太对,这是因为我在上面让 p o w e r = 6 power=6 power=6,这样绘制出来的图像才和pdf中的一样。那么接下来令 p o w e r = 8 power=8 power=8,重复上面的代码:
power=8
train_means,train_stds=get_means_std(X_poly_features(X,power).values)
X_norm=featureNormalize(X_poly_features(X,power).values, train_means, train_stds)
Xval_norm=featureNormalize(X_poly_features(Xval,power).values, train_means, train_stds)
Xtest_norm=featureNormalize(X_poly_features(Xtest,power).values, train_means, train_stds)
theta=TrainLinearReg(X_norm,y,3)
print("l={}时,测试误差={}".format(3,CostReg(theta, Xtest_norm, ytest,0)))
l=3时,测试误差=3.8599103904075482