机器学习 —— 支持向量机简单入门

第1关：线性可分支持向量机

1.线性二分类问题

经过前面的学习，我相信大家对线性二分类问题应该非常熟悉了，其本质上就是找到一条决策边界，将我们的数据分成两类。如下图：

图中的绿线与黄线都能很好的将图中的红点与蓝点给区分开。但是，哪条线的泛化性更好呢？可能你不太了解泛化性，也就是说，我们的这条直线，不仅需要在训练集（已知的数据） 上能够很好的将红点跟蓝点区分开来，还要在测试集（未知的数据） 上将红点跟蓝点给区分开来。

假如经过训练，我们得到了黄色的这条决策边界用来区分我们的数据，这个时候又来了一个数据，即黑色的点，那么你觉得黑色的点是属于红的这一类，还是蓝色的这一类呢？

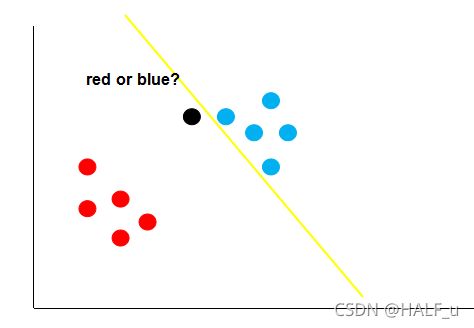
如上图，根据黄线的划分标准，黑色的点应该属于红色这一类。可是，我们肉眼很容易发现，黑点离蓝色的点更近，它应该是属于蓝色的点。这就说明，黄色的这条直线它的泛化性并不好，它对于未知的数据并不能很好的进行分类。那么，如何得到一条泛化性好的直线呢？这个就是支持向量机考虑的问题。

2.基本思想

支持向量机的思想认为，一条决策边界它如果要有很好的泛化性，它需要满足一下以下两个条件：

• 能够很好的将样本划分
• 离最近的样本点最远
  比如下图中的黑线
  
  它能够正确的将红点跟蓝点区分开来，而且，它还保证了对未知样本的容错率，因为它离最近的红点跟蓝点都很远，这个时候，再来一个数据，就不会出现之前黄色决策边界的错误了。
  
  无论新的数据出现在哪个位置，黑色的决策边界都能够很好的给它进行分类，这个就是支持向量机的基本思想。

3.间隔与支持向量

在样本空间中，决策边界可以通过如下线性方程来描述：

其中w=(w_1 ,w_2 ,…,w_d )为法向量，决定了决策边界的方向。b 为位移项，决定了决策边界与原点之间的距离。显然，决策边界可被法向量和位移确定，我们将其表示为 (w,b) 。样本空间中的任意一个点 x ,到决策边界 (w,b) 的距离可写为：

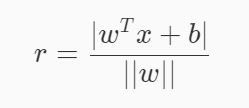
假设决策边界 (w,b) 能够将训练样本正确分类，即对于任何一个样本点 (x_i ,y_i ) ,若它为正类，即y_i =+1时，w^ T x+b ≥ +1。若它为负类，即y_i =−1时，w^ T x+b≤−1。

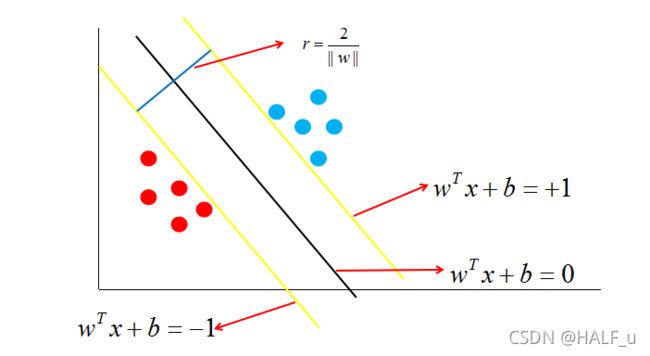
如图中，距离最近的几个点使两个不等式的等号成立，它们就被称为支持向量，即图中两条黄色的线。两个异类支持向量到超平面的距离之和为：

它被称为间隔，即蓝线的长度。欲找到具有 “最大间隔” 的决策边界，即黑色的线，也就是要找到能够同时满足如下式子的 w 与 b :

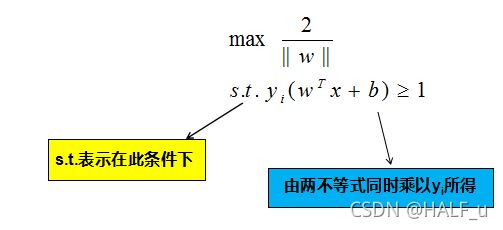
4.对偶问题

待补充。

5.选择题

1、按照支持向量机的思想，下图哪条决策边界的泛化性最好？

A、绿线
B、黑线
C、黄线

2、假设支持向量分别为
3x_1 +4x_2 +5=+1
3x_1 +4x_2 +5=−1
如下图：
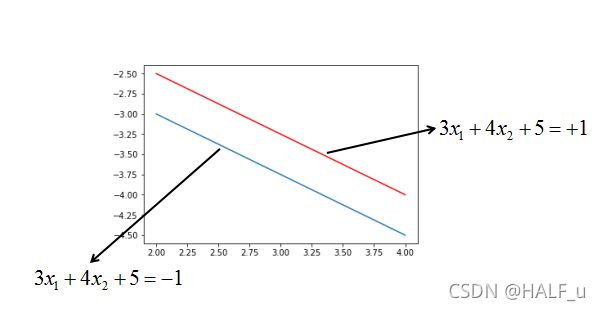则最大间隔r的值为？

A、0.3
B、0.4
C、0.5
D、2

3、假设有两个样本点：(V,+1),(-V,-1)。其中，V=(3,2)，则使得间隔最大的决策边界为：
(ps:x为横坐标轴，y为纵坐标轴)

A、x=0
B、y=0
C、3x+2y=0
D、2x+3y=0

4、有三个样本点：(x,+1),(y,+1),(z,-1)，超平面为:a+b=1。其中,x=(3,0),y=(0,4),z=(0,0),则以下说法错误的为：

A、超平面能够将三个样本点按类别分隔开来
B、样本y到超平面的距离为3
C、样本z到超平面的距离的平方为0.5
D、离超平面距离最近的样本为z

5、图中，最大间隔决策边界为：

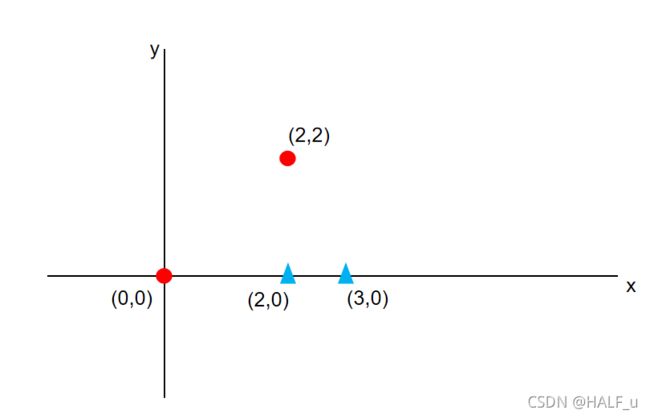
A、x+y+1=0
B、x-y+1=0
C、-x-y+1=0
D、-x+y+1=0

6、下面说法正确的是？

A、支持向量机的最终模型仅仅与支持向量有关。
B、支持向量机的最终模型由所有的训练样本共同决定。
C、支持向量机的最终模型由离决策边界最近的几个点决定。
D、训练集越大，支持向量机的模型就一定越准确。

第2关：线性支持向量机

本关任务：使用sklearn实现线性支持向量机，并通过癌细胞数据中训练集对模型进行训练，再对测试集癌细胞数据进行识别。

0.数据集介绍

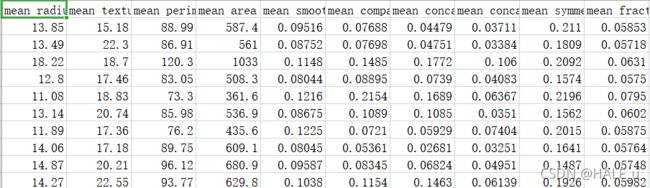
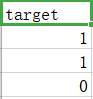
乳腺癌数据集，其实例数量是 569 ，实例中包括诊断类和属性，帮助预测的属性一共 30 个，各属性包括为 radius 半径（从中心到边缘上点的距离的平均值），texture 纹理（灰度值的标准偏差）等等，类包括：WDBC-Malignant 恶性和 WDBC-Benign 良性。用数据集的 80% 作为训练集，数据集的 20% 作为测试集，训练集和测试集中都包括特征和诊断类。

想要使用该数据集可以使用如下代码：

import pandas as pd
# 获取训练数据
train_data = pd.read_csv('./step1/train_data.csv')
# 获取训练标签
train_label = pd.read_csv('./step1/train_label.csv')
train_label = train_label['target']
# 获取测试数据
test_data = pd.read_csv('./step1/test_data.csv')

数据集中部分数据与标签如下图所示：

1.软间隔

假如现在有一份数据分布如下图：

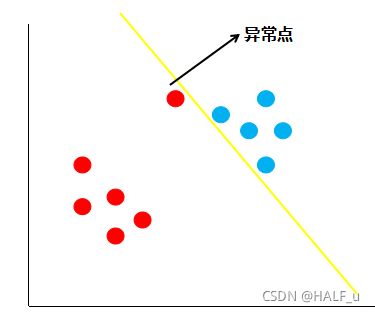
按照线性可分支持向量机的思想，黄色的线就是最佳的决策边界。很明显，这条线的泛化性不是很好，造成这样结果的原因就是数据中存在着异常点，那么如何解决这个问题呢，支持向量机引入了软间隔最大化的方法来解决。

所谓的软间隔，是相对于硬间隔说的，即之前我们所讲的支持向量机学习方法。回顾下硬间隔最大化的条件：

接着我们再看如何可以软间隔最大化呢？SVM 对训练集里面的每个样本(x_i ,y_i )引入了一个松弛变量x_i ≥0,使函数间隔加上松弛变量大于等于 1 ，也就是说：

对比硬间隔最大化，可以看到我们对样本到超平面的函数距离的要求放松了，之前是一定要大于等于 1，现在只需要加上一个大于等于 0 的松弛变量能大于等于 1 就可以了。也就是允许支持向量机在一些样本上出错，如下图：

2.LinearSVC

官方文档
中文翻译

2.1 LinearSVC与SVC的区别

LinearSVC

• 基于liblinear库实现
• 有多种惩罚参数和损失函数可供选择
• 训练集实例数量大（大于1万）时也可以很好地进行归一化
• 既支持稠密输入矩阵也支持稀疏输入矩阵
• 多分类问题采用one-vs-rest方法实现

SVC

• 基于libsvm库实现
• 训练时间复杂度为 [公式]
• 训练集实例数量大（大于1万）时很难进行归一化
• 多分类问题采用one-vs-rest方法实现

2.2 详细说明

LinearSVC实现了线性分类支持向量机，它是给根据liblinear实现的，可以用于二类分类，也可以用于多类分类。
其原型为：

class Sklearn.svm.LinearSVC(
	penalty=’l2’, 
	loss=’squared_hinge’, 
	dual=True, 
	tol=0.0001, 
	C=1.0, 
	multi_class=’ovr’, 
	fit_intercept=True, 
	intercept_scaling=1, 
	class_weight=None, 
	verbose=0, 
	random_state=None, 
	max_iter=1000)

2.3 初始化参数

• C：一个浮点数，惩罚参数
• loss：字符串。表示损失函数。
  • 可取值为 ‘hinge’：合页损失函数；
  • ‘squared_hinge’：合页损失函数的平方
• penalty：字符串。可取值为’l1’和’l2’分别对应1范数和2范数
• dual：布尔值。
  • 如果为true，则求解对偶问题。
  • 如果为false，解决原始问题。当样本数量>特征数量时，倾向采用解原始问题
• tol：浮点数，指定终止迭代的阈值
• multi_class: 字符串，指定多分类问题的策略
  • ‘ovr’: 采用one-vs-rest分类策略；
  • ‘crammer_singer’: 多类联合分类，很少用。因为它的计算量大，而且精度不会更佳，此时忽略loss,penalty,dual参数
• fit_intercept:布尔值。如果为true，则计算截距，即决策函数中的常数项；否则忽略截距
• intercept_scaling:浮点值。如果提供了，则实例X变成向量[X,intercept_scaling]。此时相当于添加了一个人工特征，该特征对所有实例都是常数值
• class_weight: 可以是个字典，或者字符串’balanced’。指定各个类的权重，若未提供，则认为类的权重为1
  • 如果是字典，则指定每个类标签的权重；
  • 如果是’balanced’，则每个类的权重是它出现频率的倒数
• verbose:一个整数，表示是否开启verbose输出。启用详细输出。 请注意，此设置利用liblinear中的每进程运行时设置，如果启用，可能无法在多线程上下文中正常工作。
• random_state: 一个整数或者一个RandomState实例，或者None
  • 如果为整数，则它指定随机数生成器的种子
  • 如果为RandomState实例，则指定随机数生成器 如果为None，则使用默认的随机数生成器
• max_iter:一个整数，指定最大的迭代次数

2.4 属性

coef_: 一个数组，它给出了各个特征的权重
intercept_:一个数组，它给出了截距，即决策函数中的常数项

2.5 方法

fix(X,y): 训练模型
predict(X): 用模型进行预测，返回预测值
score(X,y[, sample_weight]):返回在(X, y)上预测的准确率

3.代码示例

#encoding=utf8
from sklearn.svm import LinearSVC
import pandas as pd

def linearsvc_predict(train_data,train_label,test_data):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********# 
    # 获取训练数据
    train_data = pd.read_csv('./step1/train_data.csv')
    # 获取训练标签
    train_label = pd.read_csv('./step1/train_label.csv')
    train_label = train_label['target']
    # 获取测试数据
    test_data = pd.read_csv('./step1/test_data.csv')

    cls = LinearSVC(C = 0.99,max_iter=2000,dual=False,tol=1e-5)
    cls.fit(train_data, train_label)
    predict = cls.predict(test_data)
    #********* End *********# 
    return predict

—— 实际输出 ——
正确率大于0.95