粒子群(PSO)算法（附完整Matlab代码，可直接复制）

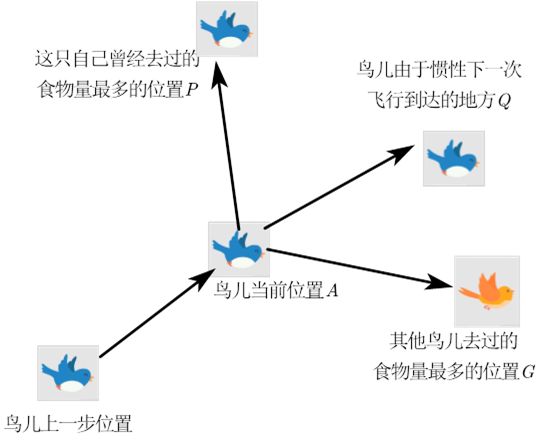
在粒子群优化算法中，每个解可用一只鸟（粒子）表示，目标函数就是鸟群所需要寻找的食物源。寻找最优解的过程中，粒子包含两种行为：个体行为和群体行为。

个体行为：粒子根据自身在寻优过程中的最优解更新自己的位置。

群体行为：粒子根据群体在寻优过程中的最优解更新自己的位置。

假设N个粒子组成1个粒子群，每个粒子都是一个D维向量，则每个粒子的位置为：

 将其代入适应度函数计算出适应度值，第i个粒子经历过的最优适应度值的位置记为个体历史最优：

整个粒子群经历过的最优位置记为全局最优：

第i个粒子的飞行速度记为：

则第t+1轮迭代后第i个粒子的第j维速度为：

位置更新为：

若粒子位置任何一维超出限定的上界ub和下界lb,则将其直接赋值为ub或lb。

粒子群PSO完整Matlab代码如下：

clc;
clear all;
close all;
pop=50;
dim=2;
ub=[10,10];
lb=[-10,-10];
vmax=[2,2];
vmin=[-2,-2];
maxIter=100;
fobj=@(X)fun(X);
[Best_Pos,Best_fitness,IterCurve]=pso(pop,dim,ub,lb,fobj,vmax,vmin,maxIter);
figure
plot(IterCurve,'r','linewidth',2);
grid on;
disp(['求解得到的x1，x2是:',num2str(Best_Pos(1)),' ',num2str(Best_Pos(2))]);
disp(['最优解对应的函数:',num2str(Best_fitness)]);


%pop——种群数量
%定义粒子群种群初始化函数


function [X]=initialization(pop,ub,lb,dim)
    for i=1:pop
        for j=1:dim
            X(i,j)=(ub(j)-lb(j))*rand()+lb(j);%在限定的  
        end 
    end
end

function fitness=fun(x)
    fitness=sum(x.^2);
end

function [X]=BoundaryCheck(X,ub,lb,dim)
    for i=1:dim
        if X(i)>ub(i)
            X(i)=ub(i);
        end
        if X(i)

 相关阅读：

1、粒子群（PSO）优化算法（附完整Matlab代码，可直接复制）

2、灰狼（GWO）优化算法（附完整Matlab代码，可直接复制）

3、正余弦（SCA）优化算法（附完整Matlab代码，可直接复制）

4、萤火虫（FA）优化算法（附完整Matlab代码，可直接复制）

5、果蝇（FOA）优化算法(附完整Matlab代码，可直接复制）