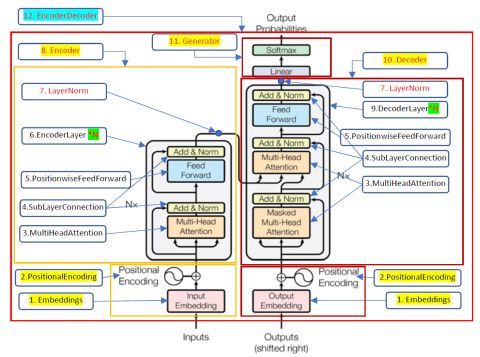
（无敌详细+链接代码注释版）深度学习-图解Transformer (变形金刚)
原文链接：https://zhuanlan.zhihu.com/p/105493618
快速导航：
英文原文来自：杰伊·阿拉玛（Jay Alammar）: 一次对机器学习的一个概念进行可视化分析
本文对其进行了中文翻译和一定的纠错(error-fix)和扩展(new)。
图解 Transformer (变形器、变形金刚)
Original version author: Jay Alammar, translated and updated by Xianchao Wu
Who am I? https://sites.google.com/site/xianchaowu2012/
英文原版：http://jalammar.github.io/illustrated-transformer/
(麻省理工学院的深度学习最新技术讲座引用了这篇文章的英文版)
在上一篇文章中，我们研究了注意力模型(attention models) -现代深度学习模型中无处不在的方法。Attention是帮助提高神经机器翻译(Neural Machine Translation)应用程序性能的重要概念。在本文中，我们将介绍Transformer，该模型使用Self-Attention机制，其摈弃了传统的RNN(例如GRU, LSTM)网络的序列化计算的限制（即：t时间的隐状态的计算，依赖于t-1时间的隐状态，或者t+1时间的隐状态），可以通过高速并行矩阵运算来加快训练和解码的速度。在特定任务中，Transformer优于Google神经机器翻译模型(基于RNN+attention机制的版本)。
除了卓越的精度(BLEU)表现，Transformer的最大的好处来自于其适合并行化。实际上，Google Cloud的建议是使用Transformer作为参考模型来使用其Cloud TPU产品。因此，让我们尝试将模型分开，看看它是如何工作的。
论文
开篇几个问题(new)，如果您都能回答的很好，请忽略此文：
1. Multi-head attention中有哪些可训练参数？
2. 一个输入batch都有什么变量，分别是什么数据结构？分别是如何得到的？
3. 输入序列需要mask吗？为什么？
4. 位置编码的 具体的 例子？例如，一个句子的第一个词的位置编码是什么？
5. 看transformer的架构图的前提下，说出每个模块的可训练参数都有哪些，分别是什么数据结构(shape of the tensors – trainable parameters)？
概览
让我们从将模型视为一个黑匣子black-box开始。在一个机器翻译应用程序中，它将采用一种语言的句子，然后以另一种语言输出其翻译。
图1，Transformer整体框架示例。
图1，Transformer整体框架示例。例子：输入是一句法语，Je=I/我；suis=am/是；etudiant=student/学生。输出是一个英文句子，I am a student。
类似于变形金刚(Transfomer电影)中的擎天柱，我们看到了Encoder编码组件（车头），Decoder解码组件（车尾）以及它们之间的Transformer连接（车身）。（或者说，汽油/input energy，运动/output energy，发动机/engine）
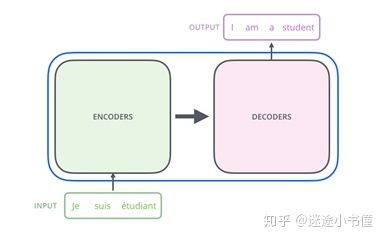
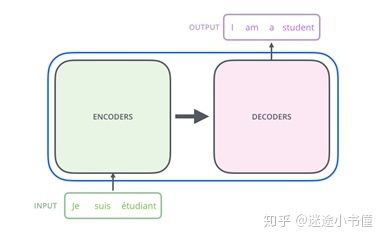图2，包含两个部分, encoders编码器和decoders解码器的Transformer。
Encoder编码组件是一堆编码器（或者，编码层Encoder Layers，论文上将六个编码器彼此叠放–数字6没有什么神奇之处，我们也可以尝试其他设置，例如N=18, 4等等）。解码组件是一堆相同数量的解码器。虽然解码器名字为解码，其内部也包括了，对于已经翻译好的部分句子（例如翻译到I am a的时候）的编码表示，以及参考encoder的源语言句子的表示矩阵(memory)的注意力机制和解码softmax选词。
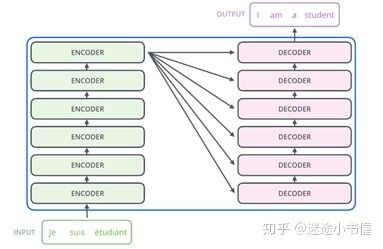
图3，包括六层encoder和六层decoder的Transformer的展开示意图。为了统一期间，Encoder从下到上，分别编号为#0, #1, …, #5。同样，Decoder从下到上，也是分别编号为#0, #1, …, #5。
编码器（六个编码层）的结构均相同（但它们不共享权重，也就是说，每一层的可训练参数都独立拥有数值，梯度和更新）。每一层都分为两个子层：
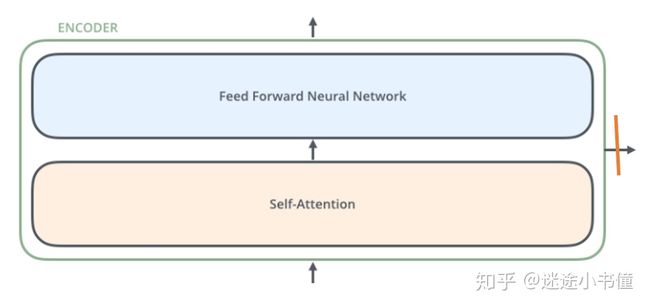
图4，一层encoder的内部构造，包括两个子层，self-attention/自注意力sublayer和前向反馈/feed forward神经网络sublayer。需要注意的是，右边的箭头，不一定有！
一层编码器的输入首先流经自注意力层self-attention sublayer，该层可以帮助编码器在对特定单词进行编码时查看输入句子中的其他单词。我们将在后面的文章中进一步关注self-attention机制的细节。
自我注意层self-attention sublayer的输出被馈送到前馈神经网络feed-forward sublayer。完全相同的前馈网络独立应用于一个输入句子的每个位置上的单词，所以又称为point-wise feed-forward neural network (这里的Point=word)。
解码器Decoder也具有这两层(self-attention sublayer + feed forward sublayer)，但是在它们之间是一个注意力层，可以帮助解码器将注意力集中在输入语句的相关部分（即：某些词上，例如翻译出I的时候, Je的贡献最大）上（类似于seq2seq模型中的attention机制）。
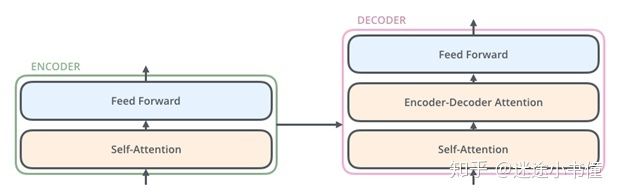
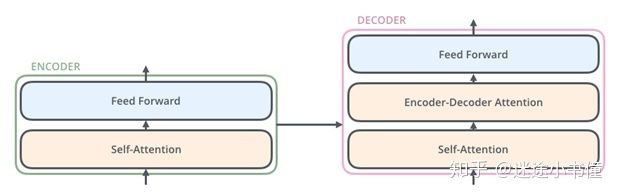
图5，更加精细的encoder层（两个子层sublayers）和decoder层（三个子层sublayers）。其中encoder-decoder attention sublayer是连接了encoder和decoder。
把张量画出来
现在，我们已经看到了模型的主要组件，让我们开始研究各种矢量/张量以及它们在这些组件之间的流动方式，以将经过训练的模型的输入转换为输出。
通常，在NLP应用程序中，我们首先使用嵌入算法(Embedding algorithm)将每个输入词转换为向量。
图6，词向量嵌入表示的示例。例如，每个单词都嵌入大小为512的向量中。我们将用这些简单的框表示这些向量。本图中，我们使用了4维向量来表示一个单词。从而，输入的三个单词，分别用x1, x2, 和x3表示出来了。
嵌入(Embedding)仅发生在最底层的编码器中。所有编码器共有的抽象概念是，它们接收一个向量列表，每个向量的大小均为512（例如，论文中使用的512维） –在底部编码器中是单词嵌入，但在其他层编码器中，它将是直接在其下面一层的编码器的输出。该向量列表的大小是我们可以设置的超参数–基本上，这就是训练数据集中最长句子的长度。
特别地，如果一个句子有3个词，每个词被表示为一个四维向量（本文使用的例子），则输入的向量列表，其实是一个3行4列的矩阵。这里的3就是所谓“向量列表”的大小。因为实际有多个双语言对，每一对句子的长度和其他对不一定一样，所以我们可以分别取source sentence的最长的长度，以及target sentence的最长的长度。如果一个句子不足该长度，则在右边补0.（padding）
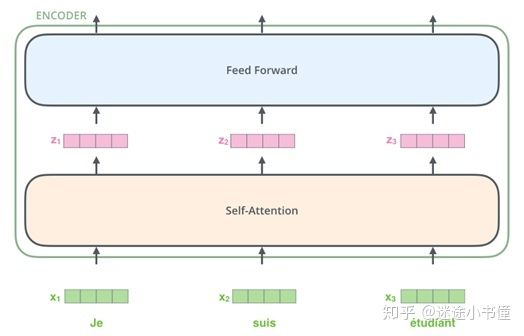
图7，综合各个词的向量表示来计算的self-attention sublayer和相对独立计算的feed forward层。
我们的输入序列中的单词完成嵌入表示之后，它们中的每一个都会流经编码器的两层(two sublayers)。
在这里，我们开始看到Transformer的一个关键属性，即每个位置的单词都流经编码器中自己的路径。自我注意层(self-attention sublayer)中这些路径之间存在依赖性。但是，前馈层(feed-forward sublayer)不具有这些依赖性，因此可以在流过前馈层的同时并行执行各种路径。
接下来，我们将示例切换到较短的句子，然后看一下编码器每个子层(sublayer)中发生的情况。
现在我们开始编码！
正如我们已经提到的，编码器接收向量列表（即，2行4列的一个矩阵,2个单词）作为输入。它通过将这些向量传递到“自注意力”层(self-attention sublayer)，然后传递到前馈神经网络，然后将输出向上发送到下一层编码器来处理此列表。
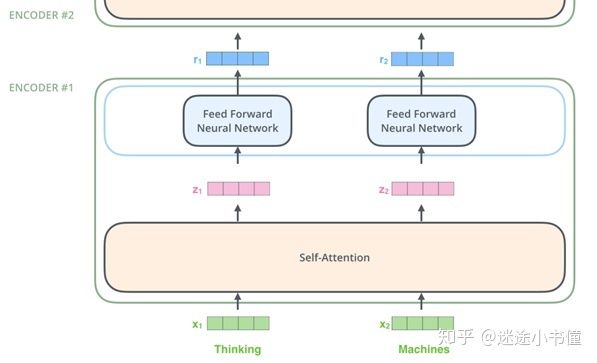
图8，交叉计算的self-attention sublayer和独立计算的feed forward sublayer的示例。这里假设我们的输入有两个单词，Thinking和Machines。每个单词用一个四维向量表示。每个位置的单词都经过一个自我注意过程(self-attention process)，得到两个向量z1和z2。然后，它们（z1和z2）每个都通过前馈神经网络-(完全相同的网络)，每个向量独立地流过feed-forward sublayer，得到两个新的向量r1和r2。
如前所述，这里的一个关键点在于，计算z1和z2的时候，使用的self-attention sublayer会综合考虑x1和x2（也就是x1, x2的两条计算路径会有交叉，交叉方法后述: multi-head dot-product attention） 。但是在计算r1和r2两个向量的时候，z1和z2之间不会进一步相互影响，而是分别独立地流过feed-forward sublayer。需要注意的是，图里面的ENCODER #1 应该是ENCODER #0，以此类推。
概括一下自注意力self-attention
不要被 “自注意力”(self-attention)一词所迷惑，因为这是每位学习深度学习的人都应该熟悉的概念。在阅读《注意力就是您需要的一切-Attention is All You Need》论文之前，我个人从未遇到过这个概念。让我们提炼一下它是如何工作的。
假设下面的句子是我们要翻译的输入句子：
” The animal didn't cross the street because it was too tired“
这句话中的“它”(it)指的是什么？是指街道street还是动物animal？对人类来说，这是一个简单的问题，但对算法而言却不那么简单。
当模型处理单词“ it”时，自注意力机制使它能够将“ it”与“ animal”相关联。
在模型处理每个单词（输入序列中的每个位置）时，自注意力使其能够查看输入序列中的其他位置以寻找线索，从而有助于更好地对该单词进行编码。这相当于参考了上下文信息context来对当前单词进行强化表示。类似的思想也反映在RNN, LSTM, GRU等神经网络中。
如果您熟悉RNN，请考虑一下如何通过保持隐藏状态(hidden states)来使RNN将其已处理的先前单词/向量的表示形式与正在处理的当前单词/向量进行合并。自注意力机制(self-attention mechanism，这里的self是站在一个句子的角度来看的，类似于sentence-level self-attention，考虑的是sentence里面word之间的隐含语义依赖关系)是Transformer用于将其他相关单词的“理解”烘焙（融合）到我们当前正在处理的单词的语义表示中的方法。
图9，自注意力机制的示例。当我们在编码器第5层（encoder堆栈中的顶部编码器层，ENCODER #5）中对单词“ it”进行编码时，注意力机制的一部分集中在“ The Animal”上，并将其表示(vector)的一部分(按照权重，也就是the和it的语义上的关联度，以及animal和it的语义上的关联度)烘焙（融合）到“ it”的编码表示中。 （该图中，颜色越深，代表和it的关联度越大）
确保您查看Tensor2Tensor的代码（https://colab.research.google.com/github/tensorflow/tensor2tensor/blob/master/tensor2tensor/notebooks/hello_t2t.ipynb），您可以在其中加载Transformer模型，并使用此交互式可视化文件对其进行检查和学习。
其实这个代码不容易读… 个人推荐：
1. http://nlp.seas.harvard.edu/2018/04/03/attention.html
2. https://github.com/jadore801120/attention-is-all-you-need-pytorch
自注意力机制的细节
首先，让我们看一下如何使用向量计算自注意力，然后着眼于它是如何实现的-使用矩阵。
在第一步骤中，计算自注意力的关键是从每个编码器的输入向量来创建三个向量（在encoder这种情况下，每个词的嵌入向量）。因此，对于每个单词，我们创建一个查询向量(query vector)，一个键向量(key vector)和一个值向量(value vector)。通过将词嵌入向量(word embedding vector)乘以我们在训练过程中训练的三个矩阵（参数，可训练），可以创建这些向量。
请注意，这些新向量的维数小于词嵌入向量的维数。在论文中，它们的维数为64，而嵌入和编码器输入/输出矢量的维数为512。它们不必较小，这是使多头注意力计算（大约）保持恒定的体系结构选择。
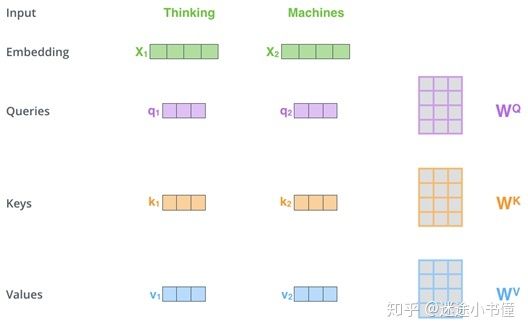
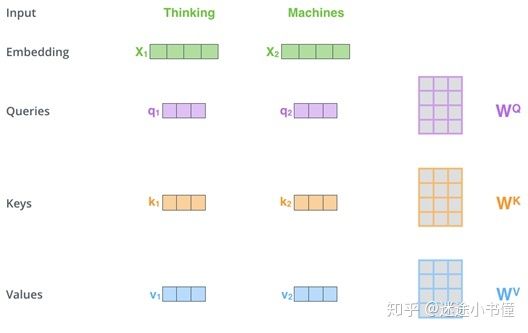
图10. 构建查询向量，键向量和值向量的示例。X1乘以WQ权重矩阵产生q1，即，与该词thinking相关联的“查询”向量。X1乘以WK权重矩阵产生k1，即，与该词thinking相关联的“键”向量。X1乘以WV权重矩阵产生v1，即，与该词thinking相关联的“值”向量。同理，对于词machines，我们可以复用WQ, WK, WV来得到q2, k2和v2。由此，我们最终为输入句子中的每个单词创建了一个“查询”，一个“键”和一个“值”投影。 由于WQ, WK, 和WV是分别初始化的，所以得到的三个向量(q1, k1, v1)不一定是相同的。
什么是“查询”，“键”和“值”向量？
它们是对计算和思考注意力有用的抽象。继续阅读下面的注意力计算方式后，您将几乎了解所有关于这些向量所起的作用。
在第二个步骤中计算自注意的是，计算得分。假设我们正在计算此示例中的第一个单词“ Thinking”的自注意力。我们需要对该单词和输入句子的每个单词的“语义关联度”进行评分。分数决定了当我们对某个位置的单词进行编码时，将注意力集中在输入句子的其他部分上的程度。（或者说，其他词对于当前词的影响力：哪些词对于当前词很重要，哪些词不重要。例如前面的it和the animal的关系就是非常重要的）
通过将“查询”向量与我们要打分的各个单词的“键”向量的点积相乘来计算关联度分数。因此，如果我们正在处理位置＃1上的单词的自注意力，则第一个分数将是q1和k1的点积。第二个分数是q1和k2的点积。
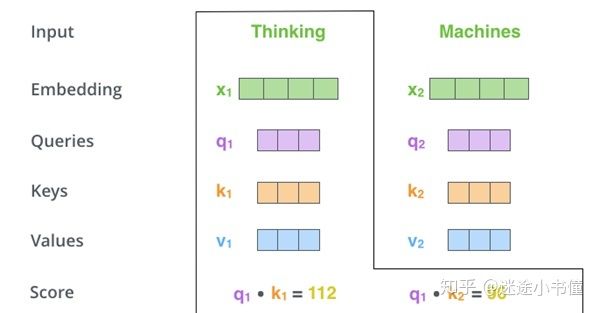
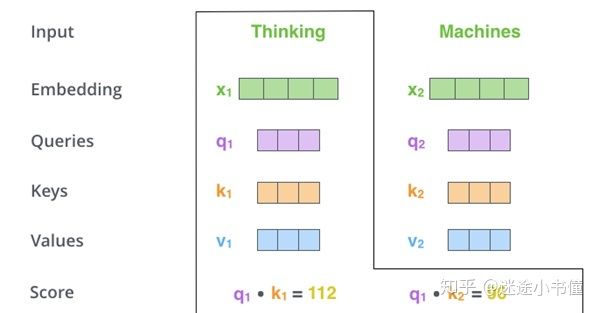
图11，点积（内积，点乘）q1和k1，k2得到Thinking和Thinking自己，Thinking和Machines的相关度得分。
第三和第四步骤是把上面的点积除以维度64的平方根8（在论文中使用的“键”向量的维数的平方根来划分的分数- 64。这导致具有更稳定的梯度。可以是其他可能的值，64是一个默认值），然后通过softmax操作传递结果。Softmax对分数进行归一化，因此所有分数均为正，加起来为1。
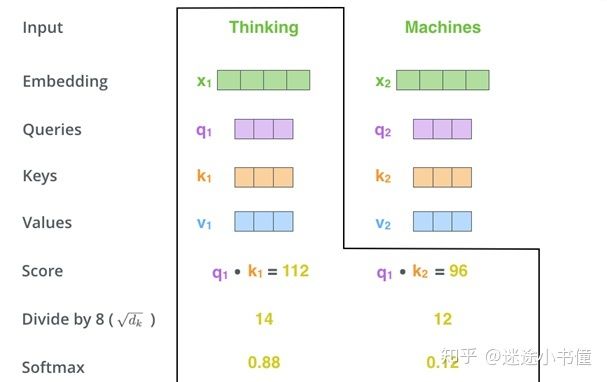
图12，使用sqrt(d_k)来防止过大的得分，并使用softmax来归一化到概率类型的权重向量上。
这个softmax分数(exp(14)/(exp(14)+exp(12))=0.88, exp(12)/(exp(14)+exp(12))=0.12)决定了每个单词在当前位置（例如，Thinking在句子”Thinking Machines”中所在的位置）要表达多少。显然，此位置的单词具有最高的softmax分数(0.88)，但是有时建立起来与当前单词相关的另一个单词的注意力很有用。
第五步骤是由SOFTMAX得分乘以每个“值”向量（value vector）。直觉是保持我们要关注的单词的值（向量表示）的完整性，并淹没无关的单词（例如，将它们乘以0.001之类的小数字）。
第六步骤是对加权值向量求和。这将在此位置（对于第一个单词）产生自注意力层的输出。类似于，z1=0.88*v1 + 0.12*v2.
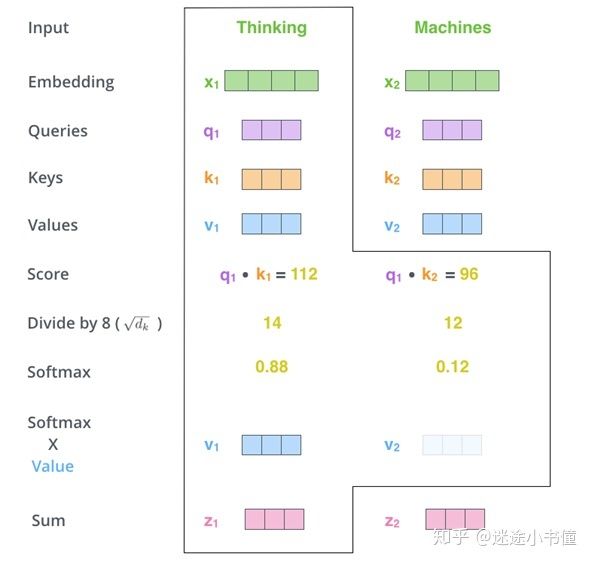
图13，对v1和v2按照0.88, 0.12加权求和，就得到了自注意力sublayer的对于Thinking的（参考了上下文的，encoder的部分，是上下文；decoder的部分，只有上文，没有下文）向量表示的构建。
这样就完成了自注意力的计算。生成的向量(z1和z2)是我们可以发送到前馈神经网络(feed-forward network)的向量。但是，在实际实现中，此计算以矩阵形式进行，以加快处理速度。现在，让我们来看一下单词级别上的直觉计算。
自注意力的矩阵计算
第一步是计算查询，键和值矩阵。为此，我们将句子的词嵌入向量打包到一个矩阵X中，然后将其乘以我们训练过的（或者随机初始化过的）权重矩阵（WQ，WK，WV）。
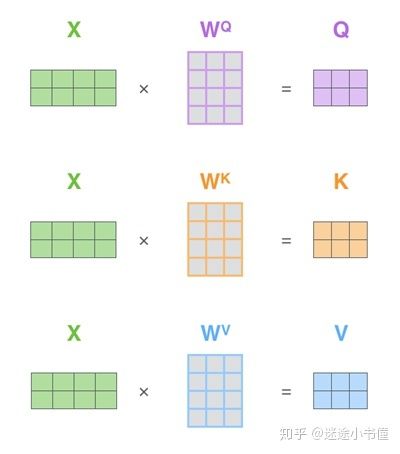
图14，句子单位的计算示例。X矩阵 中的每一行对应于输入句子中的一个单词。我们再次看到词嵌入向量X（图中的512或4个框）和q / k / v向量（图中的64或3个框）的大小差异。 X是两个词，每个词用一个四维向量表示，例如Thinking Machines。所以X是2行4列，这里定义三个权重矩阵WQ, WK, 和WV都是4行三列的，从而得到的三个矩阵，Q, K, V都是2行3列的。Q的第一行是q1，第二行是q2。
最后，由于我们要处理矩阵，因此我们可以将步骤2到6压缩成一个公式，以计算自我注意层的输出。
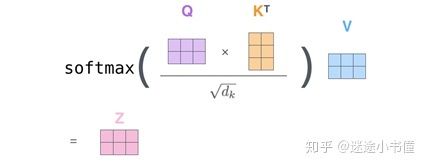
图15，矩阵形式的自注意力计算 。得到的Z矩阵是2行三列，第一行为z1，第二行为z2。
多头(multi-head)注意力“野兽”
论文中通过添加一种称为“多头”注意力的机制，进一步完善了自注意力层。这样可以通过两种方式提高注意力层的性能：
其一，它扩展了模型专注于不同位置的能力。是的，在上面的示例中，z1包含所有其他单词的编码向量的一点点，但是它可能由实际单词本身决定。如果我们要翻译这样的句子（例如“The animal didn’t cross the street because it was too tired/动物没过马路，因为它太累了。”），这很有用，我们想知道“它”指的是哪个单词。
其二，它为注意力层提供了多个“表示子空间”。正如我们接下来将要看到的，在多头注意力下，我们不仅拥有一个查询，而且具有多组查询/键/值权重矩阵（Transformer使用八个关注头，因此每个编码器/解码器最终得到八组） 。这些集合的每一个都是随机初始化的。然后，在训练之后，使用每个集合将输入的嵌入（或来自较低层编码器/解码器的向量）投影到不同的表示子空间中。
图16，双头注意力的计算示例。在多头注意力下，我们为每个头维护单独的Q / K / V权重矩阵，从而得到不同的Q / K / V矩阵。如前所述，我们将X乘以WQ / WK / WV矩阵以生成Q / K / V矩阵。此图展示了两个头的时候的例子，#0和#1，分别使用不同的WQ, WK,和WV矩阵。
如果我们执行上面概述的相同的自注意力计算，则在八个不同的次数上使用不同的权重矩阵，最终将得到八个不同的Z矩阵：
图17，八头(eight-heads)注意力的计算示例。
这给我们带来了一些挑战。前馈层(feed forward sublayer)不期望有八个矩阵-它期望一个矩阵（每个单词一个向量）。因此，我们需要一种将这八个矩阵合并为单个矩阵的方法。
我们该怎么做？我们合并矩阵，然后将它们乘以一个权重矩阵WO。
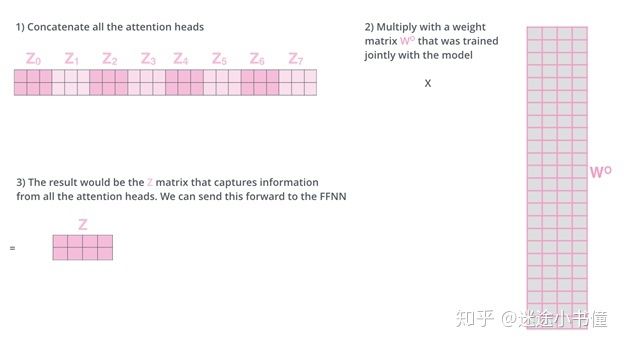
图18，自注意力层(self-attention sublayer)和前向反馈层(feed forward sublayer)的衔接计算。本图分三步，其一串联起来八个矩阵，本来是八个2*3的矩阵，现在得到的是一个2*24的矩阵。其二是让得到的2*24矩阵乘以一个权重矩阵WO(24行4列)，得到Z，是2行4列的一个最终矩阵，类似的，Z矩阵的第一行是对应Thinking的向量z1；第二行是对应Machines的向量z2。
这就是多头自我关注的全部内容。我知道这里出现了很多矩阵。让我尝试将它们全部放在一个图片中，以便我们可以在一处查看它们：
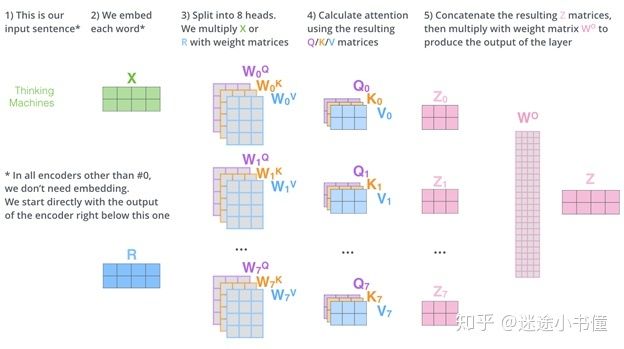
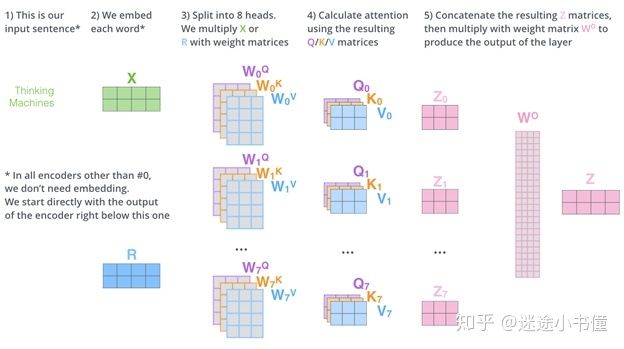
图19，综合示例一个encoder层，包括最初的输入句子，词嵌入矩阵，八头自注意力计算，前向反馈网络矩阵，以及最后的encoder单层输出。
小练习(new)，让我们数一下这里的可训练参数的个数：
1. 词嵌入矩阵，假设只有两个词，每个词是一个4维向量，则为2*4=8；
2. WQ0, WK0, WV0到WQ7, WK7, WV7，一共是24个矩阵，每个矩阵是4*3的；
3. WO是一个矩阵，是24*4的；
所以，该图中（在不考虑其他层，例如残差层等的前提下）的参数为：8+24*4*3+24*4=392。
既然我们已经涉及到注意头，那么让我们回顾一下示例，看看在示例句中对单词“ it”进行编码时，不同的注意头所关注的位置：
图20，以双头为例，谁和it相关？当我们对“ it”一词进行编码时，一个注意力头(attention head)集中在“动物”上（左边列的土黄色），而另一个attention head则集中在“累了”上（右边列的绿色）。从而it的向量表示，融合了“动物”和“累”这两个词的信息。 这里展示的仍然是Encoder的最高一层ENCODER #5的输出的示例。
但是，如果将所有注意力头attention-heads添加到图片中，则可能很难直观地解释：
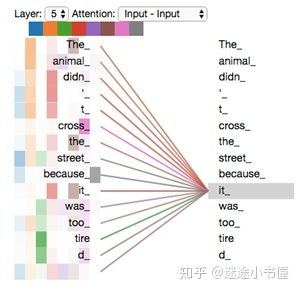
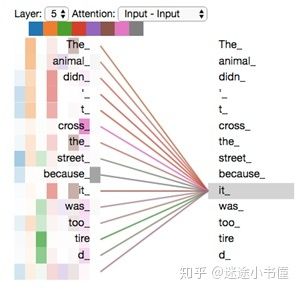
图21, 八头注意力机制下的it都和哪些词相关的示例。
当然，我们其实可以看一下这个句子的依存关系树(new)（http://nlp.stanford.edu:8080/corenlp/process ）：
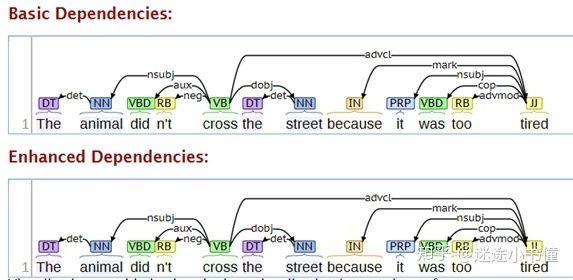
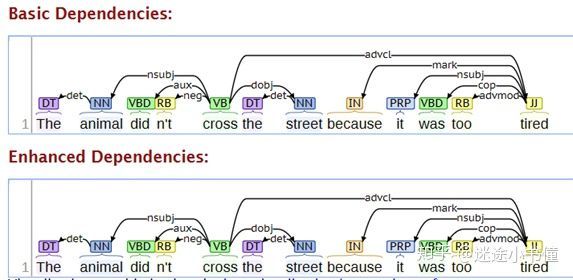
图22，英语例句的依存分析树。通过多头注意力机制，我们其实在潜在语义层面上，把it相关的所有单词，通过不同的依存路径（指向it的路径，父路径，以及更高层级的路径），表现在了其最终的向量表示上了。
使用位置编码表示序列的顺序
到目前为止，我们描述的模型中缺少的一件事是，一种解决输入序列中单词顺序的方法。
为了解决这个问题，Transformer将位置编码向量添加到每个输入的词嵌入中。这些向量遵循模型学习的特定模式，这有助于确定每个单词的位置或序列中不同单词之间的距离。直觉是，将这些值添加到嵌入中后，一旦将它们投影到Q / K / V向量中以及在点积注意期间，就可以在嵌入向量之间提供有意义的距离。当然，使用相对位置编码，可以在后续的论文Self-Attention with Relative Position Representations(https://arxiv.org/abs/1803.02155 )和Transformer-XL(https://arxiv.org/abs/1901.02860 )中找到细节。
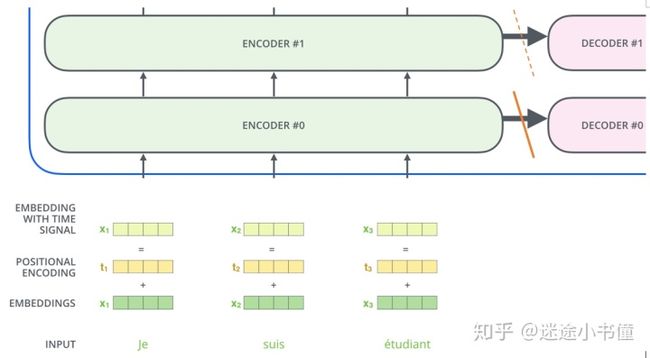
图23，引入位置编码。为了使模型具有单词的顺序感，我们添加了位置编码向量，并且，位置编码向量遵循特定的模式。需要注意的一点是，ENCODER #0 并没有箭头直接指向DECODER #0。ENCODER #1也并没有箭头直接指向DECODER #1。只有最高一层ENCODER #5会把source sentence打包编码好的结果矩阵，统一扔给DECODER的各层。(error-fix)
如果我们假设词嵌入的维数为4，则实际的位置编码应如下所示：
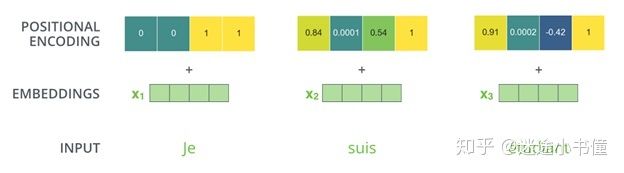
图24，（和论文不一致的, error-fix）位置编码的示例。
玩具toy词嵌入大小为4的位置编码的真实示例
注意：如果按照论文中的公式，这几个值其实是有问题的，实际的计算方法为：
PE(pos, 2i) = sin(pos/power(10000, 2i/d_model)) ---- （1）
PE(pos, 2i+1) = cos(pos/power(10000, 2i/d_model)) ---- (2)
这里，d_model=4；pos为位置，从0开始；i是编码向量的维度下标。
对于第0个位置Je，其位置编码向量的四个值为：
pos=0:
i=0, 则表示i=2*j, j=0, 因为i是偶数，要代入公式(1)，得到sin(0/power(10000, 0/4))=0;
i=1, 则表示i=2*j+1，2*j=0，因为i是奇数，要代入公式(2)，得到cos(0/power(10000, 0/4))=1;
i=2, 则表示i=2*j, j=1，代入公式(1)，得到sin(0/power(10000, 2/4))=0;
i=3, cos(0/power(10000, 2/4))=1;
所以Je的位置编码向量为（0, 1, 0, 1）。
pos=1:
i=0=2*j, j=0, sin(1/power(10000, 0/4))=sin(1)=0.8415;
i=1=2*j+1, j=0, cos(1/power(10000, 0/4))=cos(1)=0.5403;
i=2=2*j, j=1, sin(1/power(10000, 2/4))=sin(1/100)=0.01;
i=3=2*j+1, j=1, cos(1/power(10000, 2/4))=cos(1/100)=1.0;
所以suis的位置编码为 (0.8415, 0.5403, 0.01, 1.0)。
pos=2:
i=0, sin(2/power(10000, 0/4)) = sin(2)=0.9093;
i=1, cos(2/power(10000, 0/4)) = cos(2) = -0.4161;
i=2, sin(2/power(10000, 2/4)) = sin(2/100) = 0.02;
i=3, cos(2/power(10000, 2/4)) = cos(2/100) = 1.0;
从而etudiant的位置编码为(0.9093, -0.4161, 0.02, 1.0)。
注意的一点是，位置编码没有梯度，不参与训练。（事先按照公式，定死的）
这种模式是什么样的？
在下图中，每行对应一个向量的位置编码。因此，第一行将是我们要添加到输入序列中第一个单词的嵌入的向量。每行包含512个值-每个值都在1到-1之间。我们已经对它们进行了颜色编码，因此图案可见。
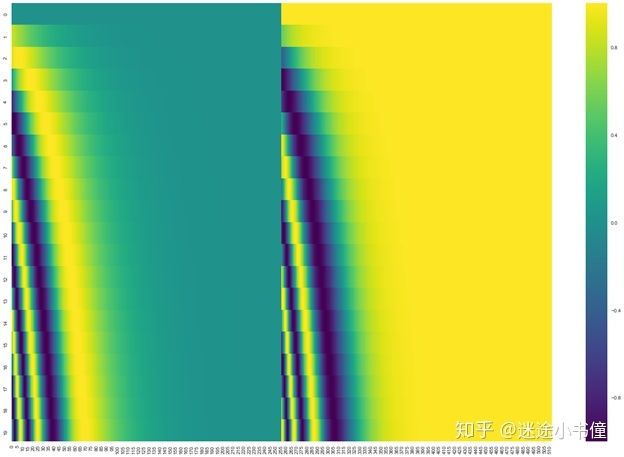
图25，（没有经过我自己检验的）嵌入大小为512（列）的20个单词（行）的位置编码的真实示例。您会看到它看起来像是在中心处分成两半。这是因为左半部分的值是由一个函数（使用正弦）生成的，而右半部分的值是由另一个函数（使用余弦）生成的。然后将它们串联起来以形成每个位置编码向量。
论文（第3.5节）中介绍了位置编码的公式。您可以在中看到用于生成位置编码的代码get_timing_signal_1d(https://github.com/tensorflow/tensor2tensor/blob/23bd23b9830059fbc349381b70d9429b5c40a139/tensor2tensor/layers/common_attention.py )。这不是唯一的位置编码方法。但是，它具有能够缩放到（训练阶段）看不见的序列长度的优点（例如，如果我们训练好的模型要求翻译的句子比训练集中的任何句子更长的长度）。
关于论文中的“位置编码”的补充检验（New）
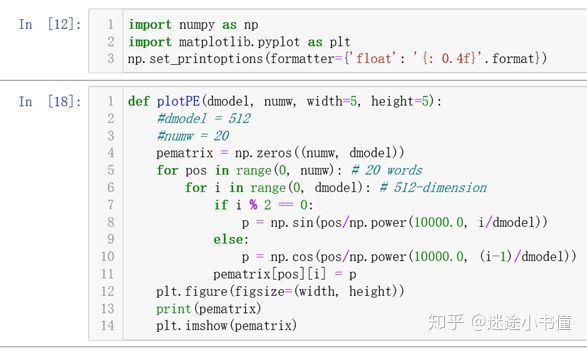
验证的代码如下：
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(formatter={'float': '{: 0.4f}'.format})
def plotPE(dmodel, numw, width=5, height=5):
#dmodel = 512
#numw = 20
pematrix = np.zeros((numw, dmodel))
for pos in range(0, numw): # 20 words
for i in range(0, dmodel): # 512-dimension
if i % 2 == 0:
p = np.sin(pos/np.power(10000.0, i/dmodel))
else:
p = np.cos(pos/np.power(10000.0, (i-1)/dmodel))
pematrix[pos][i] = p
plt.figure(figsize=(width, height))
print(pematrix)
plt.imshow(pematrix)
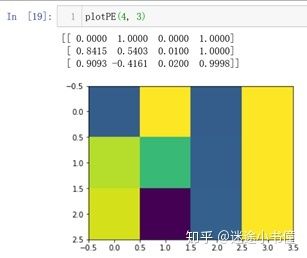
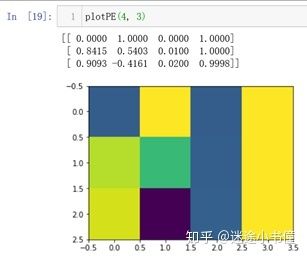
三个词，d_model=4的时候的表示，如上图所示。
plotPE(4, 3)
plotPE(512, 20, width=30, height=50) # almost no change after 200-dimension
plotPE(512, 200, width=30, height=30) # 200 words
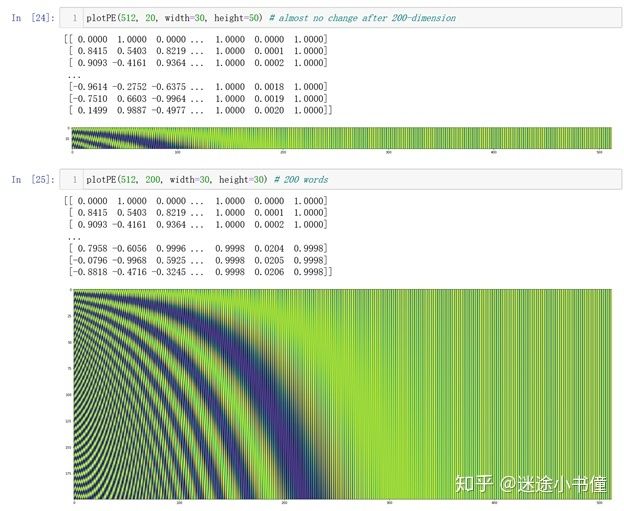
上面展示了20个词，以及200个词的时候的position encoding矩阵的示例。可以看到20个词的时候，基本上200维以后各个词的位置编码保持一致了。200个词的时候，350维之后的各个词的编码也基本保持一致了。关键的区分，在前半段。
残差
在继续进行示例之前，我们需要提到的编码器架构中的一个细节是，每个/层编码器中的每个子层（self-attention sublayer，feed forward neural network sublayer）在其周围都有残差连接，然后进行层归一化(layer normalization, https://arxiv.org/abs/1607.06450 )步骤。
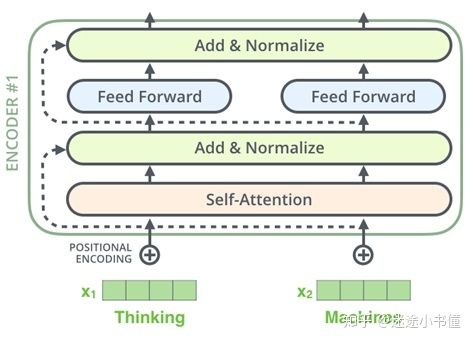
图26，残差计算的引入。
如果我们要可视化向量和与自注意力相关的layer-norm操作，它将看起来像这样：
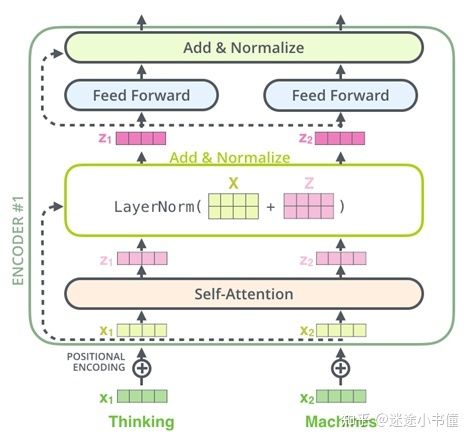
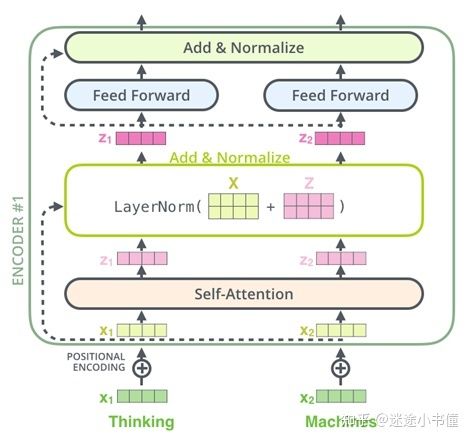图27，残差的具体计算时机的示例。
残差计算具体体现在上图的，LayerNorm(X+Z)的X+Z的部分，其中X代表的是叠加了位置编码的浅绿色矩阵，Z来自自注意力子层的输出，X和Z都是2行4列，所以可以进行element-wise相加，得到一个新的2行4列的矩阵，然后再进行LayerNorm操作。
执行完Add&Normalize操作后，得到深红色的矩阵Z，其两个行向量z1和z2会分别发送给feed forward层，执行进一步的操作计算。
假设，我们以位置编码向量为例，解释一下LayerNorm具体的操作(New)：
如前所述，Je的位置编码向量为（0, 1, 0, 1），suis的位置编码为 (0.8415, 0.5403, 0.01, 1.0)，etudiant的位置编码为(0.9093, -0.4161, 0.02, 1.0)。
那么，首先计算每个向量的mean和standard derivation，即均值和标准方差：
x=(0, 1, 0, 1) ->
numpy.mean(x)=0.5=(0+1+0+1)/4,
numpy.std=0.5=sqrt( (0-0.5)(0-0.5) + (1-0.5)(1-0.5) + (0-0.5)(0-0.5) + (1-0.5)(1-0.5)) / 4)=sqrt(0.25);
所以(x-mean)/std = (-0.5, 0.5, -0.5, 0.5)/0.5 = (-1, 1, -1, 1)。
同理，suis的位置编码为 (0.8415, 0.5403, 0.01, 1.0)对应的是[ 0.64519696 -0.15272266 -1.55755923 1.06508494]，etudiant的位置编码为(0.9093, -0.4161, 0.02, 1.0)对应的是[ 0.88873494 -1.32958763 -0.59968687 1.04053957]
这（位置编码）也适用于解码器的子层。如果我们想到一个由2个堆叠式编码器和解码器组成的Transformer，它看起来像这样：
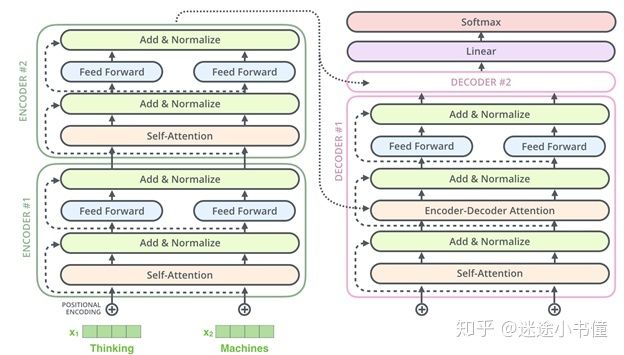
图28，开始引入decoder解码器部分。该图绘制出来了decoder #1的细节，decoder #2则高度抽象为一个box了。注意，编号应该从#0开始。
该图的细节，encoder的部分，已经比较清晰了。剩下的是decoder的部分，以及右上角的Linear和Softmax的部分。
解码器端
现在我们已经涵盖了编码器方面的大多数概念，我们基本上也知道了解码器的组件如何工作。但是，让我们看一下它们如何协同工作。
编码器首先处理输入序列。然后，顶部/顶层编码器的输出转换为注意力向量K和V的集合。每个解码器decoder将在其“编码器-解码器注意力层”（Encoder-Decoder Attention layer）中使用它们，这有助于解码器将注意力集中在输入序列中的适当位置：
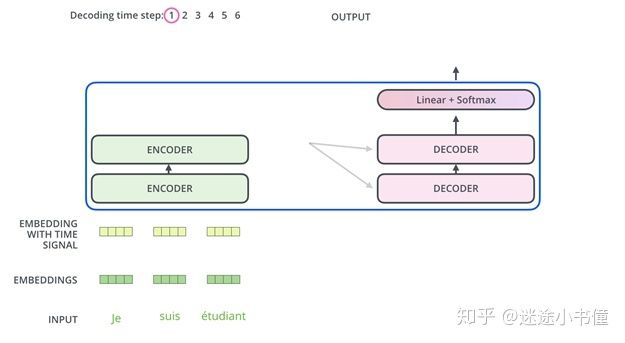
图29.1 开始综合考虑encoder和decoder。这里的图中，假设ENCODER一共两层，DECODER也是一共两层。注意，target序列需要一个起始符号，例如，来表示一个序列的开始！参考图30.1 ~ 30.5.
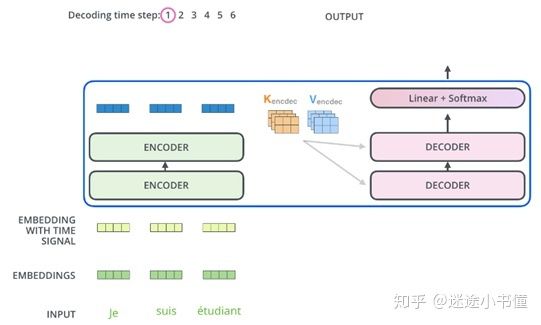
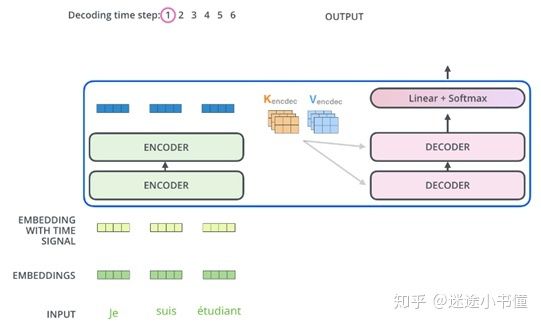
图29.2 准备好encoder的K和V矩阵，扔给decoder。这里的图中，假设ENCODER一共两层，DECODER也是一共两层。
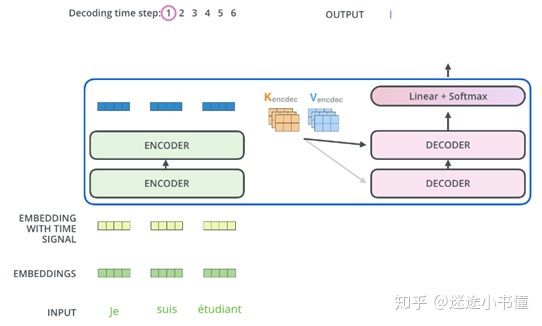
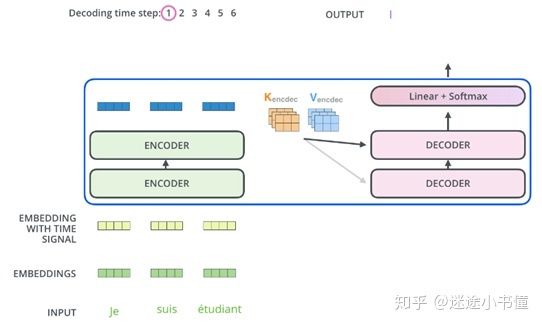
图29.3，接受来自encoder的K和V之后，decoder翻译产出了第一个词，I。完成编码阶段后，我们开始解码阶段。解码阶段的每个步骤都从输出序列中输出一个单词（此例子中，为被翻译出来的英语语句）。
以下步骤重复此过程，直到到达出现特殊符号
细化的训练数据的组织形式(new)：
（本示例参考：The Annotated Transformer: https://nlp.seas.harvard.edu/2018/04/03/attention.html ）
假设我们要训练一个copy transformer，其功能就是把输入原封不动地输出，例如假设输入是一个序列”1 2 3 4”，则我们期望输出也是”1 2 3 4”。
现在进入训练过程，假设我们有个batch（每个序列的第一个词”1”可以看成即start-of-sentence填充符号），为：
Src Trg
1,4,2,1 1,4,2
1,4,4,4 1,4,4
这里需要注意一下我们的输入training batch的样子，src部分是2行4列的一个矩阵，而trg部分是2行3列的一个矩阵！
我们的整体目标是根据：src和trg[:, :-1]
Src Trg[:, :-1]
1,4,2,1 1,4,2
1,4,4,4 1,4,4
来预测 trg[:, 1:]
Src Trg[:, 1:]
1,4,2,1 4,2,1
1,4,4,4 4,4,4
实际的，我们的训练过程其实是类似于：
第一步：给定src = [[1,4,2,1], [1,4,4,4]] 和 trg = [[1], [1]] 通过神经网络transformer得到：
trg=[[1, 4?], [1, 4?]]，这里给4打问号，是因为实际预测到的不一定是4，如果不是4，产生loss，计算loss，并反向传播。
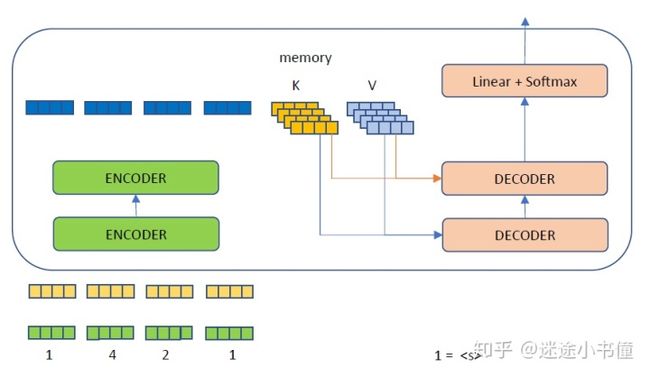
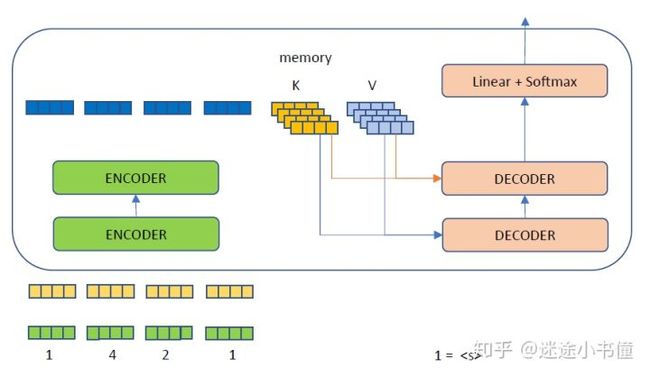
图30.1 开始解码的开始状态（假设现在是基于训练好的模型的“测试阶段”），编码器ENCODER端已经运行完毕，得到了source memory。Target序列的第一个单词，是事先给定的。
解码器这边，最初只有一个，作为句子的开始，对该词进行encode，然后参考来自ENCODER部分的memory, K, V来分别计算multi-head attention + feed forward，最后得到一个向量，对该向量进行linear + softmax,就是下一个词，例如4?。这里对4?打个问号是因为模型当前不一定能成功预测出来4.
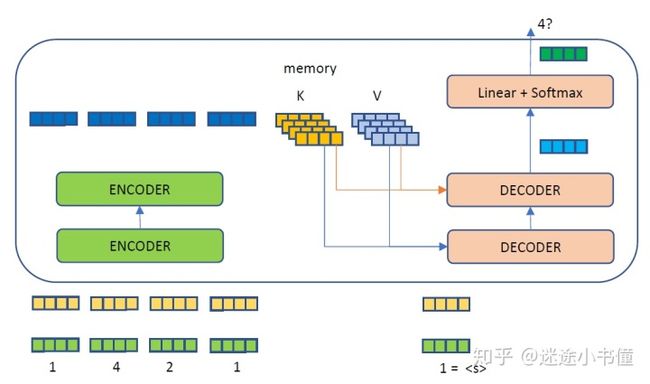
图30.2 解码器工作第一步，走一遍DECODERs和Linear+softmax生成器，然后得到一个预测出来的词4?。
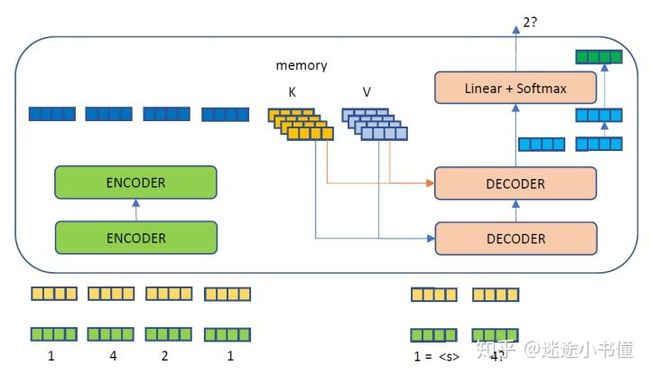
图30.3 解码器工作的第二步，根据已有的计算好的source memory和当前可用的target sequence来继续对下一个词预测。第二步，我们把得到的1，4?作为target sequence，扔给DECODER，其内部也同样参考已有的ENCODER的memory, K and K，来得到一个新的矩阵，我们取该矩阵的最后一行，扔给linear+softmax就得到下一个词，假设为2?。
图30.4. 第三步，我们把得到的”1，4?, 2?”作为target sequence，扔给DECODER，其内部也同样参考已有的ENCODER的memory, K and K，来得到一个新的矩阵，我们取该矩阵的最后一行，扔给linear+softmax就得到下一个词，假设为1?。这样的话，我们其实完成了“训练阶段”。
当然，训练阶段，不是分成三步，而是基于mask，一步搞定的，示例为：
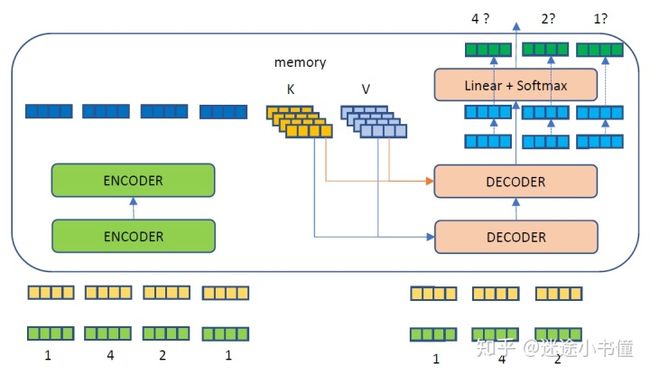
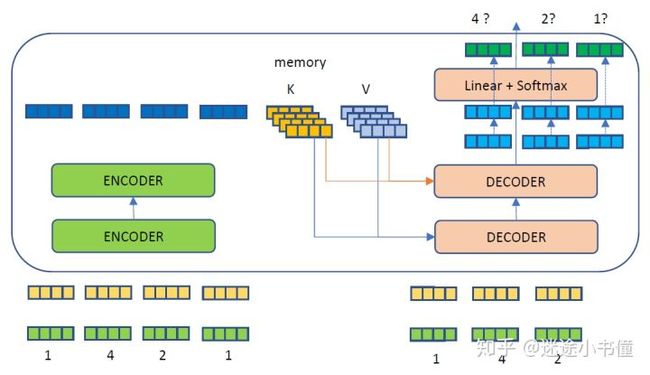
图30.5 训练阶段的“一步到位”（因为有target mask控制）。
训练阶段的一步到位，source序列为1,4,2,1，target序列为1,4,2带mask。目标是根据transformer，得到4?,2?,1?这个target序列。简化期间，类似于：
Input = source端的”s1, s4, s2, s1”和target端的”t1”从而有Output = t4?.
Input = source端的”s1, s4, s2, s1”和target端的”t1, t4”从而有Output = t4?, t2?.
Input = source端的”s1, s4, s2, s1”和target端的”t1, t4, t1”从而有 Output = t4?, t2?, t1?.
Mask相当于一个矩阵：
[[1, 0, 0], [1, 1, 0], [1, 1, 1]]。也就是说：
当预测t4（target序列的第二个词，第一个词是）的时候，只有t1可见；
当预测t2(target序列的第三个词)的时候，只有t1和t4可见（这里的t4，在模型训练阶段是batch给好的，知道是4；在实际模型测试阶段，是上一步预测出来的t4?（实际可能是4或者其他词））；
当预测t1（target序列的第四个词）的时候，只有t1, t4, 和t2可见。
这样的话，预测出来的序列，t4?, t2?, t1?就会进一步和事先知道的target序列的reference, t4, t2, t1进行对比，计算loss，并使用SGD/Adam等方法进行反向传播来更新transformer中的参数。
如下是原文中的示例，这里简单copy过来，不再详细说。细化的解码器和解码算法方面的示例：
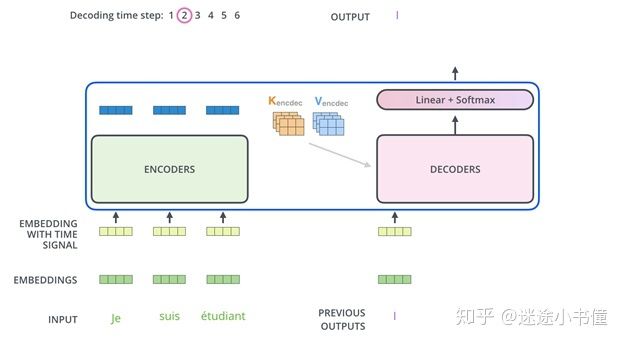
图31. 解码的例子。
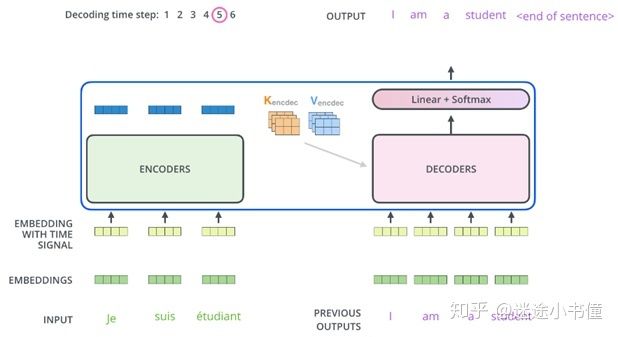
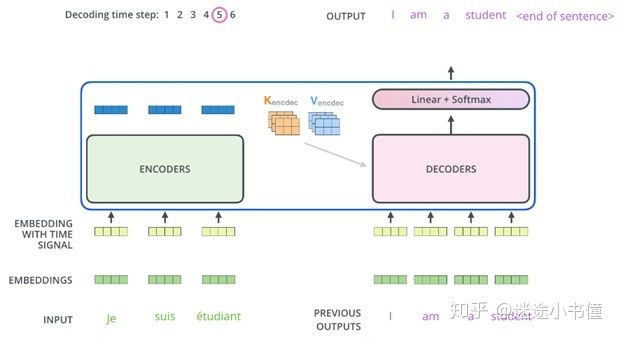
图32. 解码的例子。这里的，否则target sequence为空的前提下，无法触发DECODER工作。”I”显然不能作为default输入。
解码器中的自注意力层与编码器中的自注意力层略有不同：
在解码器中，仅允许自注意力层参与输出序列中的当前位置和其前面（左边）的位置。这是通过自注意力计算的时候，在softmax计算之前，根据mask 矩阵，把未来的（当前词右边的）向量设置为-inf来完成的。
“ Encoder-Decoder Attention”层的工作方式与多头自注意力类似，不同之处在于它从其decoder下一层创建其Queries矩阵，并从编码器encoder堆栈的输出中获取Keys和Values矩阵。
最终的线性层和Softmax层（生成器）
解码器堆栈（即，包括6层decoder layers的一个module）输出浮点数向量。我们如何把它变成一个词？这就是最后的线性层和其后的Softmax层的工作。
线性层是一个简单的全连接的神经网络，它将解码器堆栈产生的向量投影到一个更大的向量中，称为logits向量。（类似于one-hot-alike表示，只不过one-hot的是一个位置为1，其他位置都为0；而logits是一个位置的概率得分最大，其他的位置的值可以非0）
假设我们的模型从其学习的训练数据集中知道有10,000个去冗余后的英语单词（我们模型的“目标语言的词汇表”）。这将使logits向量的宽度变为10,000个单元-每个单元对应一个单词的分数。这就是我们对线性层模型输出的解释。
然后，softmax层将这些分数转换为概率（全部为正，全部相加为1.0）。选择具有最高概率的单元，并且与此单元对应的单词将作为该时间步的输出。
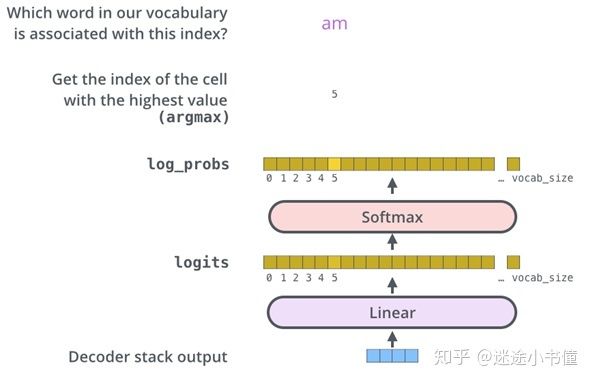
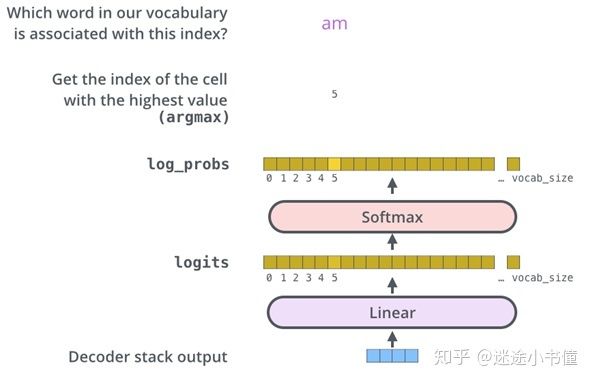图33. 生成器，一个线性层加一个softmax层。
该图从底部开始，将产生的向量作为解码器堆栈的输出。然后将其转换为输出单词。 因为下标从0开始，所以logits和log_probs的最右边一个词的下标应该是vocab_size-1 (error-fix)。特别的，当目标语言的词表过大的时候，例如100K，可以考虑sampled softmax算法来加速最后一步从logits到log_probs的计算，细节可以参考论文：http://www.iro.umontreal.ca/~lisa/pointeurs/importance_samplingIEEEtnn.pdf 和https://arxiv.org/pdf/1602.02410v1.pdf 。大部分深度学习平台上都有提供函数来直接计算sampled softmax，例如CNTK的https://www.cntk.ai/pythondocs/CNTK_207_Training_with_Sampled_Softmax.html；tensorflow的https://www.tensorflow.org/api_docs/python/tf/nn/sampled_softmax_loss , pytorch的一个实现https://github.com/leimao/Sampled_Softmax_PyTorch
训练回顾
既然我们已经通过训练过的Transformer涵盖了整个前向过程(forward pass process)，那么乍一看训练模型的直觉将非常有用。
在训练过程中，未经训练的模型将经过完全相同的前向过程。但是，由于我们在标记好的（也就是给定的双语句子对集合）训练数据集上对其进行训练，因此我们可以将其当前参数值下的模型输出与实际正确的输出进行比较。从而计算损失函数，并对每个参数的梯度使用随机梯度下降或者类似的扩展方法进行进一步的更新。
为了直观地说明这一点，我们假设输出词汇表仅包含六个词（“ a”，“ am”，“ i”，“ thanks”，“ student”和“
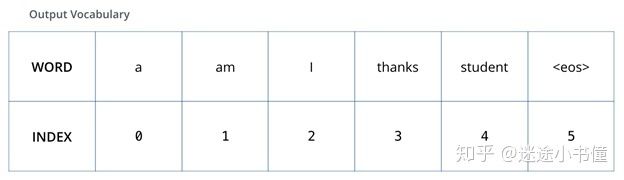
表1，我们的模型的输出词汇表是在我们开始训练之前的预处理阶段创建的。注意：这个表格不太好，最好有和(=
定义输出词汇表后，我们可以使用宽度相同的只包括0和1的向量来指示词汇表中的每个单词。这也称为one-hot编码。因此，例如，我们可以使用以下向量表示单词“ am”：
图34，示例：输出词汇表的单词”am”的one-hot编码 。
回顾之后，让我们讨论模型的损失函数-我们在训练阶段进行优化的度量标准，经过训练，我们希望可以得到惊喜的准确模型。
损失函数
假设我们正在训练我们的模型。假设这是我们训练阶段的第一步，我们正在以一个简单的示例对其进行训练-将“ merci”转换（翻译）为“ thank”。
这意味着我们希望，merci是输入的时候，输出的是一个表示单词“thank”的概率分布。但是，由于尚未对该模型进行训练，这不太可能发生。
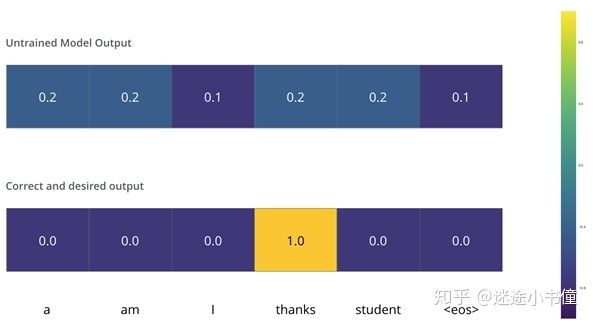
图35，由于模型的参数（权重）都是随机初始化的，因此（未经训练的）模型会针对每个单元格/单词生成具有任意值的概率分布。我们可以将其与实际输出进行比较，然后使用反向传播算法来调整所有模型的权重，以使模型输出(model’s output)更接近所需的参考输出(reference golden output)。
您如何比较两个概率分布？我们简单地从另一个中减去一个。有关更多详细信息，请参见 交叉熵(https://colah.github.io/posts/2015-09-Visual-Information/) 和Kullback-Leibler散度(https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained )。
但是请注意，这是一个过于简化的示例。实际上，我们将使用一个单词多于一个单词的句子作为一个输入。例如，输入：“ je suis étudiant”，预期输出：“I am a student”。这实际上意味着我们希望我们的模型连续输出概率分布，其中：
每个概率分布都由一个宽度为vocab_size的向量表示（在我们的玩具示例中为6，但更实际地为3,000或10,000或者更大）
第一概率分布向量中，与单词“ i”相关联的单元格具有最高概率
第二概率分布向量中，与单词“ am”相关联的单元格处具有最高概率
依此类推，直到第五个输出分布表示’
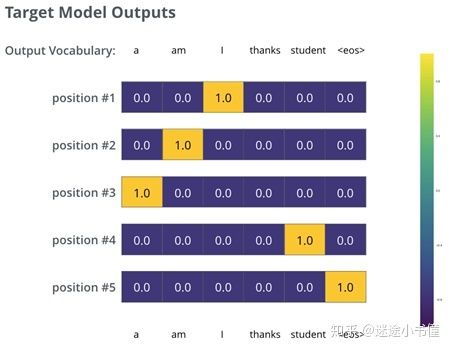
图36，目标概率分布示例：我们在模型训练中，使用一个个样本句子对(bilingual sentence pairs)对该概率分布进行训练。
在足够大的数据集上训练模型足够长的时间后，我们希望产生的概率分布如下所示：
图37，希望经过训练，该模型将输出我们期望的正确翻译。当然，这并不是该短语是否属于训练数据集的真正迹象（请参阅：交叉验证 https://www.youtube.com/watch?v=TIgfjmp-4BA ）。请注意，即使不太可能是该时间步长的输出，每个位置也会获得一定的概率值–这是softmax的一个非常有用的属性，可以帮助训练过程。
现在，由于该模型一次生成一个输出，因此我们可以假设该模型正在从该概率分布中选择具有最高概率的单词，然后丢弃其余单词。为做到这一点，有一种方法（称为贪婪解码）。做到这一点的另一种方法是，保留前两个单词（例如，“ I”和“ a”），然后在下一步中运行模型两次：一次假设第一个输出位置为单词“ I”，另一个假设第一个输出位置是单词“ a”，并且考虑到位置＃1和＃2都保留了较低的版本。我们在＃2和＃3等位置重复此操作。这种方法称为“beam search”，在我们的示例中，beam_size为2（因为我们在计算位置＃1和＃2的beam之后比较了结果），和top_beams也是两个（因为我们保留了两个词）。这两个都是您可以尝试调试的超参数(hyper parameter tuning)。
基于KL distance的损失函数计算的简要介绍(new)：
首先看一个batch里面只有一个句子的例子：
假设 目标P=[0.3, 0.6, 0.1]，而模型输出的是 Q=[0.4, 0.5, 0.05, 0.05]
这里P是3维的，Q是4维的，无法直接计算KLDivLoss。一种方法是pad P，例如
P=[0.3, 0.6, 0.1, 1e-9], 这样的话，就可以计算KLDivLoss了：
(P * (P/Q).log()).sum() -> 结果为0.0924
也可以直接调用KLDivLoss方法：
torch.nn.KLDivLoss(reduction=‘sum’)(Q.log(), P)
这里需要注意的是，KLDivLoss的第一个参数是log(model.output)，第二个参数是target reference tensor。
完整的代码如下：
python
>>> import torch
>>> from torch.autograd import Variable
>>> P = Variable(torch.FloatTensor([0.3, 0.6, 0.1, 1e-9]))
>>> Q = Variable(torch.FloatTensor([0.4, 0.5, 0.05, 0.05]))
>>> P = P.unsqueeze(0)
>>> Q = Q.unsqueeze(0)
>>> print (P, P.shape, Q, Q.shape)
tensor([[3.0000e-01, 6.0000e-01, 1.0000e-01, 1.0000e-09]]) torch.Size([1, 4]) tensor([[0.4000, 0.5000, 0.0500, 0.0500]]) torch.Size([1, 4])
>>> (P * (P/Q).log()).sum()
tensor(0.0924)
>>> torch.nn.KLDivLoss(reduction=‘sum’)(Q.log(), P)
tensor(0.0924)
有个潜在有意思的问题，就是在机器翻译中，基于当前训练中的模型，得到的model output的序列的长度（单词的个数）不一定和reference sequence的长度一致，这样的话，也是无法直接计算KL loss的。一个补足方法，就是把两者的长度拉到同一个数值上，例如：
1. 以reference sequence的长度为准，如果model output过长，则截取右边多出来的部分；如果过短，则补0。
2. 或者以model output的长度为准，对reference sequence进行长度的变更。
一般认为在KL loss下，第一种方案更好，因为有基于reference sequence的长度的制约。
Transformer进阶
我希望您已经发现这是一个有用的地方，可以开始用Transformer的主要概念打破僵局。如果您想更深入一点，建议采取以下步骤：
阅读“ 注意力就是您所需要的一切 Attention is All You Need https://arxiv.org/abs/1706.03762 ”论文，Transformer博客文章（《Transformer：一种用于语言理解的新型神经网络体系结构https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html 》）和Tensor2Tensor公告https://ai.googleblog.com/2017/06/accelerating-deep-learning-research.html 。
观看ŁukaszKaiser的演讲https://www.youtube.com/watch?v=rBCqOTEfxvg ，探讨模型及其细节
使用Tensor2Tensor存储库中提供的Jupyter Notebook探秘https://colab.research.google.com/github/tensorflow/tensor2tensor/blob/master/tensor2tensor/notebooks/hello_t2t.ipynb
探索Tensor2Tensor repo https://github.com/tensorflow/tensor2tensor
· 后续工作：
· Depthwise Separable Convolutions for Neural Machine Translation
· One Model To Learn Them All
· Discrete Autoencoders for Sequence Models
· Generating Wikipedia by Summarizing Long Sequences
· Image Transformer
· Training Tips for the Transformer Model
· Self-Attention with Relative Position Representations
· Fast Decoding in Sequence Models using Discrete Latent Variables
· Adafactor: Adaptive Learning Rates with Sublinear Memory Cost
英文原版来自：Alammar，Jay（2018）。示例化Transformer[博客文章]。取自https://jalammar.github.io/illustrated-transformer/。
快速导航：