GraphSage -《Inductive Representation Learning on Large Graphs》论文详解
目录
- 前言
- GraphSAGE算法
-
- Embedding生成算法
- 聚合函数
- 固定大小邻居采样
- GraphSAGE参数学习
-
- 无监督学习
- 理论分析(案例研究)
- 附录(作者简介)
前言
之前在推荐排序上开发的一个算法,取得了不错的效果。其中就用到了图神经网络模块,该模块的一部分思想源于GraphSage和GATs,因此对GraphSage的算法及代码理解还是比较深的,本文对GraphSage算法部分进行剖析。
先说GraphSage的几个特点:
- GraphSage是Induction框架。(这一点区别于基于Transduction的kipf-GCN,关于Induction和Transduction请参考博文《Transductive Learning 和 Inductive Learning》);
- GraphSage不为图中每一个节点学习单独的embedding,而是学习一个聚合函数,该函数通过从节点的本地邻域中抽样和聚合特征来生成节点embedding。(这一点和kipf-GCN不同,kipf-GCN是直接为节点学习embedding)
- GraphSage利用节点特征信息(例如,文本属性、节点配置文件信息、节点度)来学习泛化到不可见节点的嵌入函数。
- GraphSage可以利用所有图中存在的结构特征(如节点度),所以也可以应用于没有节点特征的图。
- GraphSage设计了一个无监督损失函数,允许在没有特定任务监督的情况下进行训练。
GraphSAGE算法
Embedding生成算法
本节假设模型已经训练好,且参数已经固定。此时GraphSage模型学到了:
- K K K 个聚合函数(aggregator functions) A G G R E G A T E k AGGREGATE_k AGGREGATEk, ∀ k ∈ { 1 , … , K } \forall k\in\{1,\ldots,K\} ∀k∈{1,…,K},它从邻居节点聚合信息。
- 权重矩阵 W k W^k Wk, ∀ k ∈ { 1 , … , K } \forall k\in\{1,\ldots,K\} ∀k∈{1,…,K},用于在模型的不同层之间传播信息,或称为“search depth”。
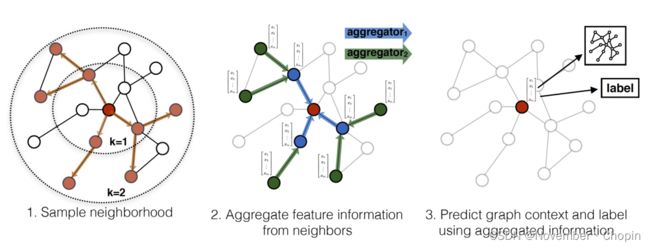
算法1的直觉是:在每次迭代或搜索深度时,节点从它们的局部邻居那里聚合信息,随着这个过程的迭代,节点从图中以自身为中心的更远处逐渐获得越来越多的信息。
算法1描述了在整个图 G = ( V , E ) \mathcal{G=(V,E)} G=(V,E) 和所有节点的特征 x v , ∀ v ∈ V \bold{x}_v,\,\forall v\in \mathcal{V} xv,∀v∈V 作为输入的情况下,embedding生成过程。下面将描述如何将其推广到mini-batch的情况。
- 输入:
- k k k 表示当前外循环的step(步数,也表示搜索深度,即搜索了 k k k 阶邻居);
- h k \bold{h}^k hk 表示在 k k k step 上的节点表示,其中 h v 0 = x v \bold{h}_v^0=\bold{x}_v hv0=xv 。
- 第1步: (第4行) 每个节点 v ∈ V v\in\mathcal{V} v∈V 将它的直接邻居节点的表示 { h u k − 1 , ∀ u ∈ N ( v ) } \{\bold{h}_u^{k-1},\,\forall u\in\mathcal{N}(v)\} {huk−1,∀u∈N(v)} 聚合为一个向量 h N ( v ) k − 1 \bold{h}_{\mathcal{N(v)}}^{k-1} hN(v)k−1。这个聚合步骤依赖于在外循环的先前迭代中生成的表示(即 k − 1 k−1 k−1),并且 k = 0 k=0 k=0 表示被定义为输入节点特征。
- 第2步: (第5行) 将聚合的邻居表示 h N ( v ) k − 1 \bold{h}_{\mathcal{N(v)}}^{k-1} hN(v)k−1 与当前节点的表示 h v k − 1 \bold{h}_v^{k-1} hvk−1 进行concat并送入全连接层中(权重为 W k \bold{W}^k Wk ),生成下一次循环需要的节点表示 h v k \bold{h}_v^{k} hvk。
- 第3步: 如果内循环未结束,则进入第1步,直接使用 h v k \bold{h}_v^{k} hvk 作为节点 v v v 的特征用于生成其他节点表示(如作为其他节点的邻域节点);如果是内循环结束,(第7行) 则将 h v k \bold{h}_v^{k} hvk 进行原地标准化 h v k / ∥ h v k ∥ 2 \bold{h}_v^{k}/\lVert \bold{h}_v^{k} \rVert_2 hvk/∥hvk∥2,进入第4步。
- 第4步: 如果外循环未结束,将第3步生成的 h v k \bold{h}_v^{k} hvk 用于 k + 1 k+1 k+1 阶节点表示的生成,进入第1步。如果外循环结束,(第9行) 则将第3步生成的节点表示作为节点的最终输出。
第3步聚合邻居节点所用到的聚合函数 A G G R E G A T E k AGGREGATE_k AGGREGATEk 有很多形式,参见聚合函数一节。
扩展到mini-batch:给定一组输入节点,首先采样 K K K 阶邻居集合,然后执行内循环,与第3行不同的是,不是遍历所有节点,而是只计算满足每个深度递归所需的节点表示。(mini-batch的详细过程及伪码在作者给的Appendix中!)
聚合函数
由于图中节点的邻居节点不像图像、句子那样有顺序,因此算法1中的聚合函数必须能在是无序的向量集中运行。理想情况下,聚合器函数不受输入序列的改变而改变并且具有较高的泛化性能。作者在实验了三个聚合函数:
- 均值聚合器(Mean aggregator)。即取直接邻居节点的表示 { h u k − 1 , ∀ u ∈ N ( v ) } \{\bold{h}_u^{k-1},\,\forall u\in\mathcal{N}(v)\} {huk−1,∀u∈N(v)} 的均值。均值聚合器几乎等同于kipf-GCN框架中使用的卷积传播规则。 算法1中的第4行和第5行替换为以下内容来导出GCN方法的Inductive变体:
h v k ← σ ( W ⋅ M E A N ( { h v k − 1 } ∪ { h u k − 1 , ∀ u ∈ N ( v ) } ) ) \begin{align} \bold{h}_v^k\,\leftarrow\,\sigma\Bigg(\bold{W}\cdot MEAN\Big( \{\bold{h}_v^{k-1}\} \cup \{\bold{h}_u^{k-1},\,\forall u\in\mathcal{N}(v)\} \Big) \Bigg) \end{align} hvk←σ(W⋅MEAN({hvk−1}∪{huk−1,∀u∈N(v)})) 作者称这种对均值聚合器的改进为卷积,因为它是局部谱卷积的粗略、线性的近似(这一点须要理解!!!)。这个卷积聚合器和论文提出的其他聚合器之间的一个重要区别是它不执行算法1第5行中的 c o n c a t concat concat 操作。这种 c o n c a t concat concat 可以被视为不同搜索深度或者层之间的类似于resnet中的“跳跃连接(skip connection)”,它带来了显著的提升。 - LSTM聚合器(LSTM aggregator)。与平均聚合器相比,LSTM具有更大的表达能力的优势。但LSTM是非对称的,因为不同输入顺序会带来不同输出。作者通过简单地将LSTM应用于节点邻居的随机排列来调整LSTM以在无序集上的操作。
- 池化聚合器(Pooling aggregator)。池化聚合器既是对称的又是可训练的,其中节点的每个邻居的向量先通过全连接层然后再进行元素级的 max-pooling :
A G G R E G A T E k p o o l = m a x ( { σ ( W p o o l h u i k + b ) , ∀ u i ∈ N ( v ) } ) \begin{align} AGGREGATE_k^{pool}=max\Big( \{ \sigma(W_{pool}\bold{h}_{u_i}^{k}+b), \forall u_i\in\mathcal{N}(v) \} \Big) \end{align} AGGREGATEkpool=max({σ(Wpoolhuik+b),∀ui∈N(v)}) 其中, m a x max max 表示element-wise max操作符; σ \sigma σ 表示激活函数。
最大池化前可以有任意个全连接层。MLP可以被认为是一组函数,为邻居节点集合中的每个节点表示计算特征。 通过将max-pooling 用于每个计算特征,模型有效地捕获了邻居节点集合的不同方面。此外,作者在实验中发现max-pooling和mean-pooling之间没有显著差异。
补充:Graph采用 均值聚合器 可以处理可变大小的输入,而由于池化聚合器中使用了全连接层,所以只能使用固定数量的采样邻居!!!(2022.10.13)
固定大小邻居采样
GraphSage 均匀采样一组固定大小的邻居,而不是在算法1中使用完整的邻居集。即:
v v v 的邻域 N ( v ) \mathcal{N}(\mathcal{v}) N(v) 是从 v v v 的直接邻居 { u ∈ V : ( u , v ) ∈ E } \{u\in\mathcal{V}:(u,v)\in\mathcal{E}\} {u∈V:(u,v)∈E} 中固定大小的均匀采样(这个固定大小有一定的讲究,在平时的实践中,根据节点平均度的大小选取合适的采样大小,我平时一般取平均度的2~4倍)。
这是为了保持每个batch有固定的计算量。算法1的邻域在每个batch及层次 k k k 都会进行不同的均匀采样,如果没有这个采样,单个批处理的内存和预期运行时是不可预测的,并且在最坏情况下达到 O ( ∣ V ∣ ) \mathcal{O}(|\mathcal{V}|) O(∣V∣)。 相比之下,GraphSAGE的每批空间和时间复杂度固定为 O ( ∏ i = 1 K S i ) \mathcal{O}(\prod_{i=1}^{K}S_i) O(∏i=1KSi), S i S_i Si 和 K K K 是超参数。实践中,作者发现GraphSage在 K = 2 K=2 K=2 且 S 1 ⋅ S 2 ≤ 500 S_1\cdot S_2\le500 S1⋅S2≤500 达到高性能。作者在文中实验的参数大致为 K = 2 K=2 K=2, S 1 = 25 S_1=25 S1=25, S 2 = 10 S_2=10 S2=10,设置 S 1 < S 2 S_1
GraphSAGE参数学习
无监督学习
基于图的损失函数鼓励邻近的节点具有相似的表示,同时强制不同的节点的表示有很高的区分:
J G ( z u ) = − l o g ( σ ( z u T z v ) ) − Q ⋅ E v n ∼ P n l o g ( σ ( − z u T z v n ) ) \begin{align} J_{\mathcal{G}}(\mathbf{z}_u)=-log\bigg(\sigma\Big({\mathbf{z}_u}^T{\mathbf{z}_v}\Big)\bigg) -Q\cdot\mathbb{E}_{v_n\sim P_n}log\bigg(\sigma\Big(-{\mathbf{z}_u}^T{\mathbf{z}_{v_n}}\Big)\bigg) \end{align} JG(zu)=−log(σ(zuTzv))−Q⋅Evn∼Pnlog(σ(−zuTzvn)) 其中,其中 v v v 是在定长随机游走中共同出现在 u u u 附近的节点; σ \sigma σ 是sigmoid函数; P n P_n Pn 是负样本的抽样分布; Q Q Q 定义了负样本的个数。
传入到损失函数中的 z u \bold{z}_u zu 的表示是从邻居节点的特征中生成的,而不是为每一个节点训练一个embedding。
通过梯度下降法优化上式的损失函数,就可以获得调优的层间权重 W k W^k Wk 及聚合器中的权重。
理论分析(案例研究)
这一节,探讨GraphSage的表达能力,以便深度了解GraphSage如何学习图结构,尽管GraphSage本质上是基于特征的。
本节考虑GraphSage是否可以学习并预测节点的聚类系数(Wiki百科-clustering coefficient),可以参考博文《图论中的聚类系数(Clustering coefficient)简单介绍》来理解。作者证明,算法1能够将聚类系数逼近到任意精度:
定理 1:设 x v ∈ U , ∀ v ∈ V \bold{x}_v\in U, \forall v\in\mathcal{V} xv∈U,∀v∈V 表示算法1在图 G \mathcal{G} G 上的输入特征, U U U 表示 R d \mathbb{R}^d Rd 上的任意紧致子集。假设存在一个正的定(fixed)常数 C ∈ R + C\in\mathbb{R}^+ C∈R+ 使得 ∥ x v − x v ′ ∥ > C \lVert \bold{x}_v-\bold{x}_{v'} \rVert>C ∥xv−xv′∥>C 适用于所有节点对(pairs of nodes)。则对于 ∀ ϵ > 0 \forall \epsilon>0 ∀ϵ>0 存在参数设置 Θ ∗ \mathbf{\Theta}^* Θ∗ 对于算法1中 K = 4 K=4 K=4 迭代次数之后,有:
∣ z v − c v ∣ < ϵ , ∀ v ∈ V , |z_v-c_v|<\epsilon, \forall v\in\mathcal{V}\,, ∣zv−cv∣<ϵ,∀v∈V, 其中, z v ∈ R z_v\in\mathbb{R} zv∈R 是算法1 生成的最终输出值, c v c_v cv 是节点聚合系数。
定理 1 指出,对于任何图,算法 1 都存在一个参数设置,如果每个节点的特征都是不同的(并且如果模型足够高维),它可以将该图中的聚类系数逼近到任意精度。
本定理证明待续…
附录(作者简介)
William L. Hamilton:麦吉尔大学计算机科学兼职教授,也是Citadel LLC的高级定量研究员。
Rex Ying(应智韬):耶鲁大学计算机科学系的助理教授,斯坦福大学获得了计算机科学博士学位。
Jure Leskovec:斯坦福大学计算机科学副教授,也是Chan Zuckerberg Biohub(陈·扎克伯格生物中心)的研究员。