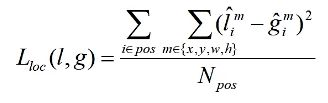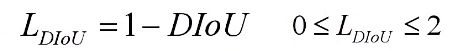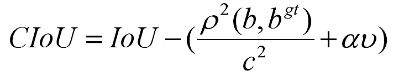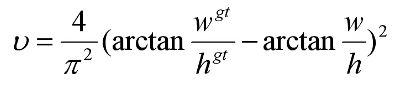目标检测:YOLO中的Moxaic-SPP-CIoU
一、Mosaic图像增强:实际就是多张图片拼接,送入网络训练的过程
1)增加了数据多样性
2)增加了目标个数
3)BN能一次性统计多张图片的参数。(Batch size本应设大一点,统计的均值方差参数才更接近总体的,但由于显存大小等因素,Batch size通常比较小)
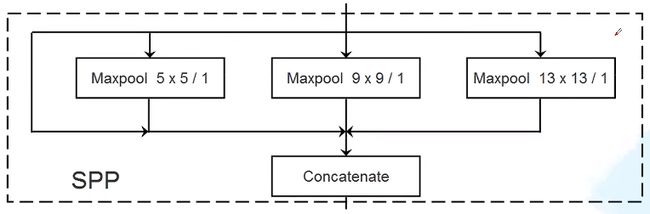
二、SPP(spatial pyramid pooling)模块:实现了不同尺度的特征融合
网络结构上YOLO-V3-SPP和YOLO-V3的差别就在于下图中加入了SPP模块。
SPP结构如下
SPP结构实际上就是不同尺度特征图的融合。4个分支的通道数相同,所有concat之后,通道数变为之前的4倍。
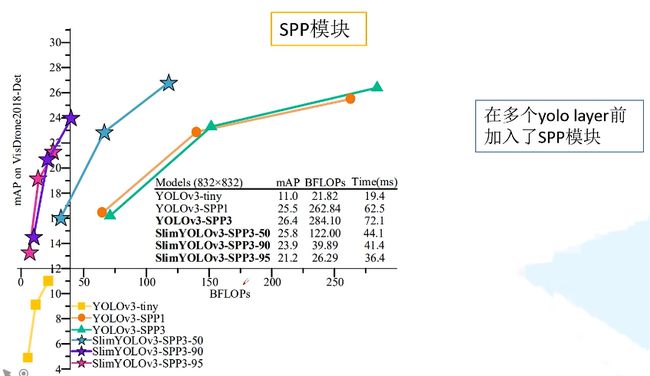
SPP结构为什么只在最小特征图的预测之前那一层加,另两个大的特征图预测之前为何不加。也可以,对比如下图YOLOv3-SPP1和YOLOv3-SPP3的对比。
三、定位损失:
之前的定位损失都是误差平方的计算,即L2损失。
新的损失都是基于IoU的损失。
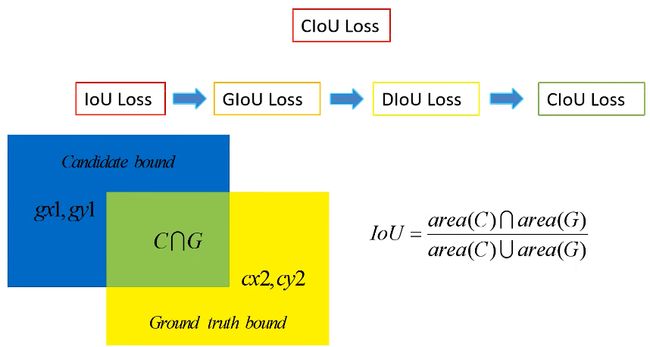
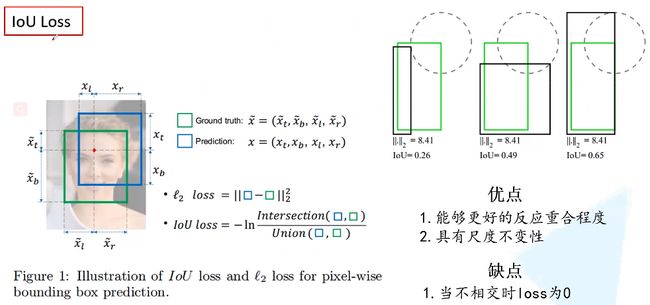
1、IoU损失
IoU就是我们所说的交并比,是目标检测中最常用的指标,在anchor-based的方法中,他的作用不仅用来确定正样本和负样本,还可以用来评价输出框(predict box)和ground-truth的距离。
1)优点
a)可以说它可以反映预测检测框与真实检测框的重合程度。
b)还有一个很好的特性就是尺度不变性,也就是对尺度不敏感(scale invariant), 在regression任务中,判断predict box和gt的距离最直接的指标就是IoU。(满足非负性;同一性;对称性;三角不等性)
2)缺点
a)如果两个框没有相交,根据定义,IoU=0,不能反映两者的距离大小(重合度)。同时因为loss=0,没有梯度回传,无法进行学习训练。
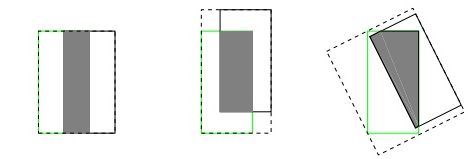
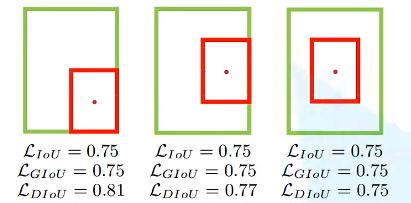
b)IoU无法精确的反映两者的重合度大小。如下图所示,三种情况IoU都相等,但看得出来他们的重合度是不一样的,左边的图回归的效果最好,右边的最差。
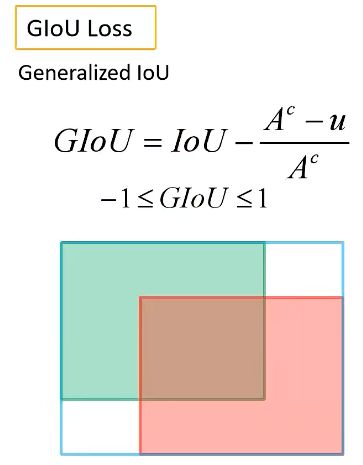
2、GIoU
计算公式中Ac为两个框外接矩形的面积,u是两个框并集的面积。
当两个框完全重合时,GIoU为1。当两个框相距无穷远时,GIoU为-1。
GIoU Loss的定义如下:
1)优点:
a)与IoU相似,GIoU也是一种距离度量,作为损失函数的话,GIoU Loss满足损失函数的基本要求;
b)GIoU对scale不敏感;
c)GIoU是IoU的下界,在两个框无限重合的情况下,IoU=GIoU=1;
d)IoU取值[0,1],但GIoU有对称区间,取值范围[-1,1]。在两者重合的时候取最大值1,在两者无交集且无限远的时候取最小值-1,因此GIoU是一个非常好的距离度量指标;
e)与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。
2)缺点:
当两个框如图同高水平重合,或同宽竖直重合时,GIoU退化成了IoU。
3、DIoU损失
作者认为IoU损失和GIoU损失有两个问题:
1)收敛的很慢;
2)回归的不够准确。
基于IoU和GIoU存在的问题,作者提出了两个问题:
1)直接最小化anchor框与目标框之间的归一化距离是否可行,以达到更快的收敛速度?
2)如何使回归在与目标框有重叠甚至包含时更准确、更快?
下图中分别显示了GIoU Loss和DIoU Loss在目标边界框迭代回归时,迭代次数和位置的关系。由图可见:DIoU Loss迭代收敛速度明显快于GIoU。
下图中三种情况下,IoU和GIoU都相同,但是三种情况下重合的效果明显不同,而DIoU却能有效的反映这个效果。
DIoU定义:
DIoU Loss定义:
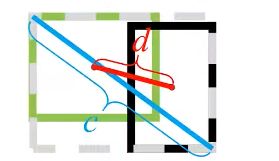
其中,b,bgt分别代表了预测框和真实框的中心点,且ρ代表的是计算两个中心点间的欧式距离。c代表的是能够同时包含预测框和真实框的外接矩形的对角线距离。
当两个框重合时,DIoU=IoU=1
当两个框距离无穷远时,DIoU=-1
DIoU损失能够直接最小化两个框之间的距离,所以收敛的速度更快。
DIoU还可以替换普通的IoU评价策略,应用于NMS中,使得NMS得到的结果更加合理和有效。
4、CIoU损失
作者认为一个好的回归定位损失应该考虑到3中几何参数:重叠面积,中心点距离,长宽比。考虑到长宽比还没被考虑到计算中,因此,进一步在DIoU的基础上提出了CIoU。其惩罚项如下面公式:
其中v用来度量长宽比的相似性,其定义如下:
CIoU Loss定义:
四、Focal Loss
One-stage目标检测模型样本不均衡:一张图像中能够匹配到目标的候选框(正样本)个数一般只有十几个或几十个,而没匹配到的候选框(负样本)大概有10k-100k个。在着10k-100k个未匹配到目标的候选框中大部分都是简单易分的负样本(对训练网络起不到什么作用,但由于数量太多会淹没掉少数但有助于训练的样本)。
不用所有负样本来训练,只用难度比较大的负样本???