pytorch深度学习实战lesson20
第二十课 卷积层的多输入和多输出通道
目录
理论部分
多输入通道
多输出通道
实践部分
理论部分
多输入通道
假设图片大小是200*200的话,那么用张量表示这个图片的话就是200*200*3,因为彩色图片是由红、绿、蓝三个通道构成的,因此表示一个彩色图片的时候要将这三原色的信息也给表示出来。
那么舒润有多个通道的话要怎么计算呢?
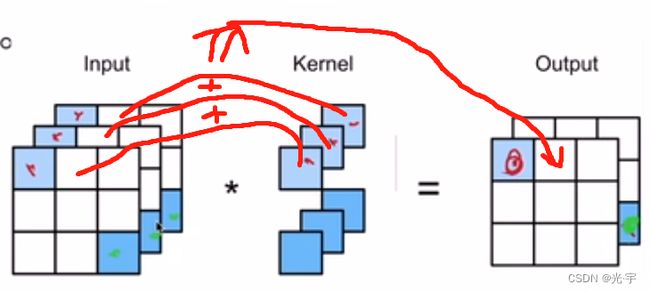
多通道的话就是每个通道都做次卷积,卷积核的维度是一样的,但是数值不一定是一样的。每个通道算完卷积后,如上图所示,再把卷积的计算结果加在一起。符号语言如下图所示:
多输出通道
多输出通道的话,对于下图来说也就是红框的部分多了一维。
为什么要设置多输入通道和多输出通道?
因为每个输出通道都可以识别特定的模式;而每个输入通道可以识别并组合输入中的模式,输入通道把输入输入进去后网络会为输入数据匹配相应的权重,来判断哪些重要哪些不重要。
对于多输入输出通道的底层神经网络,越底层它输出的东西越抽象,可能是一幅图片的纹理,但上层的网络在将底层网络加权求和后,它会把重要的纹理或信息拼接到一起,最终形成猫脚,最最终形成一只猫。
这个1*1的卷积核不会去看通道里面的空间模式,因为1*1的卷积核只是看输入数据的单独一个像素,它不会看像素周围的一圈其他像素。
如下我画的图所示,一个1*1的卷积层其实可以等价成一个全连接层。
实践部分
代码:
#多输入多输出通道
#实现一下多输入通道互相关运算
import torch
from d2l import torch as d2l
#多通道输入
def corr2d_multi_in(X, K):#二维互相关运算处理多通道输入函数
#对输入通道进行遍历拿出各个输入通道的每个小矩阵再做互相关运算,再按元素求和得到最终的结果(单通道输出)
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
#验证互相关运算的输出
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
print(corr2d_multi_in(X, K))#多通道输入,单通道输出
#多通道输出
#计算多个通道的输出的互相关函数
def corr2d_multi_in_out(X, K):
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)#多通道输出,把上面的输出堆叠起来,形成多通道输出
K = torch.stack((K, K + 1, K + 2), 0)
print(K.shape)
print(corr2d_multi_in_out(X, K))
print('#######################################################################')
#1*1卷积在全连接层(矩阵乘法)的实现以及直接实现
#1x1卷积
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
print(X.shape)
c_o = K.shape[0]
X = X.reshape((c_i, h * w))
K = K.reshape((c_o, c_i))
Y = torch.matmul(K, X)
return Y.reshape((c_o, h, w))
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))#输出通道为2,输入通道为3
Y1 = corr2d_multi_in_out_1x1(X, K)#全连接的实现(矩阵乘法)
Y2 = corr2d_multi_in_out(X, K)
print(X,'\n',K,'\n',Y1,'\n',Y2)
print(float(torch.abs(Y1 - Y2).sum()) < 1e-6)#说明他近似于0.也就是Y1Y2差不多。tensor([[ 56., 72.],
[104., 120.]])
torch.Size([3, 2, 2, 2])
tensor([[[ 56., 72.],
[104., 120.]],[[ 76., 100.],
[148., 172.]],[[ 96., 128.],
[192., 224.]]])
#######################################################################
torch.Size([3, 3, 3])
tensor([[[-1.6313, 0.0887, 0.6206],
[-1.4196, -1.1524, -0.8890],
[ 1.5420, -0.4402, 3.1655]],[[ 0.4326, -0.7483, -0.4302],
[-1.0683, -0.5747, -0.5555],
[ 0.7052, -0.6912, 0.7018]],[[ 0.2094, 0.3906, -1.5985],
[ 0.8189, -1.6181, -2.3361],
[ 0.3077, -0.8393, -0.3554]]])
tensor([[[[-0.4711]],[[ 0.4921]],
[[ 1.3620]]],
[[[ 1.2301]],[[ 1.3347]],
[[ 0.6919]]]])
tensor([[[ 1.2667, 0.1219, -2.6813],
[ 1.2585, -1.9437, -3.0362],
[ 0.0395, -1.2759, -1.6301]],[[-1.2844, -0.6194, -0.9168],
[-2.6055, -3.3042, -3.4514],
[ 3.0509, -2.0447, 4.5847]]])
tensor([[[ 1.2667, 0.1219, -2.6813],
[ 1.2585, -1.9437, -3.0362],
[ 0.0395, -1.2759, -1.6301]],[[-1.2844, -0.6194, -0.9168],
[-2.6055, -3.3042, -3.4514],
[ 3.0509, -2.0447, 4.5847]]])
True