统计学习方法笔记（一）：感知机

统计学习方法笔记（一）：感知机

前言：本文是基于李航老师《统计学习方法》的笔记 ~

感知机学习的目的：求出将训练数据进行线性划分的分离超平面。

1. 感知机模型：

1.1 数学形式：

$$f(x)=sign(w\cdot x+b)$$

其中输入空间为$XϵR^n$，输出空间为$Y=\left\{\begin{array}{c}+1,-1\end{array}\right\}$。w和b为感知机模型参数，$wϵR^n$叫做权值或权值向量，$bϵR$叫做偏置，$w\cdot x$表示w和x的内积。sign是符号函数，即
$$sign(x)=\left\{\begin{array}{cc}& +1,x>=0\\ & -1,x<0\end{array}\right\}$$

1.2 几何解释：

分离超平面：线性方程
$$w\cdot x+b=0$$
对应于特征空间$R^n$中的一个超平面S（分离超平面），其中w是超平面的法向量，b是超平面的截距。这个超平面将特征空间划分为两部分，且这两部分的点分别被分为正、负两类。如下图所示：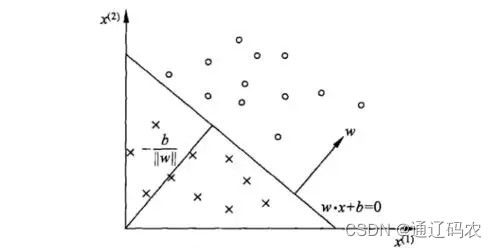

2. 学习策略

2.1 数据集——线性可分性

数据集是否线性可分，即为是否存在某个超平面S可以将该数据集中所有的实例点完全正确地划分到超平面两侧。可以完全正确的划分，则该数据集为线性可分数据集；否则，则为线性不可分。

即给定数据集$T=\left\{\begin{array}{c}(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\end{array}\right\}$，其中$x_iϵX=R^n$，$y_iϵY=\left\{\begin{array}{c}+1,-1\end{array}\right\}$，$i=1,2,...,N$。若为线性可分数据集，则对于所有$y_i=+1$的实例$i$，有$w\cdot x_i+b>0$；对所有$y_i=-1$的实例$i$，有$w\cdot x_i+b<0$。

2.2 学习策略

• 学习策略：这里为定义（经验）损失函数并将损失函数极小化。

• 损失函数：$L(w,b)=-{\sum }_{x_iϵM}^{}{y}_i(w\cdot x_i+b)$

  其中，$M$为误分类点的集合。

  损失函数推导过程：

  • 首先，写出输入空间$R^n$中任意一点$x_0$到超平面$S$的距离：
    $$\frac{1}{\Vert w\Vert }|w\cdot x_0+b|$$
    这里$\Vert w\Vert$是$w$的$L_2$范数。

  • 对于误分类的数据$(x_i,y_i)$来说，
    $$-y_i(w\cdot x_i+b)>0$$
    成立。因为当$(w\cdot x+b)>0$时，$y_i=-1$；而当$(w\cdot x+b)<0$时，$y_i=+1$。因此，误分类点$x_i$到超平面$S$的距离是：
    $$-\frac{1}{\Vert w\Vert }{y}_i(w\cdot x_i+b)$$
    （因为$|y_i|=+1$，所以$-y_i(w\cdot x_i+b)=|w\cdot x_i+b|$）

  • 那么假设超平面$S$的误分类点集合为$M$，那么所有误分类点到超平面$S$的总距离为：
    $$-\frac{1}{\Vert w\Vert }\sum _{x_iϵM}{y}_i(w\cdot x_i+b)$$
    不考虑$\frac{1}{\Vert w\Vert }$，就得到感知机学习的损失函数。

3. 感知机学习算法：

3.1 原始形式

• 基本想法：求感知机模型的参数$w,b$，使其为如下损失函数极小化问题的解
  $$mi{n}_{w,b}^{}L(w,b)=-\sum _{x_iϵM}{y}_i(w\cdot x_i+b)$$

• 具体方法：随机梯度下降法。

  即用梯度下降法不断地极小化目标函数（损失函数$L(w,b)$），但这个极小化过程我们不是一次使$M$中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

  • 损失函数$L(w,b)$的梯度：由 ${▽}_{w}L(w,b)=-{\sum }_{x_iϵM}{y}_i{x}_i$ 和 ${▽}_{b}L(w,b)=-{\sum }_{x_iϵM}{y}_i$ 给出（分别对$L(w,b)$的$w$和$b$参数求偏导获得）。

  • 极小化过程具体为：每次随机选取一个误分类点$(x_i,y_i)$，对$w,b$进行更新：
    $$\begin{gathered} w\leftarrow w+\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$
    上式中$\eta (0<\eta \le 0)$是步长，又称为学习率。

    这样，通过迭代可以使得损失函数$L(w,b)$不断减小，直到为0。此时，我们就获得了感知机的分离超平面，此时的参数$w,b$也即感知机模型的参数。

• 输入：训练数据集$T=\left\{\begin{array}{c}(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\end{array}\right\}$，其中$x_iϵX=R^n$，$y_iϵY=\left\{\begin{array}{c}-1,+1\end{array}\right\}$，$i=1,2,...,N$；学习率$\eta (0<\eta ⩽1)$。

• 输出：$w,b$，感知机模型$f(x)=sign(w\cdot x+b)$

• 算法流程：

  • 选取初值$w_0,b_0$（即任意选取一个超平面$w_0,b_0$）

  • 在训练集中随意选取一个误分类点$(x_i,y_i)$；

  • 如果$y_i(w\cdot x_i+b)⩽0$，对$w$和$b$进行更新：
    $$\begin{gathered} w\leftarrow w+\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$

  • 重复第二、三步算法，直至训练集中没有误分类点（即对于所有的点$(x_i,y_i)$，都有$y_i(w\cdot x_i+b)>0$）

• 代码实现（基于typeScript）

  // 导入所需常用函数
  import {
      Get_Matrix_shape,
      Get_Zero_Matrix,
      Matrix_Item_Sum,
      Matrix_Dot_Multiplication,
      Matrix_Add_Each,
      Matrix_Multiplication_Number
  } from "./universal-func"
  
  // 代码正文
  let x = [[3, 3], [4, 3], [1, 1]]
  let y = [1, 1, -1]
  let x_shape = Get_Matrix_shape(x)
  let y_shape = Get_Matrix_shape(y)
  // 初始化 w, b (初始化为0)，学习率n初始化为 1
  let w = Get_Zero_Matrix(x_shape.slice(1))
  let b = 0
  let n = 1
  // 其它数据
  let index = 0 // 当前的x的子矩阵序号
  let sum = 0 // 当前符合 y(w·x + b) > 0 的x子矩阵的个数
  while(sum < x_shape[0]){
      // 求解 y(w·x + b)
      if(y[index] * (Matrix_Item_Sum(Matrix_Dot_Multiplication(w, x[index])) + b) <= 0){
          w = Matrix_Add_Each(w, Matrix_Multiplication_Number(n * y[index], x[index]))
          b += n * y[index]
          sum = -1
      }
  
      index = ((index + 1) % x_shape[0])
      sum += 1
  }
  console.log("w: ", w)
  console.log("b: ", b)
  

  其中引用的相关函数：

  /**
   * @Get_Matrix_shape 获取矩阵的行列数，也即矩阵的 shape（形状）
   * @matrix 矩阵
   */
  export function Get_Matrix_shape(matrix: any){
      let shape_list = [matrix.length]
      if(matrix[0] && Array.isArray(matrix[0])){
          shape_list.push(...Get_Matrix_shape(matrix[0]))
      }
      return shape_list
  }
  
  /**
   * @Get_Zero_Matrix 按指定形状创建一个 零矩阵
   * @shape 矩阵shape形状数组
   */
  export function Get_Zero_Matrix(shape: number[]){
      let matrix: any = []
      if(shape.length === 1){
          for(let i = 0; i < shape[0]; i++){
              matrix.push(0)
          }
      } else {
          for(let i = 0; i < shape[0]; i++){
              matrix.push(Get_Zero_Matrix(shape.slice(1)))
          }
      }
      return matrix
  }
  
  /**
   * @Matrix_Dot_Multiplication 求两矩阵点乘 (二阶矩阵点乘)
   * @param x1、x2: 要点乘的两个矩阵
   */
  export function Matrix_Dot_Multiplication(x1: any, x2: any){
      let x1_shape = Get_Matrix_shape(x1)
      let x2_shape = Get_Matrix_shape(x2)
      let matrix: any = []
      // 一维矩阵
      if(x1_shape.length === 1){
          if(x1_shape[0] === x2_shape[0]){
              for(let i = 0; i < x1_shape[0]; i++){
                  matrix.push(x1[i] * x2[i])
              }
          }
          return matrix
      }
  
      // 二维矩阵
      // 相关变量
      let similar_num = 0 // 行列相同的总数
      let index = -1 // 相似的行列的序号
      for(let i = 0; i < 2; i++){
          if(x1_shape[i] === x2_shape[i]){
              similar_num += 1
              index = i
          }
      }
      let x_l = [], x_r = []
      if(similar_num === 1){
          if(x1_shape[1 - index] === 1){
              x_l = [...x1]
              x_r = [...x2]
          } else if(x2_shape[1 - index] === 1){
              x_l = [...x2]
              x_r = [...x1]
          } else {
              return matrix
          }
          if(index === 0){
              for(let i = 0; i < x_r.length; i++){
                  let mid_matrix = []
                  for(let j = 0; j < x_r[0].length; j++){
                      mid_matrix.push(x_l[i][0] * x_r[i][j])
                  }
                  matrix.push(mid_matrix)
              }
          }else{
              for(let i = 0; i < x_r.length; i++){
                  let mid_matrix = []
                  for(let j = 0; j < x_r[0].length; j++){
                      mid_matrix.push(x_l[0][j] * x_r[i][j])
                  }
                  matrix.push(mid_matrix)
              }
          }
      } else if(similar_num === 2){
          for(let i = 0; i < x1_shape[0]; i++){
              let mid_matrix = []
              for(let j = 0; j < x1_shape[1]; j++){
                  mid_matrix.push(x1[i][j] * x2[i][j])
              }
              matrix.push(mid_matrix)
          }
      }
      return matrix
  }
  
  /**
   * @Matrix_Item_Sum 求矩阵各元素之和
   * @param matrix 要被求和的矩阵
   */
  export function Matrix_Item_Sum(matrix: any){
      let shape = Get_Matrix_shape(matrix)
      let sum = 0
      if(shape.length === 1){
          for(let i = 0; i < shape[0]; i++){
              sum += matrix[i]
          }
      } else {
          for(let i = 0; i < shape[0]; i++){
              sum += Matrix_Item_Sum(matrix[i])
          }
      }
      return sum
  }
  
  /**
   * @Matrix_Multiplication_Number 常数点乘矩阵
   * @param number_ 常数
   * @param matrix 矩阵
   */
  export function Matrix_Multiplication_Number(number_: number, matrix: any){
      let shape = Get_Matrix_shape(matrix)
      let m: any = []
      if(shape.length === 1){
          for(let i = 0; i < shape[0]; i++){
              m.push(matrix[i] * number_)
          }
      } else {
          for(let i = 0; i < shape[0]; i++){
              m.push(Matrix_Multiplication_Number(number_, matrix[i]))
          }
      }
      return m
  }
  
  /**
   * @Matrix_Add_Each 两矩阵相加函数
   * @param x1 矩阵1
   * @param x2 矩阵2
   */
  export function Matrix_Add_Each(x1: any, x2: any){
      let x1_shape = Get_Matrix_shape(x1)
      let matrix: any = []
      if(x1_shape.length === 1){
          for(let i = 0; i < x1_shape[0]; i++){
              matrix.push(x1[i] + x2[i])
          }
      } else {
          for(let i = 0; i < x1_shape[0]; i++){
              matrix.push(Matrix_Add_Each(x1[i], x2[i]))
          }
      }
      return matrix
  }
  

3.2 对偶形式

• 基本想法：将$w$和$b$表示为实例$x_i$和标记$y_i$的线性组合的形式，通过求解其系数而求得$w$和$b$。

  • 为不失一般性，假设初始值$w_0$，$b_0$均为0。对误分类点通过
    $$\begin{gathered} w\leftarrow w+\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$
    逐步修改$w$，$b$。

  • 设修改$n$次，则$w$，$b$关于$(x_i,y_i)$的增量分别是$a_i{y}_i{x}_i$和$a_i{y}_i$，这里$a_i=n_i\eta$，$n_i$是点$(x_i,y_i)$被误分类的次数。这里最后学习到的$w$，$b$可以表示为
    $$\begin{gathered} w=\sum _{i=1}^N{a}_i{y}_i{x}_i \\ b=\sum _{i=1}^N{a}_i{y}_i \end{gathered}$$
    这里$a_i\ge 0$，$i=1,2,...,N$，当$\eta =1$时，表示第$i$个实例点由于误分而进行更新的次数。实例点更新次数越多，意味着它距离分离超平面越近，也就越难分类（也就是说，这样的实例对学习结果影响最大）

• 输入：线性可分的数据集$T=\left\{\begin{array}{c}(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\end{array}\right\}$，其中$x_i\in R^n$，$y_i\in \left\{\begin{array}{c}-1,+1\end{array}\right\}$，$i=1,2,...,N$；学习率$\eta (0<\eta \le 1)$。

• 输出：$a$，$b$；感知机模型$f(x)=sign({\sum }_{j=1}^N{a}_j{y}_j{x}_j\cdot x+b)$，其中$a=(a_1,a_2,...,a_N{)}^T$。

• 算法流程：

  • 初始化$a\leftarrow 0$，$b\leftarrow 0$。

  • 在训练集中选取数据$(x_i,y_i)$。

  • 如果$y_i({\sum }_{j=1}^N{a}_j{y}_j{x}_j\cdot x_i+b)\le 0$，
    $$\begin{gathered} a_i\leftarrow a_i+\eta \\ b\leftarrow b+\eta y_i \end{gathered}$$

  • 转至第二步，直到没有误分类数据。

由于对偶形式中训练实例仅以内积（$x_j\cdot x_i$）的形式出现。为便于求解，我们可以先将训练集实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵
$$G=[x_i\cdot x_j{]}_{N\times N}$$

• 代码实现：

  let x = [[3, 3], [4, 3], [1, 1]]
  let y = [1, 1, -1]
  let x_shape = Get_Matrix_shape(x)
  // 获取Gram矩阵
  let G = Get_Gram_Matrix(x)
  // 相关参数n
  let n = 1
  // 初始化a和b
  let a = Get_Zero_Matrix([x_shape[0]])
  let b = 0
  // 相关参数
  let index = 0
  let sum = 0
  while(sum < x_shape[0]){
      let mid_num = 0
      for(let i = 0; i < x_shape[0]; i++){
          mid_num += (a[i] * y[i] * G[i][index])
      }
      if(y[index] * (mid_num + b) <= 0){
          a[index] += n
          b += (n * y[index])
          sum = -1
      }
      index = (index + 1) % x_shape[0]
      sum += 1
  }
  
  // 求w
  let w = Get_Zero_Matrix([x_shape[1]])
  for(let i = 0; i < x_shape[0]; i++){
      w = Matrix_Add_Each(w, Matrix_Multiplication_Number(a[i] * y[i], x[i]))
  }
  
  console.log(w)
  console.log(b)
  

  其中的相关函数

  /**
   * @Get_Matrix_shape 获取矩阵的行列数，也即矩阵的 shape（形状）
   * @matrix 矩阵
   */
  export function Get_Matrix_shape(matrix: any){
      let shape_list = [matrix.length]
      if(matrix[0] && Array.isArray(matrix[0])){
          shape_list.push(...Get_Matrix_shape(matrix[0]))
      }
      return shape_list
  }
  
  /**
   * @Get_Gram_Matrix 获取矩阵的Gram矩阵
   * @param matrix 
   */
  export function Get_Gram_Matrix(matrix: any){
      let Gram_matrix: any = []
      let shape = Get_Matrix_shape(matrix)
      for(let i = 0; i < shape[0]; i++){
          Gram_matrix.push([])
          for(let j = 0; j < shape[0]; j++){
              Gram_matrix[i].push(Get_Matrix_Transvection(matrix[i], matrix[j]))
          }
      }
      return Gram_matrix
  }
  
  /**
   * @Get_Matrix_Transvection 求两矩阵的内积(x1与x2的内积)
   * @param x1 
   * @param x2 
   */
  export function Get_Matrix_Transvection(x1: any, x2: any){
      // 两number变量，直接返回其乘法值
      if(!Array.isArray(x1)){
          return x1 * x2
      }
  
      let x1_shape = Get_Matrix_shape(x1)
      let x2_shape = Get_Matrix_shape(x2)
      // 内积值
      let sum_num = 0
      let matrix: any = []
      // 一维矩阵
      if(x1_shape.length === 1){
          if(x1_shape[0] === x2_shape[0]){
              for(let i = 0; i < x1_shape[0]; i++){
                  sum_num += (x1[i] * x2[i])
              }
          }
          return sum_num
      }
  
      // 二维矩阵
      // 相关变量
      let similar_num = 0 // 行列相同的总数
      let index = -1 // 相似的行列的序号
      for(let i = 0; i < 2; i++){
          if(x1_shape[i] === x2_shape[i]){
              similar_num += 1
              index = i
          }
      }
      let x_l = [], x_r = []
      if(similar_num === 1){
          if(x1_shape[1 - index] === 1){
              x_l = [...x1]
              x_r = [...x2]
          } else if(x2_shape[1 - index] === 1){
              x_l = [...x2]
              x_r = [...x1]
          } else {
              return sum_num
          }
          if(index === 0){
              for(let i = 0; i < x_r.length; i++){
                  for(let j = 0; j < x_r[0].length; j++){
                      sum_num += (x_l[i][0] * x_r[i][j])
                  }
              }
          }else{
              for(let i = 0; i < x_r.length; i++){
                  for(let j = 0; j < x_r[0].length; j++){
                      sum_num += (x_l[0][j] * x_r[i][j])
                  }
              }
          }
      } else if(similar_num === 2){
          for(let i = 0; i < x1_shape[0]; i++){
              for(let j = 0; j < x1_shape[1]; j++){
                  sum_num += (x1[i][j] * x2[i][j])
              }
          }
      }
      return sum_num
  }
  
  /**
   * @Get_Zero_Matrix 按指定形状创建一个 零矩阵
   * @shape 矩阵shape形状数组
   */
  export function Get_Zero_Matrix(shape: number[]){
      let matrix: any = []
      if(shape.length === 1){
          for(let i = 0; i < shape[0]; i++){
              matrix.push(0)
          }
      } else {
          for(let i = 0; i < shape[0]; i++){
              matrix.push(Get_Zero_Matrix(shape.slice(1)))
          }
      }
      return matrix
  }
  
  /**
   * @Matrix_Add_Each 两矩阵相加函数
   * @param x1 矩阵1
   * @param x2 矩阵2
   */
  export function Matrix_Add_Each(x1: any, x2: any){
      let x1_shape = Get_Matrix_shape(x1)
      let matrix: any = []
      if(x1_shape.length === 1){
          for(let i = 0; i < x1_shape[0]; i++){
              matrix.push(x1[i] + x2[i])
          }
      } else {
          for(let i = 0; i < x1_shape[0]; i++){
              matrix.push(Matrix_Add_Each(x1[i], x2[i]))
          }
      }
      return matrix
  }
  
  /**
   * @Matrix_Multiplication_Number 常数点乘矩阵
   * @param number_ 常数
   * @param matrix 矩阵
   */
  export function Matrix_Multiplication_Number(number_: number, matrix: any){
      let shape = Get_Matrix_shape(matrix)
      let m: any = []
      if(shape.length === 1){
          for(let i = 0; i < shape[0]; i++){
              m.push(matrix[i] * number_)
          }
      } else {
          for(let i = 0; i < shape[0]; i++){
              m.push(Matrix_Multiplication_Number(number_, matrix[i]))
          }
      }
      return m
  }
  

4. 补充：

4.1 $L_2$范数

向量所有元素的平方和的开平方。

即对于$n$维特征$X=(x_1,x_2,...,x_n)$，其$L_2$范数为：
$${\Vert X\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$