反对称矩阵的特征值及性质
目录
- 写在前面
- 结论
- 反对称矩阵
- 反对称矩阵的特征值是0或纯虚数
-
- 由性质推导
- 实例推导
- 3x3的反对称矩阵秩为2
- 参考
- 完
写在前面
1、文中所有资源、参考已给出来源链接,如有侵权请联系删除
2、码字不易,转载本文请注明出处,本文链接:https://blog.csdn.net/qq_41102371/article/details/115734924
结论
1、反对称矩阵的特征值是0或纯虚数
2、3x3的反对称矩阵可作为一个向量的叉乘矩阵
3、3x3的反对称矩阵的秩为2
反对称矩阵
设 A = ( a i j ) n × n A=(a_{ij})_{n{\times}n} A=(aij)n×n,若其中元素满足 a i j = a j i , ∀ i , j ⇔ A T = A a_{ij}=a_{ji},\forall i,j{\Leftrightarrow}A^T=A aij=aji,∀i,j⇔AT=A,则称 A A A是对称矩阵;若其元素满足 a i j = − a j i , ∀ i , j ⇔ A T = − A a_{ij}=-a_{ji},\forall i,j{\Leftrightarrow}A^T=-A aij=−aji,∀i,j⇔AT=−A ,则称A为反对称矩阵[1]。
若A是反对称矩阵,则 a i j = − a j i a_{ij}=-a_{ji} aij=−aji,当 i = j i=j i=j时,便有 a i i = 0 a_{ii}=0 aii=0,即反对称矩阵主对角线上的元全为零,而位于主对角线两侧对称的元反号。
于是对于n阶方阵 A A A,当 A = − A T A=-A^T A=−AT时 A A A是反对称矩阵,例如
A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] A=\begin{bmatrix} 0 & -a_3& a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} A=⎣⎡0a3−a2−a30a1a2−a10⎦⎤
很明显A是一个反对称矩阵,反对称矩阵及其性质有什么用呢,一个很实际的例子就是《计算机视觉中的多视图几何》(三维重建相关)P406中的叉乘矩阵是一个n=3的反对称矩阵[2]:

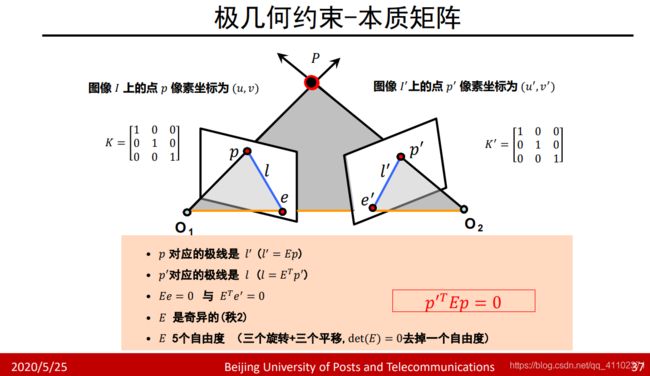
并且n=3的反对称矩阵的性质影响着structure from motion(sfm)中的本质矩阵E的性质[3],比如n=3的反对称矩阵秩为2,因此E矩阵秩也为2
反对称矩阵的特征值是0或纯虚数
由性质推导
[1]设实反对称矩阵A的特征值为 λ = a + b i ( i = − 1 ) \lambda=a+bi(i=\sqrt{-1}) λ=a+bi(i=−1)(为什么设置为虚数呢,因为当虚部为0时包含了实数)
,相应的特征值向量 x = u + v i ≠ 0 x=u+vi\neq0 x=u+vi=0 ,其中 u , v u,v u,v是非零实向量。那么由 A x = λ x Ax={\lambda}x Ax=λx得到
A ( u + v i ) = ( ) a + b i ( u + v i ) A(u+vi)=()a+bi(u+vi) A(u+vi)=()a+bi(u+vi)
即
A u + i A v = ( a u − b v ) + ( b u + a v ) i Au+iAv=(au-bv)+(bu+av)i Au+iAv=(au−bv)+(bu+av)i
令实部虚部分别相等,则有
A u = a u − b v , A v = b u + a v Au=au-bv,Av=bu+av Au=au−bv,Av=bu+av
于是
u T A u = a u T u − b u T v u^TAu=au^Tu-bu^Tv uTAu=auTu−buTv
v T A v = b v T u + a v T v v^TAv=bv^Tu+av^Tv vTAv=bvTu+avTv
因为 u T v = v T u = ( u , v ) u^Tv=v^Tu=(u,v) uTv=vTu=(u,v)(u,v的內积),则上述2个式子相加得到
u T A u + v T A v = a ( ∣ u ∣ 2 + ∣ v ∣ 2 ) u^TAu+v^TAv=a\left( {\left\vert u\right\vert}^2 + {\left\vert v \right\vert}^2\right) uTAu+vTAv=a(∣u∣2+∣v∣2)
又因为
u T A u ∈ C , A = − A T u^TAu\ {\in}\ C,\ A=-A^T uTAu ∈ C, A=−AT
u T A u u^TAu uTAu是一个数,把它看成一个1x1的矩阵,它的转置就是本身,所以
u T A u = ( u T A u ) T = u T A T u = − u T A u u^TAu=(u^TAu)^T=u^TA^Tu=-u^TAu uTAu=(uTAu)T=uTATu=−uTAu
⇒ u T A u = − u T A u \Rightarrow u^TAu=-u^TAu ⇒uTAu=−uTAu
只有0的相反数才是0,于是
u T A u = 0 u^TAu=0 uTAu=0
同理
v T A v = 0 v^TAv=0 vTAv=0
因此
u T A u + v T A v = a ( ∣ u ∣ 2 + ∣ v ∣ 2 ) = 0 u^TAu+v^TAv=a\left( {\left\vert u\right\vert}^2 + {\left\vert v \right\vert}^2\right)=0 uTAu+vTAv=a(∣u∣2+∣v∣2)=0
则
u + v i ≠ 0 ⇒ ∣ u ∣ 2 + ∣ v ∣ 2 ≠ 0 ⇒ a = 0 u+vi\neq0 \Rightarrow {\left\vert u\right\vert}^2 + {\left\vert v \right\vert}^2\neq0 \Rightarrow a=0 u+vi=0⇒∣u∣2+∣v∣2=0⇒a=0
从而 λ = a + b i = b i \lambda=a+bi=bi λ=a+bi=bi,b为任意实数,当 b = 0 b=0 b=0时,特征值 λ = b i = 0 \lambda=bi=0 λ=bi=0,当 b ≠ 0 b\neq0 b=0时, λ = b i \lambda=bi λ=bi为纯虚数
因此反对称矩阵的特征值是0或纯虚数
并且由上 b ≠ 0 b\neq0 b=0时, λ \lambda λ为纯虚数,有 A u = − b v , A v = b u Au=-bv,Av=bu Au=−bv,Av=bu即
u = b − 1 A v , v = − b − 1 A u u=b^{-1}Av,v=-b^{-1}Au u=b−1Av,v=−b−1Au
于是
∣ u ∣ 2 = u T u = u T b − 1 A v = b − 1 u T A v {\left\vert u \right\vert}^2=u^Tu=u^Tb^{-1}Av=b^{-1}u^TAv ∣u∣2=uTu=uTb−1Av=b−1uTAv
∣ v ∣ 2 = v T v = − v T b − 1 v T A u = b − 1 v T A u = b − 1 ( u T A v ) T {\left\vert v \right\vert}^2=v^Tv=-v^Tb^{-1}v^TAu=b^{-1}v^TAu=b^{-1}(u^TAv)^T ∣v∣2=vTv=−vTb−1vTAu=b−1vTAu=b−1(uTAv)T
因为 u T A v = ( u T A v ) T u^TAv=(u^TAv)^T uTAv=(uTAv)T,所以 ∣ u ∣ 2 = ∣ v ∣ 2 {\left\vert u \right\vert}^2={\left\vert v \right\vert}^2 ∣u∣2=∣v∣2
此外,由 u T A u = 0 u^TAu=0 uTAu=0以及 u T v = u T ( b − 1 A u ) = − b − 1 u T A u u^Tv=u^T(b^{-1}Au)=-b^{-1}u^TAu uTv=uT(b−1Au)=−b−1uTAu可知 u T v = 0 u^Tv=0 uTv=0,即 u , v u,v u,v正交
这证明了反对称矩阵对应于纯虚数的特征向量的实部和虚部形成的实向量等长且互相正交。
实例推导
令 A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] 令A=\begin{bmatrix} 0 & -a_3& a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} 令A=⎣⎡0a3−a2−a30a1a2−a10⎦⎤
用特征值的计算方法[4]来直接计算
∣ [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] − [ λ 0 0 0 λ 0 0 0 λ ] ∣ = ∣ − λ − a 3 a 2 a 3 − λ − a 1 − a 2 a 1 − λ ∣ \left\vert{ \begin{bmatrix} 0 & -a_3& a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix}- \\ \begin{bmatrix} \lambda &0& 0\\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix} }\right\vert = \begin{vmatrix} -\lambda & -a_3& a_2 \\ a_3 & -\lambda & -a_1 \\ -a_2 & a_1 & -\lambda \end{vmatrix} ∣∣∣∣∣∣⎣⎡0a3−a2−a30a1a2−a10⎦⎤−⎣⎡λ000λ000λ⎦⎤∣∣∣∣∣∣=∣∣∣∣∣∣−λa3−a2−a3−λa1a2−a1−λ∣∣∣∣∣∣
于是有
− λ ( λ 2 + a 1 2 ) + a 3 ( − λ a 3 − a 1 a 2 ) + a 2 ( a 1 a 3 − λ a 2 2 ) = 0 -\lambda({\lambda}^2+{a_1}^2)+{a_3}({-\lambda}a_3-a_1a_2)+a_2(a_1a_3-{\lambda}{a_2}^2)=0 −λ(λ2+a12)+a3(−λa3−a1a2)+a2(a1a3−λa22)=0
⇒ − λ 3 − λ a 1 2 − λ a 3 2 − a 1 a 2 a 3 + a 1 a 2 a 3 − λ a 2 2 = 0 {\Rightarrow} - {\lambda}^3 - {\lambda}{a_1}^2-{\lambda}{a_3}^2-{a_1a_2a_3}+{a_1a_2a_3}-{\lambda}{a_2}^2=0 ⇒−λ3−λa12−λa32−a1a2a3+a1a2a3−λa22=0
⇒ − λ ( λ 2 + a 1 2 + a 2 2 + a 3 2 ) = 0 {\Rightarrow}-{\lambda}({\lambda}^2+{a_1}^2+{a_2}^2+{a_3}^2)=0 ⇒−λ(λ2+a12+a22+a32)=0
⇒ λ = 0 , 或 λ 2 + a 1 2 + a 2 2 + a 3 2 = 0 {\Rightarrow} {\lambda}=0, 或{\lambda}^2+{a_1}^2+{a_2}^2+{a_3}^2=0 ⇒λ=0,或λ2+a12+a22+a32=0
λ 2 = − ( a 1 2 + a 2 2 + a 3 2 ) = − m {\lambda}^2=-({a_1}^2+{a_2}^2+{a_3}^2)=-m λ2=−(a12+a22+a32)=−m
因为 m = a 1 2 + a 2 2 + a 3 2 > 0 m={a_1}^2+{a_2}^2+{a_3}^2>0 m=a12+a22+a32>0
所以 λ = m ∗ − 1 {\lambda}=\sqrt{m} * \sqrt{-1} λ=m∗−1,此时为纯虚数
3x3的反对称矩阵秩为2
同样, 令 A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] 令A=\begin{bmatrix} 0 & -a_3& a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} 令A=⎣⎡0a3−a2−a30a1a2−a10⎦⎤
对矩阵 A A A做初等行变换,矩阵的秩不变
交换行顺序
[ a 3 0 − a 1 − a 2 a 1 0 0 − a 3 a 2 ] \begin{bmatrix} a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0\\ 0 & -a_3 & a_2 \\ \end{bmatrix} ⎣⎡a3−a200a1−a3−a10a2⎦⎤
第一行乘以 a 2 a_2 a2,第二行乘以 a 3 a_3 a3再加上第一行
[ a 2 a 3 0 − a 1 a 2 − a 2 a 3 a 1 a 3 0 0 − a 3 a 2 ] ⇒ [ a 2 a 3 0 − a 1 a 2 0 a 1 a 3 − a 1 a 2 0 − a 3 a 2 ] \begin{bmatrix} a_2a_3 & 0 & -a_1a_2 \\ -a_2a_3 & a_1a_3 & 0\\ 0 & -a_3 & a_2 \\ \end{bmatrix}{\Rightarrow} \begin{bmatrix} a_2a_3 & 0 & -a_1a_2 \\ 0 & a_1a_3 & -a_1a_2\\ 0 & -a_3 & a_2 \\ \end{bmatrix} ⎣⎡a2a3−a2a300a1a3−a3−a1a20a2⎦⎤⇒⎣⎡a2a3000a1a3−a3−a1a2−a1a2a2⎦⎤
第三行乘以 a 1 a_1 a1再加上第二行
[ a 2 a 3 0 − a 1 a 2 0 a 1 a 3 − a 1 a 2 0 − a 1 a 3 a 1 a 2 ] ⇒ [ a 2 a 3 0 − a 1 a 2 0 a 1 a 3 − a 1 a 2 0 0 0 ] \begin{bmatrix} a_2a_3 & 0 & -a_1a_2 \\ 0 & a_1a_3 & -a_1a_2\\ 0 & -a_1a_3 & a_1a_2 \\ \end{bmatrix}{\Rightarrow} \begin{bmatrix} a_2a_3 & 0 & -a_1a_2 \\ 0 & a_1a_3 & -a_1a_2\\ 0 & 0 & 0 \\ \end{bmatrix} ⎣⎡a2a3000a1a3−a1a3−a1a2−a1a2a1a2⎦⎤⇒⎣⎡a2a3000a1a30−a1a2−a1a20⎦⎤
所以3x3的反对称矩阵的秩为2
参考
[1]. 百度百科:反对称矩阵
[2]. share_noel/books/韦穗(译).计算机视觉中的多视图几何,提取码:0ooc
[3]. 北京邮电大学鲁鹏老师计算机视觉课程三维重建部分PPT
[4]. 特征值 是 系数行列式等于0时的 解
完
如有错漏,敬请指正
--------------------------------------------------------------------------------------------诺有缸的高飞鸟202104