详解支持向量机（Support Vector Machines, SVM）

通俗来讲，所谓支持向量机是一种分类器，对于做出标记的两组向量，给出一个最优分割超曲面把这两组向量分割到两边，使得两组向量中离此超平面最近的向量（即所谓支持向量）到此超平面的距离都尽可能远。

一、原始目标

（一）超平面方程

所谓向量，可以简单理解成在直角坐标系中由原点出发，指向某一坐标点的一个剪头，因此它只有两个特征，大小和方向，如下图（以二维空间为例）中$\mathbf{x}$。所谓$n$维超平面（hyperplane）是指在$n$维内积空间中，所有在同一个法向量（如下图中$\mathbf{w}$）上投影长度相同的向量组成的集合，如下图中超平面。

设法向量$\mathbf{w}=[\begin{array}{cccc}{w}_1& w_2& \cdots & w_n\end{array}{]}^T$，其模长为：
$$\Vert \mathbf{w}\Vert =\sqrt{w_1^2+w_2^2+\cdots +w_n^2}$$在上图中记为长度$a$。超平面上的所有向量在法向量方向上的投影长度都相同，记为$l$，即原点到此超平面的距离，所以由内积定义可知，超平面上的任一向量$\mathbf{x}=[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}{]}^T$与此法向量$\mathbf{w}$的内积绝对值就是其在法向量方向投影与法向量模长的乘积，即
$$|{\mathbf{w}}^T\mathbf{x}|=|w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n|=al$$由于一旦法向量和超平面固定，$a$和$l$就都是固定值，所以可将上式中$al$改写成$-b$，并赋予$b>0$的含义是向量$\mathbf{x}$投影方向与超平面在法向量反方向，于是就得到了超平面方程：
$${\mathbf{w}}^T\mathbf{x}+b=0$$并称其中$b$为超平面的截距。
对于超平面外一向量$\mathbf{y}=[\begin{array}{cccc}{y}_1& y_2& \cdots & y_n\end{array}{]}^T$，同理可知该向量与超平面法向量的内积绝对值为：
$$|{\mathbf{w}}^T\mathbf{y}|=|w_1{y}_1+w_2{y}_2+\cdots +w_n{y}_n|=ad$$而在上图中可直观看出向量$\mathbf{y}$到此超平面的距离是$h$，且有如下关系：
$$h=d-l=\frac{ad-al}{a}=\frac{|{\mathbf{w}}^T\mathbf{y}+b|}{\Vert \mathbf{w}\Vert }$$由此可见，超平面外一向量到超平面的几何距离就等于将该向量代入超平面方程取绝对值后，再除以超平面法向量的模长。

（二）严格线性可分问题

设$n$维向量空间中有$m$个向量${\mathbf{x}}_1\sim {\mathbf{x}}_m$，每个向量${\mathbf{x}}_i$都对应一个标签$y_i$，其中一部分向量的标签值是1，另一部分向量的标签值是-1，从而区分出两组向量。我们所要做的是在$n$维向量空间中构造一个超平面 ，使得在超平面两侧找到的支持向量（即距离超平面几何距离最短的向量）${\mathbf{x}}_s$到此超平面的距离尽可能远，由前述超平面方程可知这个距离为：
$$d_s=\frac{|{\mathbf{w}}^T{\mathbf{x}}_s+b|}{\Vert \mathbf{w}\Vert }$$同时要满足同标记的向量只能在此超平面的同一边，即
$$\{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_i+b>0& y_i=1\\ {\mathbf{w}}^T{\mathbf{x}}_i+b<0& y_i=-1\end{array}$$满足上述条件的超平面称为决策面。

二、目标解析

对于上述约束条件，当$y_i=1$时有${\mathbf{w}}^T{\mathbf{x}}_i+b>0$，等价于必然存在$\alpha >0$使得${\mathbf{w}}^T{\mathbf{x}}_i+b>\alpha$；同理，必然存在$-\alpha$使得当$y_i=-1$时，${\mathbf{w}}^T{\mathbf{x}}_i+b<-\alpha$；而由超平面方程可知，$\mathbf{w}$和$b$同比例变化后，方程所描述的仍是同一个超平面，所以上述条件等价于不等式两边同除$\alpha$的结果，即
$$\{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_i+b>1& y_i=1\\ {\mathbf{w}}^T{\mathbf{x}}_i+b<-1& y_i=-1\end{array}$$由于所追求的决策面到其两侧支持向量（${\mathbf{x}}_{s+}$和${\mathbf{x}}_{s-}$）的距离相同，可以令上述$\alpha$就等于支持向量代入决策面表达式后的结果，即
$$\{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_{s+}+b=\alpha & y_{s+}=1\\ {\mathbf{w}}^T{\mathbf{x}}_{s-}+b=-\alpha & y_{s-}=-1\end{array}$$上述条件同样等价于等式两边同除$\alpha$的结果，即
$$\{\begin{array}{ll}{\mathbf{w}}^T{\mathbf{x}}_{s+}+b=1& y_{s+}=1\\ {\mathbf{w}}^T{\mathbf{x}}_{s-}+b=-1& y_{s-}=-1\end{array}$$上述各式等号与不等号两侧再同乘标签值，最终约束条件可简化为:
$$\{\begin{array}{ll}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)>1& i\ne s+或s-\\ y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=1& i=s+或s-\end{array}$$因此，要最大化的目标函数可化为：
$$d_s=\frac{|{\mathbf{w}}^T{\mathbf{x}}_s+b|}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert }$$综上所述，原始目标可以具体描述为如下求条件最值问题：
$$\{\begin{array}{l}\underset{\mathbf{w}}{\max }\frac{1}{\Vert \mathbf{w}\Vert }\\ s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1\\ i=1,2,\cdots ,m\end{array}$$其中$s.t.$是satisfy to的缩写，即同时满足于的意思。

三、兼容软间隔

在实际问题中，总有可能偶尔出现异常数据，比如个别正标向量跑到了负标向量堆里去了，如果严格分类会造成一部分向量与决策面很近，甚至根本无法分界。如下图所示：

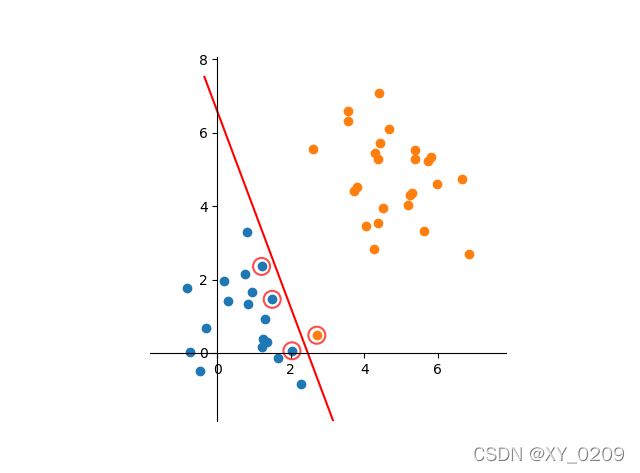
为了容忍个别异常数据，提升模型鲁棒性，实现下图分类效果：

需要对原条件最值问题做调整如下：
$$\{\begin{array}{l}\underset{\mathbf{w}}{\max }\{\frac{1}{\Vert \mathbf{w}\Vert }-C\sum _{i=1}^m{\xi }_i\}\\ s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-{\xi }_i\\ {\xi }_i\ge 0\\ i=1,2,\cdots ,m\end{array}$$其中新增了两个大于0的变量：

1. 松弛变量${\xi }_i$。当${\xi }_i=0$时，说明第$i$个向量要严格遵守分类要求；当$0<{\xi }_i<1$时，说明允许第$i$个向量离决策面的距离比支持向量还近；当${\xi }_i\ge 1$时，表示允许第$i$个向量可以处在决策面上甚至在决策面另一边。
2. 惩罚系数$C$。如果松弛变量的取值不被约束，则相当于此优化问题不再有约束条件了，这样显然不行，因此需要使每个松弛变量都付出代价，即对优化问题产生负面影响，这个影响度就是惩罚系数，该系数越大则越不能容忍例外向量，越小则约能容忍。故而该系数是超参数，即需要人为设定，而非模型训练出来。

四、兼容非线性分割

当出现类似下图的分类问题时，无论如何容忍异常向量，也无法做到在平面上用一条直线分割两类向量。

对于上图中的向量分布，实际上需要一条环线才能有效分割两类向量。以平面上二次曲线为例，其方程形式为：
$$w_0+w_1{x}_1+w_2{x}_2+w_3{x}_1^2+w_4{x}_2^2+w_5{x}_1{x}_2=0$$就相当于将原二维向量映射到五维空间后的线性方程，即
$${\mathbf{w}}^T\varphi (\mathbf{x})+b=0$$其中
$$\varphi (\mathbf{x})=\left[\begin{array}{c}{x}_1\\ x_2\\ x_1^2\\ x_2^2\\ x_1{x}_2\end{array}\right],\mathbf{w}=\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\\ w_4\\ w_5\end{array}\right],b=w_0$$由此可见，在低维空间无法线性分割的两组向量可以映射到高维空间实现线性分割。为兼容非线性分割问题，需要再次对上述条件最值问题做调整，得到最终目标如下：
$$\{\begin{array}{l}\underset{\mathbf{w}}{\max }\{\frac{1}{\Vert \mathbf{w}\Vert }-C\sum _{i=1}^m{\xi }_i\}\\ s.t.y_i[{\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b]\ge 1-{\xi }_i\\ {\xi }_i\ge 0\\ i=1,2,\cdots ,m\end{array}$$至此，终于将既兼容软间隔，又兼容非线性分割的SVM模型描述成了条件最值问题。后面就是如何求解此条件最值问题了。

五、拉格朗日乘数法

为便于构造拉格朗日函数后计算梯度，可将原条件最值问题等价为：
$$\{\begin{array}{l}\underset{\mathbf{w}}{\min }\{\frac{\Vert \mathbf{w}{\Vert }^2}{2}+C\sum _{i=1}^m{\xi }_i\}\\ s.t.1-{\xi }_i-y_i[{\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b]\le 0\\ {\xi }_i\ge 0\\ i=1,2,\cdots ,m\end{array}$$拉格朗日函数的作用是可以把所有约束条件囊括进一个多元函数，通过求该多元函数的最值来得到想要的条件最值。具体原理证明不在此文中详述，我们只需知道所谓拉格朗日函数就是将所有以小于零作为条件的各条件函数分别乘上一个系数，再加上要求最小值的目标函数后组成的多项式。针对上述条件最值问题，可构造拉格朗日函数如下：
$$L(\mathbf{w},\mathbf{\xi },b,\mathbf{a},\mathbf{\mu })=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{a}_i\{1-{\xi }_i-y_i[{\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b]\}-\sum _{i=1}^m{\mu }_i{\xi }_i$$由于优化的目标是求条件最小值，而约束条件又是一系列不等式，如果直接对上述$L$函数取梯度为零点，则相当于在约束边界上找最小值，但我们想要的效果是最小值只要在约束区域内就行，不一定只能在边界上。也就是说通过$L$函数中$(\mathbf{w},\mathbf{\xi },b)$变量（即除去约束条件前的系数变量）求得的最小值位置可能落在约束区域内也可能落在外面，对于这两种情况，我们想要的效果是：

1. 如果恰好就落在哪几个约束区域内，则这几个约束条件就可以无视了，即其前面的条件系数就可以为0；
2. 如果落在哪几个约束区域外，则这几个约束条件就要起作用，把取值点限定在只能在该条件边界上。

要实现上述目的，我们只需要先在限定条件系数（即$\mathbf{a}$和$\mathbf{\mu }$）大于0的同时由这些条件系数求$L$函数最大值后，再通过非条件系数变量$(\mathbf{w},\mathbf{\xi },b)$求$L$函数最小值即可。因为约束条件都是约束小于0的，所以

1. 一旦某个约束条件被满足了，则该条件项就变成负数了，此时要想让$L$函数值尽可能大，则该条件项前的条件系数就只能变成0，这样第一个想要的效果就满足了；
2. 一旦某个约束条件没被满足，则该条件项就变成正数了，此时要想让$L$函数值尽可能大，则该条件项前的条件系数就会尽可能大，甚至到正无穷。而后续还会对$L$函数取最小值，这样就使得这些项前系数取到正无穷的条件项只能取0，即把取值点限定在该条件边界上，从而也满足了第二个想要的效果。

因此，最终的目标可描述为：
$$\underset{\mathbf{w},\mathbf{\xi },b}{\min }\underset{\mathbf{a}\ge 0,\mathbf{\mu }\ge 0}{\max }L(\mathbf{w},\mathbf{\xi },b,\mathbf{a},\mathbf{\mu })$$由于取最大结果中的最小值和取最小结果中的最大值效果相同（即拉格朗日对偶性），因此上述问题又等价于:
$$\underset{\mathbf{a}\ge 0,\mathbf{\mu }\ge 0}{\max }\underset{\mathbf{w},\mathbf{\xi },b}{\min }L(\mathbf{w},\mathbf{\xi },b,\mathbf{a},\mathbf{\mu })$$第一步先取最小值，通过使$L$函数分别对各自变量的偏导为零可得，即
$${\nabla }_{\mathbf{w},\mathbf{\xi },b}L=\{\begin{array}{l}\frac{\partial L}{\partial \mathbf{w}}=\mathbf{w}-\sum _{i=1}^m{a}_i{y}_i\varphi ({\mathbf{x}}_i)=0\\ \frac{\partial L}{\partial b}=-\sum _{i=1}^m{a}_i{y}_i=0\\ \frac{\partial L}{\partial {\xi }_i}=C-a_i-{\mu }_i=0\end{array}$$将上述结论代入第一步优化目标得
$$\begin{array}{rl}\underset{\mathbf{w},\mathbf{\xi },b}{\min }L(\mathbf{w},\mathbf{\xi },b,\mathbf{a},\mathbf{\mu })& =\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{a}_i\{1-{\xi }_i-y_i[{\mathbf{w}}^T\varphi ({\mathbf{x}}_i)+b]\}-\sum _{i=1}^m{\mu }_i{\xi }_i\\ & =\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{a}_i-\sum _{i=1}^m{a}_i{\xi }_i-{\mathbf{w}}^T\mathbf{w}-b\sum _{i=1}^m{a}_i{y}_i-C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^m{a}_i{\xi }_i\\ & =\sum _{i=1}^m{a}_i-\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\\ & =\sum _{i=1}^m{a}_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{a}_i{a}_j{y}_i{y}_j\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)\end{array}$$第二步就是进一步求解$\underset{\mathbf{a}\ge 0,\mathbf{\mu }\ge 0}{\max }\underset{\mathbf{w},\mathbf{\xi },b}{\min }L(\mathbf{w},\mathbf{\xi },b,\mathbf{a},\mathbf{\mu })$，结合上述条件，原条件最值问题可化为如下优化问题：
$$\{\begin{array}{l}\underset{\mathbf{a}}{\min }\{\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{a}_i{a}_j{y}_i{y}_j\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)-\sum _{i=1}^m{a}_i\}\\ s.t.\sum _{i=1}^m{a}_i{y}_i=0\\ a_i,{\mu }_i\ge 0\\ C-a_i-{\mu }_i=0\\ i=1,2,\cdots ,m\end{array}$$由于
$$\{\begin{array}{l}{\mu }_i\ge 0\\ {\mu }_i=C-a_i\end{array}\Rightarrow a_i\le C$$从而得到最终条件最值问题：
$$\{\begin{array}{l}\underset{\mathbf{a}}{\min }\{\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{a}_i{a}_j{y}_i{y}_j\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)-\sum _{i=1}^m{a}_i\}\\ s.t.\sum _{i=1}^m{a}_i{y}_i=0\\ 0\le a_i\le C\\ i=1,2,\cdots ,m\end{array}$$上述问题涉及映射到高维空间的向量内积，即$\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)$的计算问题，需要引入核函数。

六、核函数

在第四章的例子中，对二维向量做二次曲线分割就需要映射到五维空间，如果三维甚至更高维度向量做高次超曲面分割，所要升的维度将很高，从而造成极大的计算量。因此需找到一种方法，使得两个低维向量无需向高维空间做映射，只需在原维度空间做简单运算，所得结果就等于其映射到高维空间后的内积。这种方法就是核函数，将同是低维度的两个向量代入核函数，所得结果就是其映射到高维空间后的内积，即
$$\varphi ({\mathbf{x}}_i{)}^T\varphi ({\mathbf{x}}_j)=\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$$常用的核函数有以下几种：
1、线性核。就表示原空间内积，适用于线性可分问题。
$$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)={\mathbf{x}}_i^T{\mathbf{x}}_j$$2、高斯核。适用于没有先验经验的非线性分类。其中$\sigma$越小，使得映射的维度越高。
$$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=\exp \left(-\frac{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2}{2{\sigma }^2}\right)$$3、多项式核。适用于没有先验经验的分类。其中$d$越越小，使得映射的维度越高。
$$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=(a{\mathbf{x}}_i^T{\mathbf{x}}_j+c{)}^d$$4、Sigmoid核。此时SVM实现的就是一种多层感知器神经网络。
$$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=\tanh (a{\mathbf{x}}_i^T{\mathbf{x}}_j+c)$$
大多数非线性分割使用高斯核都能很好处理。

七、SMO算法

通过核函数解决了高维向量内积计算问题后，就剩下如何求解出满足约束条件的一组最优条件系数$\mathbf{a}$这最后一个问题了。由于条件系数$a_i$的个数与待分割向量一样多，难以直接计算梯度最低点，故而采用SMO算法，即序列最小优化（Sequential Minimal Optimization）算法。其思路是每次选择两个待优化条件系数而固定其他系数，由约束条件又可以化去一个系数，从而化成一个一元二次函数的求最值问题。对于已满足约束条件的最优解，再使用SMO算法做迭代优化时，是不会改变其结果的，所以当通过两两优化的方式把所有条件系数遍历几遍，各系数已不再有可优化空间后，即得到了最优结果。

（一）无约束最小化

首先选定$a_1$和$a_2$做优化，其他系数由于都先被视为常量，所以可以都先无视；并用核函数代替映射到高维空间的向量内积，则前述条件最值问题可化为：
$$\{\begin{array}{l}\underset{\mathbf{a}}{\min }\{\frac{1}{2}{a}_1^2\kappa ({\mathbf{x}}_1,{\mathbf{x}}_1)+\frac{1}{2}{a}_2^2\kappa ({\mathbf{x}}_2,{\mathbf{x}}_2)+y_1{y}_2{a}_1{a}_2\kappa ({\mathbf{x}}_1,{\mathbf{x}}_2)+y_1{a}_1\sum _{i=3}^m{y}_i{a}_i\kappa ({\mathbf{x}}_i,{\mathbf{x}}_1)+y_2{a}_2\sum _{i=3}^m{y}_i{a}_i\kappa ({\mathbf{x}}_i,{\mathbf{x}}_2)-(a_1+a_2)\}\\ s.t.a_1{y}_1+a_2{y}_2=-\sum _{i=3}^m{a}_i{y}_i=\varsigma \\ 0\le a_i\le C\\ i=1,2,\cdots ,m\end{array}$$其中$\varsigma$为常数；$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$可简记为${\kappa }_{ij}$。由此，上述要最小化的目标函数可记为：
$$J=\frac{1}{2}{a}_1^2{\kappa }_{11}+\frac{1}{2}{a}_2^2{\kappa }_{22}+y_1{y}_2{a}_1{a}_2{\kappa }_{12}+y_1{a}_1\sum _{i=3}^m{y}_i{a}_i{\kappa }_{i1}+y_2{a}_2\sum _{i=3}^m{y}_i{a}_i{\kappa }_{i2}-(a_1+a_2)$$由于$a_1{y}_1+a_2{y}_2=\varsigma$，且$y_i$只可能取$\pm 1$，可得$a_1=y_1(\varsigma -a_2{y}_2)$，代入上式对$a_2$求偏导为：
$$\frac{\partial J}{\partial a_2}=({\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12})a_2+(y_2{\kappa }_{12}-y_2{\kappa }_{11})\varsigma -y_2\sum _{i=3}^m{y}_i{a}_i{\kappa }_{i1}+y_2\sum _{i=3}^m{y}_i{a}_i{\kappa }_{i2}+y_1{y}_2-1$$令上式等于0，同时将待优化更新的$a_2$记为$a_2^{\prime }$，区别于其他仍未更新的旧值$a_i$，有：
$$({\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12})a_2^{\prime }=(y_2{\kappa }_{11}-y_2{\kappa }_{12})\varsigma +y_2\sum _{i=3}^m{y}_i{a}_i{\kappa }_{i1}-y_2\sum _{i=3}^m{y}_i{a}_i{\kappa }_{i2}-y_1{y}_2+1$$由于
$$\sum _{i=1}^m{y}_i{a}_i{\kappa }_{ij}=a_1{y}_1{\kappa }_{1j}+a_2{y}_2{\kappa }_{2j}+\sum _{i=3}^m{y}_i{a}_i{\kappa }_{ij}$$代入上式可得：
$$\begin{array}{rl}({\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12})a_2^{\prime }& =(y_2{\kappa }_{11}-y_2{\kappa }_{12})\varsigma +y_2(\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i1}-a_1{y}_1{\kappa }_{11}-a_2{y}_2{\kappa }_{21})-y_2(\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i2}-a_1{y}_1{\kappa }_{12}-a_2{y}_2{\kappa }_{22})-y_1{y}_2+1\\ & =(y_2{\kappa }_{11}-y_2{\kappa }_{12})\varsigma +y_2\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i1}-y_1{y}_2{a}_1{\kappa }_{11}-a_2{\kappa }_{21}-y_2\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i2}+y_1{y}_2{a}_1{\kappa }_{12}+a_2{\kappa }_{22}-y_1{y}_2+1\end{array}$$为简化表达式，记
$$E_j=\sum _{i=1}^m{y}_i{a}_i{\kappa }_{ij}-y_j$$即
$$\mathbf{E}=\left[\begin{array}{c}{E}_1\\ E_2\\ ⋮\\ E_m\end{array}\right]=\left[\begin{array}{c}\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i1}-y_1\\ \sum _{i=1}^m{y}_i{a}_i{\kappa }_{i2}-y_2\\ ⋮\\ \sum _{i=1}^m{y}_i{a}_i{\kappa }_{im}-y_m\end{array}\right]=\left[\begin{array}{cccc}{\kappa }_{11}& {\kappa }_{12}& \cdots & {\kappa }_{1m}\\ {\kappa }_{21}& {\kappa }_{22}& \cdots & {\kappa }_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ {\kappa }_{m1}& {\kappa }_{m2}& \cdots & {\kappa }_{mm}\end{array}\right]\left[\begin{array}{c}{y}_1{a}_1\\ y_2{a}_2\\ ⋮\\ y_m{a}_m\end{array}\right]-\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$$则有：
$$y_2(E_1-E2）=y_2\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i1}-y_1{y}_2-y_2\sum _{i=1}^m{y}_i{a}_i{\kappa }_{i2}+1$$代入前式可化简为：
$$({\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12})a_2^{\prime }=(y_2{\kappa }_{11}-y_2{\kappa }_{12})\varsigma -y_1{y}_2{a}_1{\kappa }_{11}-a_2{\kappa }_{21}+y_1{y}_2{a}_1{\kappa }_{12}+a_2{\kappa }_{22}+y_2(E_1-E_2)$$再将$a_1=y_1(\varsigma -a_2{y}_2)$代入上式可得：
$$\begin{array}{rl}({\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12})a_2^{\prime }& =y_2{\kappa }_{11}\varsigma -y_2{\kappa }_{12}\varsigma -y_2(\varsigma -a_2{y}_2){\kappa }_{11}-a_2{\kappa }_{21}+y_2(\varsigma -a_2{y}_2){\kappa }_{12}+a_2{\kappa }_{22}+y_2(E_1-E_2)\\ & =a_2{\kappa }_{11}-a_2{\kappa }_{21}-a_2{\kappa }_{12}+a_2{\kappa }_{22}+y_2(E_1-E_2)\\ & =({\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12})a_2+y_2(E_1-E_2)\end{array}$$因此：
$$a_2^{\prime }=a_2+y_2\frac{E_1-E_2}{{\kappa }_{11}+{\kappa }_{22}-2{\kappa }_{12}}$$上式右侧$a_2$是未更新的旧值。此时得到的$a_2^{\prime }$还并没有考虑约束条件$0\le a_i\le C$ ，因此还有待修剪。为方便区分，最终修剪后的各条件系数记为${\hat{a}}_i$

（二）根据约束条件做修剪

结合约束条件$0\le a_i\le C$及$a_1{y}_1+a_2{y}_2=\varsigma$，可确定$({\hat{a}}_1,{\hat{a}}_2)$的坐标只能落在下图方框中：

由$y_1$和$y_2$的不同取值可分四种情况讨论：

1. 当$y_1=y_2=1$时，有${\hat{a}}_2=-{\hat{a}}_1+\varsigma$。此时$\varsigma \ge 0$，如上面左图所示，区分$\varsigma$与$C$的位置关系做分类讨论如下：
   （1）当$0\le \varsigma \le C$时，${\hat{a}}_1\in [0,\varsigma ]$，所以${\hat{a}}_2\in [0,\varsigma =a_1+a_2]$。
   （2）当$C\le \varsigma \le 2C$时，${\hat{a}}_1\in [\varsigma -C,C]$，所以${\hat{a}}_2\in [\varsigma -C=a_1+a_2-C,C]$。
2. 当$y_1=y_2=-1$时，有${\hat{a}}_2=-{\hat{a}}_1-\varsigma$。此时$\varsigma \le 0$，将此处取负值的$\varsigma$换成上述取正值的$\varsigma$，可得与上述相同的结果。
3. 当$y_1=1$，$y_2=-1$时，有${\hat{a}}_2={\hat{a}}_1-\varsigma$。此时$-C\le \varsigma \le C$，如上面右图所示，区分$\varsigma$与$0$的位置关系做分类讨论如下：
   （1）当$-C\le \varsigma \le 0$时，${\hat{a}}_1\in [0,C+\varsigma ]$，所以${\hat{a}}_2\in [-\varsigma =a_2-a_1,C]$。
   （2）当$0\le \varsigma \le C$时，${\hat{a}}_1\in [\varsigma ,C]$，所以${\hat{a}}_2\in [0,C-\varsigma =C+a_2-a_1]$。
4. 当$y_1=-1$，$y_2=1$时，有${\hat{a}}_2={\hat{a}}_1+\varsigma$。同理可将此处$\varsigma$换成$-\varsigma$，可得与上述相同的结果。

综上可得${\hat{a}}_2$的取值上下界为：
$$\{\begin{array}{ll}if(y_1=y_2)L=\max \{0,a_1+a_2-C\}& H=\min \{a_1+a_2,C\}\\ if(y_1\ne y_2)L=\max \{a_2-a_1,0\}& H=\min \{C,C+a_2-a_1\}\end{array}$$注意，上述$a_1$和$a_2$都是指本轮更新前的原值。至此可得：
$$\begin{array}{rl}{\hat{a}}_2& =\{\begin{array}{ll}H& a_2^{\prime }>H\\ a_2^{\prime }& L\le a_2^{\prime }\le H\\ L& a_2^{\prime }<H\end{array}\\ {\hat{a}}_1& =y_1(\varsigma -{\hat{a}}_2{y}_2)=y_1[(y_1{a}_1+y_2{a}_2)-{\hat{a}}_2{y}_2]=a_1+y_1{y}_2(a_2-{\hat{a}}_2)\end{array}$$以此类推，将所有条件系数$a_i$遍历更新几遍后即得到最终优化后的一组条件系数${\hat{a}}_i$。

由第五章可知，在拉格朗日函数中，对于不等式约束条件项，要么该约束条件表达式取0，要么该条件项前的条件系数取0（即所谓KKT条件），即若${\hat{a}}_s\ne 0$，则$y_s(\sum _{i=1}^m{a}_i{y}_i{\kappa }_{is}+b)\ge 1-{\xi }_s$，也就是说该${\mathbf{x}}_s$向量要么是支持向量，即${\xi }_s=0$；要么就是被容忍的异常向量，即${\xi }_s>0$。对于支持向量，有
$$b=y_s-\sum _{i=1}^m{a}_i{y}_i{\kappa }_{is}=-E_s$$所以我们只需找到支持向量就可求得决策面截距。同时上式也说明凡支持向量，其对应的偏移量$E$都是相等的，所以我们只需要找到所有条件系数不为零的特殊向量，再从这些特殊向量所对应的偏移量中找到出现次数最多的值，就是支持向量的偏移量，再取负数就得到了决策面的截距$\hat{b}$。最终得到决策面方程为：
$$\sum _{i=1}^m{\hat{a}}_i{y}_i\kappa ({\mathbf{x}}_i,\mathbf{x})+\hat{b}=0$$

八、应用示例

（一）SVM函数代码

import numpy as np
import numpy.matlib as matlib
import numpy.random as random
from collections import Counter

# 定义高斯核函数
def gaussKernel(X, Y, sigma=3):
    '''
    Parameters
    ----------
    X : np.matrix
        一个n行m列矩阵，代表m个n维向量。
    Y : np.matrix
        一个n行m列矩阵，代表另外m个n维向量。
    sigma : float
        调控参数。越小映射的空间维度约高。默认为3。

    Returns
    -------
    K : np.matrix
        一个m行1列矩阵，其中k_i = exp[-(||X_i-Y_i||^2)/(2*sigma^2)]。
    
    Examples
    --------
    X = np.matrix('1, 2, 3; 4, 5, 6').T 
    Y = np.matrix('1, 3, 5; 2, 4, 6').T
    K = gaussKernel(X, Y, 3)
    '''
    K = np.exp(-(np.square(X - Y).T * matlib.ones((np.shape(X)[0], 1))) / (2*sigma**2))
    return K

# 基于SVM对一组做了二元标记的向量给出划分界限的决策平面
def svnSimple(dataMatrix, labelVector, C, maxIter, kernel=None, sigma=3):
    '''
    Parameters
    ----------
    dataMatrix : np.matrix
        一个n行m列矩阵，代表m个n维向量，作为待分类向量。
    labelVector : np.matrix
        一个由+1和-1组成的1行m列矩矩阵，作为dataMatrix各列向量的标签。
    C : float
        惩罚系数。一个大于等于0的数值，越接近0则对异常向量的容忍度越高。
    maxIter : int
        最大遍历次数。对所有条件系数做一次迭代更新为一次遍历。
    kernel : function
        核函数。用于在低维空间计算映射到高维空间的向量内积。
    sigma : float
        核函数的调控参数。越小映射的空间维度约高。默认为3。

    Returns
    -------
    A : np.matrix
        一个1行m列矩阵，代表最优条件系数向量。
    b : float
        一个1行1列矩阵，代表决策平面的截距。
    
    Examples
    --------
    X = np.matrix('1, 1; 4, 3; 3, 3').T 
    Y = np.matrix('-1, 1, 1')
    A, b = svnSimple(X, Y, 100, 10)
    '''
    n, m = np.shape(dataMatrix)         # 初始化待分向量维度和向量个数
    A = matlib.zeros((1, m))            # 初始化条件系数向量
    
    # 初始化待分向量间内积矩阵
    if callable(kernel):                # 如果给定了核函数则使用核函数做高维内积
        K = matlib.zeros((m, m))        # 初始化高维内积矩阵
        for i in range(m):
            K[:,i] = kernel(dataMatrix[:,i] * matlib.ones((1,m)), dataMatrix, sigma)
    else:
        K = dataMatrix.T * dataMatrix

    # 由SMO算法迭代出所有最优条件系数
    iterNum = 0                         # 初始化迭代次数
    effTraversalNum = 0                 # 初始化有效遍历次数
    while (iterNum < maxIter):
        alphaPairsChanged = 0           # 初始化条件系数更新次数
        for i in range(m):
            # 计算各待分向量到决策面的偏移值（不含b影响）向量
            E = (K*np.multiply(A, labelVector).T ).T- labelVector
            # 从其他条件系数中再随机选出一个与当前条件系数作为一对待优化系数
            j = i
            while (j == i):
                j = int(random.uniform(0, m))
            # 计算当前待优化的第二个条件系数a2的待修剪值
            a2 = A[0,j] + labelVector[0,j]*(E[0,i]-E[0,j])/(K[i,i]+K[j,j]-2*K[i,j])
            # 计算a2的上下界
            if labelVector[0,i] == labelVector[0,j]:
                l = max(0, A[0,i]+A[0,j]-C)
                h = min(C, A[0,i]+A[0,j])
            else:
                l = max(0, A[0,j]-A[0,i])
                h = min(C, C+A[0,j]-A[0,i])
            # 修剪条件系数a2
            if a2 > h:
                a2 = h
            elif a2 < l:
                a2 = l
            # 当a2更新变化太小时便无需更新
            if (abs(A[0,j] - a2) < 0.00001): continue
            # 计算条件系数a1
            a1 = A[0,i] + labelVector[0,i]*labelVector[0,j]*(A[0,j]-a2)
            # 更新条件系数向量
            A[0,i] = a1
            A[0,j] = a2
            # 统计本此遍历中条件系数更新次数
            alphaPairsChanged += 1
        # 统计有效遍历次数
        if alphaPairsChanged != 0: effTraversalNum += 1
        # 遍历迭代次数加1
        iterNum += 1
    print("共完成有效遍历%d次。" %effTraversalNum)
    
    # 通过支持向量计算决策平面截距b
    spVecIndex = []                            # 初始化特殊向量序号集合
    for k in range(m):
        if abs(A[0,k]) > 0.01:                 # 条件系数显著大于零对应的是特殊向量
            spVecIndex.append(k)
    spE = E[:, spVecIndex].tolist()[0]         # 获取所有特殊向量偏移值
    roundSpE = []                      
    for n in spE: roundSpE.append(round(n, 4)) # 精确到小数点后4位
    # 对各偏移量按出现次数由大到小排序
    listRoundSpE = list(Counter(roundSpE).items())
    listRoundSpE.sort(key=lambda x:x[1],reverse=True)
    b = -listRoundSpE[0][0]                    # 出现次数最多的E对应支持向量
    return A, b

（二）绘图代码

import numpy as np
import numpy.matlib as matlib
import matplotlib.pyplot as plt

# 绘制待分二维向量散点图及其分界线（如有）
def showDataSet(dataMatrix, labelVector, A=None, b=None, kernel=None, sigma=None):
    '''
    Parameters
    ----------
    dataMatrix : np.matrix
        一个2行m列矩阵，代表m个2维向量，作为待分类向量。默认第一行是横坐标，第二行是纵坐标。
    labelVector : np.matrix
        一个由+1和-1组成的1行m列矩矩阵，作为dataMatrix各列向量的标签。
    A : np.matrix
        一个1行m列矩阵，代表各待分向量对应的条件系数，非零系数对应支持向量。默认为空，
        即不画分界线。
    b : float
        一个1行1列矩阵，代表决策平面的截距。默认为空，即不绘制分界线。
    kernel : function
        核函数。用于在低维空间计算映射到高维空间的向量内积。为空则默认为原向量空间内积。
    sigma : float
        核函数的调控参数。越小映射的空间维度约高。

    Returns
    -------
    null
    
    Notes
    -----
    只能绘制二维向量散点图。
    
    Examples
    --------
    X = np.matrix('1, 1; 4, 3; 3, 3').T 
    Y = np.matrix('-1, 1, 1')
    A = np.matrix('0.25, 0, 0.25')
    b = np.matrix('-2')
    showDataSet(X, Y, A, b)
    '''
    n, m = np.shape(dataMatrix)               # 初始化待分向量维度和向量个数
    if not n == 2:                            # 校验向量维度只能是2维
            raise Exception("only 2-dimension vectors can be darwn")
    plusColumNum = []                         # 正向量列号集合
    minusColumNum = []                        # 负向量列号集合
    for i in range(m):
        if labelVector[0,i] > 0:              # 如果标签为正
            plusColumNum.append(i)            # 将列号归入正向量列集合
        else:
            minusColumNum.append(i)           # 否则将列号归入负向量列集合
    plusData = dataMatrix[:, plusColumNum]    # 由正向量列号获取组成正向量矩阵
    minusData = dataMatrix[:, minusColumNum]  # 由负向量列号获取组成负向量矩阵
    plt.figure()
    plt.axis('scaled')                        # 横纵坐标尺度一致（即使在窗口缩放时）
    x_min = min(min(dataMatrix[0].tolist()[0])-1, 0)  # X轴下限
    x_max = max(max(dataMatrix[0].tolist()[0])+1, 0)  # X轴上限
    y_min = min(min(dataMatrix[1].tolist()[0])-1, 0)  # Y轴下限
    y_max = max(max(dataMatrix[1].tolist()[0])+1, 0)  # Y轴上限
    plt.xlim([x_min, x_max])                  # 设置x轴坐标系范围
    plt.ylim([y_min, y_max])                  # 设置y轴坐标系范围
    plt.scatter(plusData[0].tolist()[0], plusData[1].tolist()[0])   #正向量散点图
    plt.scatter(minusData[0].tolist()[0], minusData[1].tolist()[0]) #负向量散点图
    # 移动坐标系
    ax = plt.gca()                               # 获取当前坐标系
    ax.spines['right'].set_color('none')         # 右边框设置成无颜色
    ax.spines['top'].set_color('none')           # 上边框设置成无颜色 
    ax.spines['bottom'].set_position(('data',0)) # x轴在y轴，０的位置
    ax.spines['left'].set_position(('data',0))   # y轴在x轴，０的位置
    # 绘制分界线
    if b is not None:                            # 如果条件系数向量非空
        x = np.linspace(x_min, x_max, 100)
        y = np.linspace(y_min, y_max, 100)
        meshX,meshY = np.meshgrid(x,y)           # 对向量显示区域网格化
        vecX = matlib.zeros((2, 1))              #