数据挖掘 / 机器学习——决策树

《数据挖掘》国防科技大学
《数据挖掘》青岛大学
《机器学习》周志华
《统计学习方法》李航

数据挖掘/机器学习之决策树

一、概述

决策树(Decision Tree)是从一组无次序、无规则，但有类别标号的样本集中推导出的、树形表示的分类规则。

如何选择测试属性：测试属性的选择顺序影响决策树的结构甚至决策树的准确率。
如何停止划分样本：从根结点测试属性开始，每个内部结点测试属性都把样本空间划分为若干个子区域，一般当某个子区域的样本同属一个类别时，就停止划分样本。有时也通过设置特定条件来停止划分样本，例如树的深度达到用户指定的深度，结点中样本的个数少于用户指定的个数等。

1. 任务属性

分类任务、回归任务(CART)

2. 结构

根结点：样本全集
内部结点：表示一个特征或属性
叶结点：表示一个类
根到叶的路径：表示分类规则

3. 特点

• 决策树分类方法采用自顶向下的递归方式

• 树状结构，可以很好的对数据进行分类；

• 决策树的根节点到叶节点的每一条路径构建一条规则，整棵决策树就对应着一组析取表达式规则；

• 具有互斥且完备的特点，即每一个样本均被且只能被一条路径所覆盖；

• 只要提供的数据量足够庞大真实，通过数据挖掘模式，就可以构造决策树。

• 优点
  ➢ 易理解：决策规则建立的过程易理解
  ➢ 可视化：树形结构可以可视化，直观
  ➢ 效率高：决策树只需一次构建，反复使用
  ➢ 在学习过程中不需要使用者了解很多背景知识。

• 缺点
  ➢ 过拟合：容易生成复杂的树结构（剪枝可以缓解过拟合的负作用）
  ➢ 泛化能力差：基于贪心算法建立，不能保证建立全局最优的决策树 （随机森林算法 进行优化）

4. 基本算法

Hunt算法是Hunt等人1966年提出的决策树算法，它在选择划分训练集的属性时采用贪心策略，将训练集相继划分成较纯(包括更少类别)的子集，以递归方式建立决策树，并成为许多决策树算法的衍生框架，包括ID3、C4.5等。
Hunt算法框架：
假设结点h对应的样本集用S_h表示，而C={C₁, C₂, …, C_k}是其类别属性
Hunt算法的递归定义如下：
(1) 如果S_h中所有样本点都属于同一个类C_h，则h为叶结点，并用分类标号Ch标记该结点。
(2) 如果S_h中包含多个类别的样本点，选择一个“好”的属性A，以属性A命名h并作为一个内部结点；然后按属性A的取值将S_h划分为较小的子集，并为每个子集创建A的子女结点；然后把A的每个子女结点作为h结点，递归地调用Hunt算法。
Hunt算法的停止策略：
(1)简单策略：分裂结点直到所有的记录都属于同一个类，或者所有的记录都具有相同的属性值。
(2)其它策略：在实际过程中还可能出现其它情况，应该考虑其它的标准来提前终止决策树的生长过程。比如附加条件：
① 子女结点为空
在hunt算法第(2)步所创建的子女结点可能为空，即不存在与这些结点条件相关联的样本点，则仍将该结点设为叶结点，其类别标号采用其父结点上多数样本的类别标号。
② 训练集S_h的候选属性集合为空，但类别标号却不相同，仍将该结点设置为叶结点，其类别标号采用该结点多数样本的类别标号。

5. 生成过程

决策树分类模型的建立通常分为两个步骤：
– 决策树生成
– 决策树修剪。
决策树的生成是一个递归过程。有三种情形会导致递归返回：
① 当前结点包含的样本全属于同一类别，无需划分；
② 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；【把当前结点标记为叶结点，将其类别设定为该结点包含样本最多的类别-利用当前结点的后验分布】
③ 当前结点包含的样本集合为空，不能划分。【把当前结点标记为叶结点，但将其类别设定为其父节点所含样本最多的类别-把父节点的样本分布作为当前结点的先验分布】

决策树生成算法

决策树修剪算法

基本的决策树构造算法没有考虑噪声，因此生成的决策树完全与训练例子拟合。在有噪声情况下，将导致过分拟合（Overfitting），即对训练数据的完全拟合反而使对现实数据的分类预测性能下降。剪枝是一种克服噪声的基本技术，同时它也能使树得到简化而变得更容易理解。
• 两种基本的剪枝策略：

• 预先剪枝（Pre-Pruning）：在生成树的同时决定是继续对不纯的训练子集进行划分还是停机。（如果划分带来的信息增益、Gini指标等低于阈值，或元组数目低于阈值，则停止这次划分）
• 后剪枝（Post-Pruning）：首先生成与训练数据完全拟合的一棵决策树，然后从树的叶子开始剪枝，逐步向根的方向剪。剪枝时要用到一个测试数据集。如果存在某个叶子剪去后能使得在测试集上的准确度或其他测度不降低（不变得更坏），则剪去该叶子；否则停机。
  • 要防止过分剪枝（Over-Pruning）带来的副作用。
  

二、决策划分

1. 意义

如何选择最优划分属性是决策树学习的关键

2. 期望

决策树的分支节点所包含的样本尽可能地属于同一类，即结点的“纯度”越来越高。

3. 信息熵

信息熵/量 (information entropy)：用于度量样本集合纯度的最常用的指标。熵值越高，数据越混乱；熵值越低，数据越纯。

p_i (i = 1, 2,. . . , ICI) 为当前样本集合S中第i类样本所占的比例。

Ent(S) 的值越高，则S的纯度越高。

4. 三个划分属性的准则

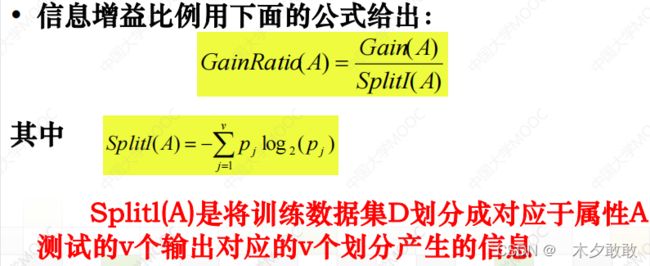
（1）信息增益（information gain）

用属性A对样本集S进行划分所获得的信息增益：

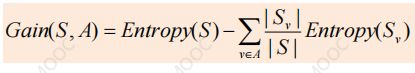
Sv: the subset of S where attribute A takes the value v.

（2）增益率 （gain ratio）

（3）基尼指数（Gini index）

三、ID3算法

◼ ID3算法是一个从上到下、分而治之的归纳过程。
◼ 计算每个属性的信息增益，每次划分选取信息增益最高的属性为划分标准，由该属性的不同取值建立分支
◼ 再对各分支的子集递归调用该方法建立决策树节点的分支，直至生成一个能完美分类训练样例的决策树。

1. 数据要求：

• 所有属性必须为离散属性
• 所有训练实例必须有一个明确的分类。

2. 基本策略：

• 决策树开始时，根节点包含所有训练样本
• 若一个节点的样本均为同一类别，则该节点就成为叶节点并标记为该类别。
• 否则算法采用信息增益作为选择标准来帮助选择合适的（分支）属性，信息增益最大的属性成为该节点的“测试”/“判定”属性。
• 对测试属性的每个已知的值，创建一个分支，并据此划分样本
• 算法使用同样的过程，从剩余属性中选择，递归的形成每个分支划分上的样本决策树。

3.优缺点

• 优点：
   算法理论清晰，方法简单，学习能力较强。
   分类速度较快。
• 缺点
   只能处理离散属性数据
   不能处理有缺失的数据
   仅是局部最优的决策树
   偏好取值种类多的属性

四、C4.5算法

C4.5算法是从ID3算法演变而来，除了拥有ID3算法的功能外，C4.5算法引入了新的方法、增加了新的功能：

• 用信息增益比例的概念；
• 可以处理具有缺少属性值的训练样本；
• 通过使用不同的修剪技术以避免树的过度拟合；
• K交叉验证等。

C4.5处理连续值的属性

C4.5处理空值

(1) 删除训练集中有空值的样本
(2) 以某种方法填充缺失数据，其中：
➢ 数值属性：用该属性非空值的平均值或频率最高值去填充
➢ 离散属性：用该属性出现频率最高的值去填充空值，或将空值作为一种特殊取值对待等。

五、CART

分类与回归树(classification and regression tree, CART)模型由Breiman等人在1984年提出，是应用广泛的决策树学习方法。CART同样由特征选择、树的生成及剪枝组成，既可以用于分类也可以用于回归。以下将用于分类与回归的树统称为决策树。

1. 算法思想

CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征，将输入空间即特征空间划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。

2. 步骤

(1)决策树生成:基于训练数据集生成决策树，生成的决策树要尽量大;
(2)决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

决策树生成

决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。


算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的基尼指数小于预定阈值(样本基本属于同一类)，或者没有更多特征。

决策树剪枝

CART剪枝算法从“完全”生长的决策树的底端剪去一些子树，使决策树变小，即模型变简单，从而能够对未知数据有更准确的预测。

预测误差，如基尼指数

六、为不同类型的属性指定测试条件

基于标称属性的分裂

多路划分：划分数（输出数）取决于该属性不同属性值的个数

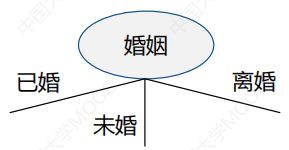
二元划分：划分数为2，这种划分要考虑创建k个属性值的二元划分的所有2^k-1-1种方法

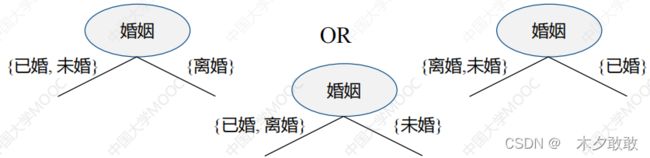
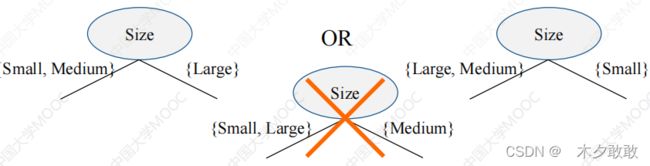
基于序数属性的划分

多路划分：划分数（输出数）取决于该属性不同属性值的个数

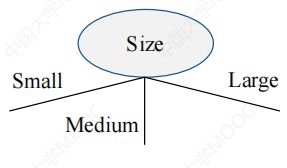
二元划分：划分数为2，这种划分要考虑创建k个属性值的二元划分的所有2^k-1-1种方法

基于连续属性的划分

多路划分：v_i≤ A < v_i+1 （i=1,…,k）
将连续变量分割成离散区间

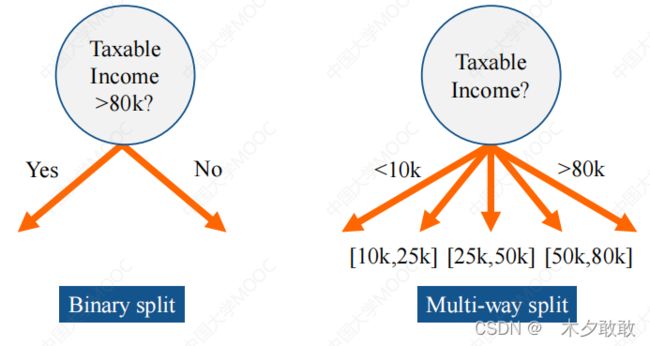
二元划分：（A < v）or （A ≥ v）
考虑所有的划分点，选择一个最优划分点v：从最小值开始建立分割区间，开始计算各自的信息增益，选择信息增益最大的一个分割区间作为最佳划分点

附：交叉验证（Cross Validation）

1. 基本思想

• 在某种意义下将原始数据(dataset)分组,一部分做为训练集(train set),另一部分做为验证集/测试集
(validation set or test set)
• 首先用训练集对分类器进行训练
• 再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。

2. 简单交叉验证

• 首先，随机的将样本数据分为两部分（比如70%的训练集，30%的测试集），然后用训练集来训练模型，在测试集上验证模型及参数
• 接着，再把样本打乱，重新选择训练集和测试集，继续训练数据和检验模型。
• 最后选择损失函数评估最优的模型和参数。

3. 留一法

• 当k=m 即k等于样本总数时，就是留一法。
• 每次的测试集都只有一个样本，要进行 m 次训练和预测。
• 这个方法用于训练的数据只比整体数据集少了一个样本，因此最接近原始样本的分布。
• 训练复杂度增加了
• 一般在数据缺乏时使用。

4. k-交叉验证

• 把样本数据随机的分成k份。
• 每一次挑选其中1份作为测试集，剩余 k-1 份作为训练集，训练后得到一个模型，计算并保存模型的评估指标。
• 重复 k 次，使得每个子集都有一次机会作为测试集。
• 计算 k 组测试结果的平均值作为模型的性能指标。
k 一般取10

代码

决策树