学习笔记2

感知机

基本概念

1.感知机接收多个输入信号，输出一个信号。感知机的信号也会形成流，向前方输送信息。但是，和实际的电 流不同的是，感知机的信号只有“流/不流”（1/0）两种取值。这里介绍的，0 对应“不传递信号”，1对应“传递信号”。
2.神经元会计算传送过来的信号的总和，只有当这个总和超过 了某个界限值时，才会输出1。这也称为“神经元被激活”。这里将这个界限值称为阈值，用符号θ表示。
3.感知机公式表达：

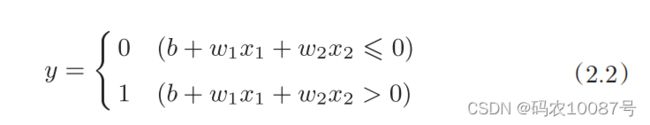
4.感知机的多个输入信号都有各自固有的权重，这些权重发挥着控制各个
信号的重要性的作用。也就是说，权重越大，对应该权重的信号的重要性就
越高。

感知机的简单实现

与门

# coding: utf-8
import numpy as np


def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])  # 0.5 0.5分别为 x1,x2的权重
    b = -0.7  # 0.7表示为阈值，线性变化后 b=-0.7
    tmp = np.sum(w * x) + b
    if tmp <= 0:
        return 0
    else:
        return 1


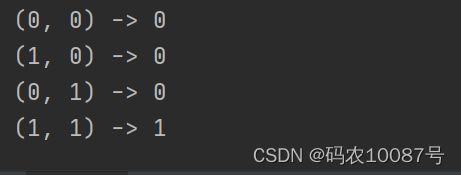
if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:  # 遍历每个元组
        y = AND(xs[0], xs[1])  # 元组中的索引为0 和 1的元素
        print(str(xs) + " -> " + str(y))

"""偏置和权重w1、w2的作用是不
一样的。具体地说，w1和w2是控制输入信号的重要性的参数，而偏置是调
整神经元被激活的容易程度（输出信号为1的程度）的参数。"""

输出结果：

非门

# coding: utf-8
import numpy as np


def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])    # 权重是自己想的
    b = 0.7                     # 阈值是0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

或门

# coding: utf-8
import numpy as np


def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w * x) + b
    if tmp <= 0:
        return 0
    else:
        return 1


if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

感知机（单层感知机）的局限性就在于它只能表示由一条直线分割的空间（ 感知机函数表达式就是线性的）。
感知机不能表示异或门，后续的学习可知多层叠加可以实现异或门。

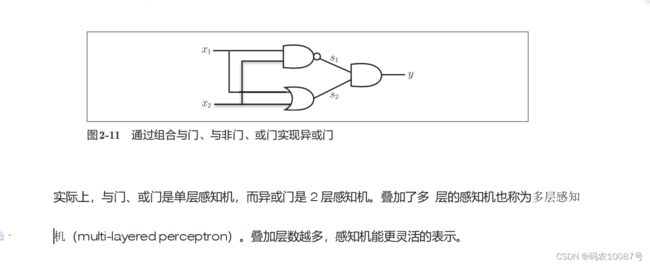
多层感知机叠加实现异或门

# coding: utf-8
from and_gate import AND
from or_gate import OR
from nand_gate import NAND


def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

小结：

机器学习的课题就是将决定参数值的工作交由计算机自动进行。学习是确定
合适的参数的过程，而人要做的是思考感知机的构造（模型），并把训练数据交给计算机。