入门机器学习（西瓜书+南瓜书）贝叶斯分类器总结（python代码实现）

入门机器学习（西瓜书+南瓜书）贝叶斯分类器总结（python代码实现）

一、贝叶斯分类器

1.1 通俗理解

先来看两个公式
$$P(AB)=P(A)P(B)（1）$$
$$P(AB)=P(B|A)P(A)=P(A|B)P(B)（2）$$
我先说第一个公式，首先这里的A，B分别代表两个不同的事件。如果事件A和事件B的独立，也就是说事件A的发生不影响事件B。事件B的发生不影响事件A。则$P(AB)=P(A)P(B)$。
如果，事件A是去KTV唱歌，事件B是买蜜雪冰城。那么A，B两个事件是互不影响的，即他们是独立的。
然后如果A，B两个事件相互影响，比如事件A是游客到景区购买索道门票。事件B是游客在景区座索道观光拍照。那么，显然事件B很依赖事件A。毕竟如果没有事件A，事件B不可能发生。因此，在这个情景，我们会把$P(B)$改为$P(B|A)$,即在事件A发生的前提下，事件B发生的概率。
理清楚了这个关系，亲爱的读者，你才有基本的数学基础来学习贝叶斯分类器，否则，大概率是学习的过程是一头雾水。
下面有请我们概率界的大哥——贝叶斯公式登场。或许有同学会问，为啥叫贝叶斯公式呢，因为这个公式是1763年由英国数学家托马斯贝叶斯的一篇论文中为解决一个逆概率问题提出的。因此被称为贝叶斯公式（定理）。
我们顶着公式（2）的后两项$P(B|A)P(A)=P(A|B)P(B)$，我做这样一个处理，等式两边分别除以$P(B)$，得到公式（3）
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}(3)$$
这就是贝叶斯公式，看似简单，但是为概率打开了一扇大门，如果说刚才我们的分析是从前到后，由因朔果，那么贝叶斯公式就是从后往前，由果朔因。通过这个公式得到的$P(B|A)$为事件A发生条件下，事件B发生的概率。
但是我们往往认为事件B会依赖事件A，而事件A不依赖于事件B。但是事实不是这样。实际上，贝叶斯公式反应的结果是，结果发生，条件发生的概率。
两者的关系是互项影响的。只是这个数值反映了两者影响的程度而已。
举个例子
你约你喜欢的女神看电影，他同意了，那么究竟她是否对你心动呢？
我们设：
P(s)是你女神暗恋你/无所谓的可能性分布
P(o)是观测值比如她同意跟你一起看电影
P(o|s)是在不同背景态度下她同意的可能性，可以看作她心中两个情绪小人对跟你一起看电影的不同态度
P(s|o)则是从可以看电影这个现实得到的各个态度的可能性
$$P(s|o)=\frac{P(o|s)}{P(o)}P(s)(3)$$

比如，现在你女神40%喜欢你，60%概率无所谓。如果女神喜欢你，那么你约她看电影的成功率是100%，如果无所谓，那么成功率只有30%。那么你约到女神出去的期望概率应该是40%*100%+60%*30%=58%。这也就是我们后面要讲的全概率公式。
最近一次，你又约了她，她答应了，那么那么女神到底喜不喜欢你呢？代入，在已知女神答应你去看电影的条件下，她喜欢你的概率是$\frac{0.4\ast 1}{0.58}=0.69$，无所谓的概率是$\frac{0.6\ast 3}{0.58}=0.31$，这也就说明了我们从女神答应你看电影这个结果，去推测女神是否喜欢我这个原因的概率。

1.2 全概率公式

在概率中，还有一个公式相当重要，他被叫做全概率公式。
我们现在再假设一个场景。小王要从家去公司上班，但是时间来不及了，路远的道路很耗费时间，路近的道路更容易堵车。我们可以跟据经验估计小王
选择每条路的概率，已经根据每条路的交通概况推测每条路通畅的概率。
选择每条路的概率分别为：0.5，0.3，0.2.每条路通畅的概率分别为：0.2，0.4，0.7

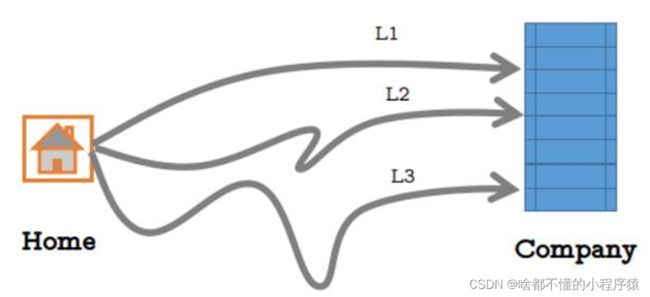
计算小明不迟到（不拥堵就不会迟到）的概率。
解：A，B1，B2，B3分别表示小明没有迟到，小明选择道路L1，道路L2，道路L3，则
$$\begin{array}{rl}P(A)& =P(A{B}_1)+P(A{B}_2)+P(A{B}_3)\\ & =P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+P(A|B_3)P(B_3)\\ & =0.2\times 0.5+0.4\times 0.3+0.7\times 0.2\\ & =0.36\end{array}$$
因此全概率公式，被定义为表示要达到某个目的，有多种方式（或者造成某种结果，有多种原因），问达到目的的概率是多少（或造成这种结果的概率是多少），若要达到目标$A$，有$n$种方式，记作$B1,B2,\dots ,Bn$ ，之间相互独立，并且其概率和为1。那么对于任意一个事件$A$发生的概率可以用下面的全概率公式计算：
$$\begin{array}{rl}P(A)& =P(A{B}_1)+P(A{B}_2)+...+P(A{B}_n)\\ & =P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+...+P(A|B_n)P(B_n)\\ & =\sum _{i=1}^{n}P(A|B_i)P(B_i)\end{array}$$

1.3 朴素贝叶斯分类器

给定 N 个类别，设随机样本向量$x=x_1,x_2,\dots ,x_d$ ，相关的三个概率：
（1）先验概率$P(c)$ ：根据以前的知识和经验得出的c类样本出现的概率，与现在无关。
（2）后验概率$P(c|x)$ ：相对于先验概率而言，表示x 属于c类的概率。
（3）条件概率$P(x|c)$ ：已知属于c类的样本中发生x的概率。

在朴素贝叶斯分类器：假设所有的属性都相互独立。
$$\begin{array}{rl}P(c|x)& =\frac{P(x|c)P(c)}{P(x)}\\ P(c|x)& =\frac{P(x_1,x_2,\dots ,x_d|c)P(c)}{P(x)}=\frac{P(c)}{P(x)}\prod _{i=1}^{d}P(x_i|c)\end{array}$$
$ma{x}_{c}P(c|x)=ma{x}_{c}P(c){\prod }_{i=1}^{d}P(x_i|c)$
先验概率：
$P(c)=\frac{|D_c|}{|D|}$,$D_c$表示训练集中类别为c的样本组成的集合
条件概率
离散属性：
$$P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}$$其中$D_{c,x{i}_i}$为第i个属性值为$x_i$样本组成的集合。
连续属性：
$$P(x_i|c)=\frac{1}{\sqrt{2\pi }{\sigma }_{c,i}}{e}^{-\frac{x_i-{\mu }_{c,i}}{2{\sigma }_{c,i}^2}}$$

1.4 拉普拉斯平滑

拉普拉斯平滑：为了避免其他属性携带的信息被其他未出现过的属性值“抹去”，在估计概率值时通常要进行平滑。即为了在$|D_c|$为0的基础上，对其分子加1，为了使得其不大于1，分母同时加上类别数（$N>=1$).因此概率被修正为一个很小但不为零的数。具体的说，令$N$表示训练集$D$中的类别数，$N_i$表示第$i$个属性可能的取值数，则：
$$P(c)=\frac{|D_c|+1}{|D|+N}$$
$$P(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}$$

二、代码实现

在这里我们介绍一下，sklearn的贝叶斯分类器，更多内容请关注sklearn官方链接，这里附上sklearn的中文社区，里面对每个函数都有详细的讲解和例子，sklearn中文社区

from sklearn.naive_bayes import GaussianNB, MultinomialNB,BernoulliNB

#GaussianNB：高斯分布的朴素贝叶斯
#MultinomialNB：多项式分布的朴素贝叶斯
#BernoulliNB：伯努利分布的朴素贝叶斯

#这里附上一个高斯分布的朴素分布的贝叶斯分类器简单使用，对鸢尾花数据集分类。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
print("Number of mislabeled points out of a total %d points : %d" % (X_test.shape[0], (y_test != y_pred).sum()))
#Number of mislabeled points out of a total 75 points : 4

这是一个利用朴素贝叶斯判断善意和恶意评论的一个例子。这是一个朴素贝叶斯应用的经典的例子

import numpy as np
from functools import reduce
'''
函数说明：创建实验样本
Parameters:
    无
Returns:
        postingList: 实验样本切分的词条
        classVec: 类别标签向量
'''
def loadDataSet():
    postingList = [['my','dog','has','files','problems','help','please'],#切分的词条
                   ['maybe','not','take','him','to','dog','park','stupid'],
                   ['my','dalmation','is','so','cute','I','love','him'],
                   ['stop','posting','stupid','worthless','garbage'],
                   ['mr','licks','ate','my','steak','how','to','stop'],
                   ['quit','buying','worthless','dog','food','stupid']]
    classVec = [0,1,0,1,0,1] #类别标签向量，1代表侮辱性词汇，0代表非侮辱性词汇
    return postingList,classVec #返回实验样本切分的向量词条和类别标签向量
'''
函数说明：将切分的实验样本词条整理成不重复的词条列表，也就是词汇表
Parameters:
    dataSet:整理的样本数据集
Returns:
    vocabSet:返回不重复的词条列表，也就是词汇表
'''
def createVocabList(dataSet):
    vocabSet = set([])                      #创建一个空的不重复列表
    for document in dataSet:
        vocabSet = vocabSet | set(document) #取并集
    return list(vocabSet)
'''
函数说明：根据vocabList词汇表，将inputSet向量化，向量的每个元素为1或0
Parameters:
    vocabList:createVocabList返回的列表
    inputSet:切分的词条列表
Returns:
    returnVec:文档向量，词集模型
'''
def setOfWords2Vec(vocabList,inputSet):             #创建一个其中所含元素都为0的向量
    returnVec = [0]* len(vocabList)                 #遍历每个词条
    for word in inputSet:                           #如果词条存在于词汇表中，则置1
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else:
            print("the word:%s is not in my Vocabulary!"%word)
    return returnVec                                #返回文档向量
'''
函数说明：朴素贝叶斯分类器训练函数
Parameters:
    trainMatrix:训练文档矩阵
    trainCategory:训练类别标签向量
Returns:
    p0Vect:侮辱类的条件概率数组
    p1Vect:非侮辱类的条件概率数组
    PAbusive:文档属于侮辱类的概率
'''
def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)         #计算训练的文档数目
    numWords = len(trainMatrix[0])          #计算每篇文档的词条数
    pAbusive = sum(trainCategory)/float(numTrainDocs)       #文档属于侮辱类的概率
    p0Num = np.zeros(numWords)
    p1Num = np.zeros(numWords)
    #创建numpt.zeros数组
    p0Denom = 0.0
    p1Denom = 0.0
    p1Vect = 0.0
    p0Vect = 0.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:           #统计属于侮辱类的条件概率所需的数据，即p(w0|1),p(w1|1),p(w2|2)...
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:                               #统计属于侮辱类的条件概率数组，属于非侮辱类的条件概率数组、文档属于侮辱类的概率
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    if(p1Denom!=0):
        p1Vect = p1Num/p1Denom              #相除
    if(p0Denom!=0):
        p0Vect = p0Num/p0Denom
    return p0Vect,p1Vect,pAbusive
        #返回属于侮辱类的条件概率数组、属于非侮辱类的条件概率数组，文档属于侮辱类的概率
'''
函数说明：朴素贝叶斯分类器分类函数
Parameters:
    vec2Classify:待分类的词条数组
    p0Vec:侮辱类的条件概率数组
    p1Vec:非侮辱类的条件概率数组
    pClass1:文档属于侮辱类的概率
Returns:
    0:属于非侮辱类
    1:属于侮辱类
'''
def classifyNB(vec2classify,p0Vec,p1Vec,pClass1):
    p1 = reduce(lambda x,y:x+y,vec2classify*p1Vec) * pClass1 #对应元素相乘
    p0 = reduce(lambda x,y:x+y,vec2classify*p0Vec) * (1.0 - pClass1)
    print('p0:',p0)
    print('p1:',p1)
    if(p1>p0):
        return 1
    else:
        return 0
'''
函数说明：测试朴素贝叶斯分类器
Parameters:
    无
Returns:
    无
'''
def testingNB():
    listOPosts,listClasses = loadDataSet()              #创建实验样本
    myvocabList = createVocabList(listOPosts)           #创建词汇表
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myvocabList,postinDoc))           #将实验样本向量
        p0v,p1v,pAb = trainNB0(np.array(trainMat),np.array(listClasses)) #朴素贝叶斯分类器

    testEntry = ['love', 'my','dalmation']                               #测试样本1
    #测试样本向量化
    thisDoc = np.array(setOfWords2Vec(myvocabList, testEntry))
    if classifyNB(thisDoc, p0v, p1v, pAb):
        print(testEntry, '属于侮辱类')                                     #执行分类并打印分类结果
    else:
        print(testEntry, '属于非侮辱类')                                   #执行分类并打印分类结果

    testEntry = ['stupid','garbage']
    #测试样本向量化
    thisDoc = np.array(setOfWords2Vec(myvocabList,testEntry))            #测试样本2
    if classifyNB(thisDoc,p0v,p1v,pAb):
        print(testEntry,'属于侮辱类')                                      #执行分类并打印分类结果
    else:
        print(testEntry,'属于非侮辱类')                                     #执行分类并打印分类结果
if(__name__=='__main__'):
    testingNB()

结果如图

p0: 0.10869565217391304
p1: 0.0
['love', 'my', 'dalmation'] 属于非侮辱类
p0: 0.0
p1: 0.10526315789473684
['stupid', 'garbage'] 属于侮辱类

结果分析，可以看到部分概率为0，这样的结果过于绝对，容错率偏低，我们可以尝试加入拉普拉斯平滑，来对概率进行修正。

三、代码文件

小程序员将代码文件和相关素材整理到了百度网盘里，因为文件大小基本不大，大家也不用担心限速问题。后期小程序员有能力的话，将在gitee或者github上上传相关素材。
链接：https://pan.baidu.com/s/1Ce14ZQYEYWJxhpNEP1ERhg?pwd=7mvf
提取码：7mvf