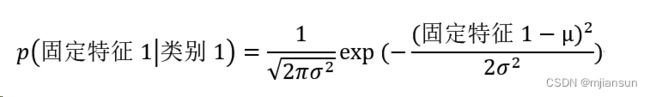【概率图模型】（一）高斯朴素贝叶斯分类器(原理+python实现）

1.原理

具体例子

我们通过判定花萼长度，花萼宽度，花瓣长度，花瓣宽度的尺寸大小来识别鸢尾花的类别。关于数据集，是通过sklean加载而来，这次只采用前一百个数据进行训练，使得花的类别只有0和1两个类别，因此我们这次目标是通过花的四个特征来判断类别是0还是1。

from sklearn.datasets import load_iris
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, :])
    print(data)
    return data[:,:-1], data[:,-1]

根据贝叶斯准则，可以得到在固定特征下，每个类别的概率，其表达式具体如下：

如果p(类别1│固定特征) > p(类别2│固定特征)，则在给出的特征下，类别属于1的概率大，因此预测类别为1，可以看出贝叶斯决策理论是通过计算概率，选择概率较大的来预测类别。
需要注意的是，p(固定特征│类别i)中的固定特征有4个，如果假设各个特征是相互独立的，则可以写成(之所以在贝叶斯前面加上朴素，正是这个独立性假设)：

• p(固定特征1│类别i)*p(固定特征2│类别i)*p(固定特征3│类别i)p(固定特征4│类别i)

那么针对p(固定特征1│类别1)而言，当选择高斯模型时，可以通过下述公式计算：

其中，σ^2和μ表示为方差和期望，是通过在类别1的训练样本里，计算出特征1的方差和期望，固定特征1表示为特征1的一个固定值，因此可以根据测试数据中一个数据的特征1的值来计算出该数据的p(固定特征1│类别1)。
看到这里，可能会想，为什么p(固定特征1│类别1)时， 为何要用高斯概率分布函数来计算概率呢？
这是因为数据集的特征都是属于连续型的特征，并非离散型，所以当给出一个具体的特征值的时候，是无法通过数据集来计算出该特征值的概率，此外，数据集的样本数一般也较少，无法将特征值划分到某个区间来计算概率。因此，当遇到这样的问题时，我们假设特征的分布是符合高斯分布，那么就可以通过该分布函数计算出任意特征值所对应的概率，所以p(固定特征1│类别1)的问题也就解决了。

2.代码实现逻辑

输入训练集数据
输入测试集数据
对于每一个类别i：
    对于每一个特征j：
        计算训练集的方差，期望
        根据测试集来计算p(固定特征j│类别i)
根据测试集来计算p_i=p(固定特征│类别i)* p(类别)
根据p_i相对大小，返回预测类别
计算分类正确率

3.代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import math
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, :])
    print(data)
    return data[:,:-1], data[:,-1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
class NaiveBayes:
    def __init__(self):
        self.model = None
    # 数学期望
    @staticmethod  # 在def方法中没有引用对象的资源时，要加上这个
    def mean(X):  # 这表明mean这个函数里面不需要调用self.的对象和调用
        return sum(X) / float(len(X))
    # 标准差（方差） X是所有样本同一特征下的各个值
    def stdev(self, X):  # 这里就不能加@staticmethod，因为他要用刚才定义好的函数mean
        avg = self.mean(X)  # 依然是用self来引用函数
        return math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))
    # 概率密度函数  x结构为一个数据，其格式为[第一个特征, 第二个特征]
    def gaussian_probability(self, x, mean, stdev):
        exponent = math.exp(-(math.pow(x - mean, 2) / (2 * math.pow(stdev, 2))))
        return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent

    # 处理X_train
    def summarize(self, train_data):  # train_data结构为[array[5.0, 0.37],array[3.42, 0.40],array[3.42, 0.40],[12, 0.40]..]
        summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]  # zip(*)作用将train_data转置，
        # 变为 [array[5.0, 3.42, 12], array[0.37, 0.4, 0.4]]
        return summaries

    # 分类别求出数学期望和标准差    self.model的数据结构{类别1：第一个特征期望和方差，第二个特征的期望和方差
    #                                                    类别2：第一个特征期望和方差，第二个特征的期望和方差}
    def fit(self, X, y):
        labels = list(set(y))  # 集合是{} 列表是[] 所以要list回来
        data = {label: [] for label in labels}  # 创建个字典，每个键的值是列表
        for f, label in zip(X, y):  # zip将对象相应位置元素打包成元组，然后返回元组组成的列表，结构为(array([X]), y),...
            data[label].append(f)  # 构建data{y1:[array(x1),array(x2),..],y2:[array(x1),array(x2),..]..}
        self.model = {
            label: self.summarize(value)  # value为键的值，即[array(x1),array(x2),..]
            for label, value in data.items()
        }
        return 'gaussianNB train done!'

    # 计算概率 probabilities的结构为{0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
    def calculate_probabilities(self, input_data):
        # input_data[i]:[1.1, 2.2]
        probabilities = {}
        for label, value in self.model.items():
            probabilities[label] = 1
            for i in range(len(value)):
                mean, stdev = value[i]
                probabilities[label] *= self.gaussian_probability(
                    input_data[i], mean, stdev)
        return probabilities

    # 选出概率大所对应的类别
    def predict(self, X_test):
        # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
        label = sorted(
            self.calculate_probabilities(X_test).items(),  # 字典就要加items()来列出所有的键和值，结构为[(0.0: 2.968), (1.0: 3.89)]
            key=lambda x: x[-1])[-1][0]
        return label

    def score(self, X_test, y_test):
        right = 0
        for X, y in zip(X_test, y_test):
            label = self.predict(X)
            if label == y:
                right += 1

        return right / float(len(X_test))

运行分类器，测试花萼长度，花萼宽度，花瓣长度，花瓣宽度为 [4.4, 3.2, 1.3, 0.2]时，可以预测花的类别即正确率

# 运行分类器
model = NaiveBayes()
model.fit(X_train, y_train)
print(model.predict([4.4,  3.2,  1.3,  0.2]))
model.score(X_test, y_test)

类别为0，预测正确

4.补充例子

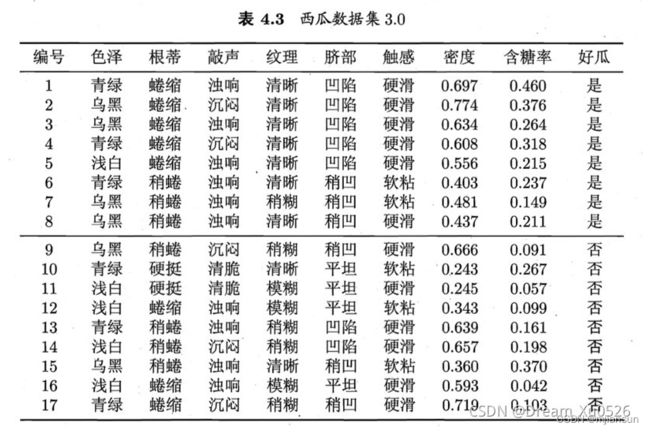
下面用一个实例来说明一下：
我们首先先给出训练集和测试数据；

首先先计算先验概率；

然后再计算条件概率；
这个地方需要注意一下，密度和甜度这种程度的属性需要使用概率密度函数来进行计算。

 将好瓜与坏瓜的先验概率和条件概率分别进行累乘。

然后我们对累乘的结果进行比较，可以很明显看出来是好瓜的概率大于是坏瓜的概率，因此我们测试的瓜系统给出为好瓜。

5.优缺点

• 优点

1. 对待预测样本进行预测，过程简单速度快(想想邮件分类的问题，预测就是分词后进行概率乘积，在log域直接做加法更快)。
2. 对于多分类问题也同样很有效，复杂度也不会有大程度上升。
3. 在分布独立这个假设成立的情况下，贝叶斯分类器效果奇好，会略胜于逻辑回归，同时我们需要的样本量也更少一点。
4. 对于类别类的输入特征变量，效果非常好。对于数值型变量特征，我们是默认它符合正态分布的。

• 缺点

1. 对于测试集中的一个类别变量特征，如果在训练集里没见过，直接算的话概率就是0了，预测功能就失效了。当然，我们前面的文章提过我们有一种技术叫做『平滑』操作，可以缓解这个问题，最常见的平滑技术是拉普拉斯估测。
2. 那个…咳咳，朴素贝叶斯算出的概率结果，比较大小还凑合，实际物理含义…恩，别太当真。
3. 朴素贝叶斯有分布独立的假设前提，而现实生活中这些predictor很难是完全独立的。

6.最常见应用场景

• 文本分类/垃圾文本过滤/情感判别：这大概会朴素贝叶斯应用做多的地方了，即使在现在这种分类器层出不穷的年代，在文本分类场景中，朴素贝叶斯依旧坚挺地占据着一席之地。原因嘛，大家知道的，因为多分类很简单，同时在文本数据中，分布独立这个假设基本是成立的。而垃圾文本过滤(比如垃圾邮件识别)和情感分析(微博上的褒贬情绪)用朴素贝叶斯也通常能取得很好的效果。
• 多分类实时预测：这个是不是不能叫做场景？对于文本相关的多分类实时预测，它因为上面提到的优点，被广泛应用，简单又高效。
• 推荐系统：是的，你没听错，是用在推荐系统里！！朴素贝叶斯和协同过滤(Collaborative Filtering)是一对好搭档，协同过滤是强相关性，但是泛化能力略弱，朴素贝叶斯和协同过滤一起，能增强推荐的覆盖度和效果。

参考

朴素贝叶斯分类器_Dream_Xu0526的博客-CSDN博客_朴素贝叶斯分类器

机器学习：高斯朴素贝叶斯分类器(原理+python实现）_DocPark的博客-CSDN博客_高斯朴素贝叶斯分类器