数字图像处理 图像锐化
目录
- 微分法
微分法
有Laplace算符: ∇ = [ ∂ ∂ x ∂ ∂ y ] \nabla= \left [ \begin{matrix} \frac{\partial }{\partial x} \\\frac{\partial }{\partial y} \end{matrix} \right ] ∇=[∂x∂∂y∂]
对于数字图像,梯度是由差分来表示的: { G x = f ( x + 1 , y ) − f ( x , y ) G y = f ( x , y + 1 ) − f ( x , y ) \left\{\begin{matrix}G_x=f\left( x+1,y\right)-f\left( x,y \right) \\G_y=f\left( x,y+1\right)-f\left( x,y \right) \end{matrix}\right. {Gx=f(x+1,y)−f(x,y)Gy=f(x,y+1)−f(x,y)即: ∇ f = [ Δ x f Δ y f ] T \nabla f=\left [ \begin{matrix}\Delta _xf&\Delta _yf \end{matrix} \right ]^T ∇f=[ΔxfΔyf]T
还有罗伯特算法: { G x = f ( x + 1 , y + 1 ) − f ( x , y ) G y = f ( x , y + 1 ) − f ( x + 1 , y ) \left\{\begin{matrix}G_x=f\left( x+1,y+1\right)-f\left( x,y \right) \\G_y=f\left( x,y+1\right)-f\left( x+1,y \right) \end{matrix}\right. {Gx=f(x+1,y+1)−f(x,y)Gy=f(x,y+1)−f(x+1,y)
常采用绝对差算法来提高运算速度: ∣ G ( x , y ) ∣ = ∣ f ( x + 1 , y + 1 ) − f ( x , y ) ∣ + ∣ f ( x , y + 1 ) − f ( x + 1 , y ) ∣ \left | G(x,y) \right |=\left | f\left( x+1,y+1\right)-f\left( x,y \right) \right |+\left |f\left( x,y+1\right)-f\left( x+1,y \right) \right | ∣G(x,y)∣=∣f(x+1,y+1)−f(x,y)∣+∣f(x,y+1)−f(x+1,y)∣
代码实现:
def roberts(img):
m = img.shape[0]
n = img.shape[1]
img1 = np.zeros((m, n, 3), np.uint8)
for i in range(m-1):
for j in range(n-1):
for k in range(3):
img1[i, j, k] = np.sqrt((-img[i, j, k]+img[i+1, j+1, k])**2 +
(img[i+1, j, k]-img[i, j+1, k])**2)
#这里稍作修改就是绝对值差和
return img1

|

|
|---|---|

|

|
上面四张图片分别是用水平垂直差分法和罗伯特算法实现的。
 |
 |
 |
|---|
def roberts(img):
m = img.shape[0]
n = img.shape[1]
img1 = np.zeros((m, n, 3), np.uint8)
for i in range(m-1):
for j in range(n-1):
img1[i, j] = img[i, j]+np.uint8(0.1*np.sqrt((-img[i, j]+img[i+1, j+1])**2 +
(img[i+1, j]-img[i, j+1])**2))
return img1
除此之外,还有一些常用的算符。
使用内置库更为方便:
from skimage import filters
import cv2
import numpy as np
import matplotlib.pyplot
img = cv2.imread('hzyRoberts000.jpg', 0)
img_robert_pos = filters.roberts_pos_diag(img)
img_robert_neg = filters.roberts_neg_diag(img)
img_robert_nom = filters.roberts(img)
cv2.imshow('nom', img_robert_nom)
cv2.imshow('neg', img_robert_neg)
cv2.imshow('pos', img_robert_pos)
cv2.imwrite('hzyRoberts003.jpg', img_robert_pos*255)
cv2.imwrite('hzyRoberts004.jpg', img_robert_neg*255)
cv2.imwrite('hzyRoberts005.jpg', img_robert_nom*255)
cv2.waitKey(0)
cv2.destroyAllWindows()
效果如图:
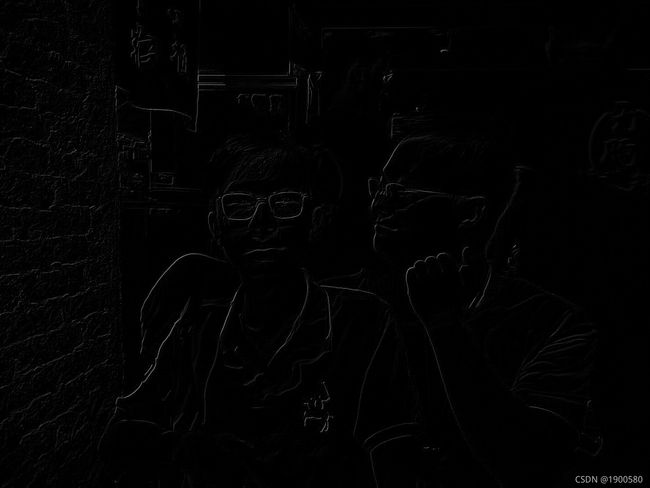 |
 |
 |
|---|
