FCN(Fully Convolutional Networks for Semantic Segmentation)---2015 CVPR学习和解读
最近关于 A n c h o r F r e e Anchor \ Free Anchor Free的目标检测结构如雨后春笋般出现,我也跟一波学习,发现,里面涉及到很多细碎的知识,没办法啊,只有一层一层拨开它的心!道阻且长啊~~~~~写的不好望指点哈!旨在学习交流,最重要的还是记录!
F C N ( F u l l y C o n v o l u t i o n a l N e t w o r k s f o r S e m a n t i c S e g m e n t a t i o n ) − − − 2015 C V P R FCN \ (Fully \ Convolutional \ Networks \ for \ Semantic \ Segmentation)---2015 \ CVPR FCN (Fully Convolutional Networks for Semantic Segmentation)−−−2015 CVPR
文章目录
- 1、引言
- 2、网络结构
-
- 2.1 全卷积网络提取特征
- 2.2 逐像素点分类
- 2.3 损失函数
- 3、训练过程
- 4、参考链接
1、引言
图像语义分割:给定一张图片,对图片上每一个像素点进行分类!但是与图像分类目的不同,语义分割模型要具有像素级的密集预测能力才可以。

传统的 C N N CNN CNN做语义分割:将像素周围的一块(一个小区域)作为 C N N CNN CNN的输入,也就是利用每个像素周围的图像块所属类别将该像素分成该类别。简单的说:以某个像素点中心取一个区域,取图像块的特征做样本训练分类器,分类结果作为此像素点的结果。使用这种方法的主要原因是网络后面具有全连接层,全连接层输入需要固定大小。
上述存在三个缺点:
- 这个像素周围一块的大小如何确定;
- 明显存储量和计算量很大(因为图像块会有很多重复的地方);
- 像素周围一块是局部,会限制感受野,难以照顾全局;
然后就出现了这篇文章: F C N ( F u l l y C o n v o l u t i o n a l N e t w o r k s f o r S e m a n t i c S e g m e n t a t i o n ) − 2015 C V P R FCN \ (Fully \ Convolutional \ Networks \ for \ Semantic \ Segmentation)-2015 \ CVPR FCN (Fully Convolutional Networks for Semantic Segmentation)−2015 CVPR。改变了原来的 C N N CNN CNN结构,去除了全连接层,进行密集预测。
除了全连接层结构,池化层也是语义分割里面一个棘手的问题。池化层可以丢弃部分位置信息,增大感受野。这对识别有帮助,因为不需要位置空间信息。但是语义分割方法需对类别图进行精确调整,因此需要保留位置信息。这篇论文中使用上采样来逐步恢复细节和相应的位置信息。
2、网络结构
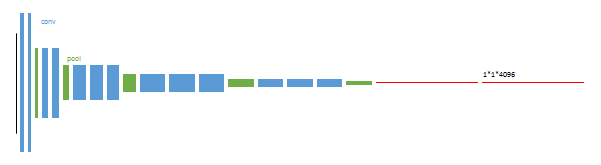
先简单介绍一下 F C N FCN FCN:全卷积网络,模型由卷积层、池化层组成(没有全连接层),可以接受任意大小的输入,网络的示意图如下:
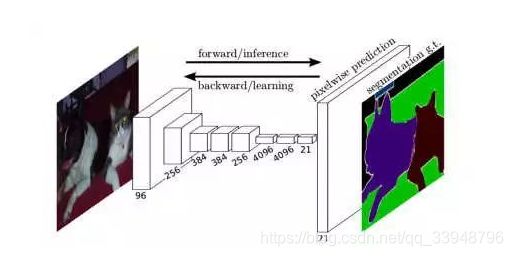 输入一张图片,网络由浅到深,随着卷积层和池化层不断作用,产生的特征图分辨率越来越小,但是通道数会越来越多。最后通过逐层上采样得到一个和输入形状一样的结果。
输入一张图片,网络由浅到深,随着卷积层和池化层不断作用,产生的特征图分辨率越来越小,但是通道数会越来越多。最后通过逐层上采样得到一个和输入形状一样的结果。
2.1 全卷积网络提取特征
一般图像分类 C N N CNN CNN网络在最后一层卷积层后会跟若干个全连接层, 作用:将卷积层产生的特征图映射成一个固定长度的特征向量。论文中的例子:输入一张猫的图片, 经过 C N N CNN CNN网络, 得到一个长为1000的输出向量, 这个向量经过 S o f t m a x Softmax Softmax归一化,分别对应1000个类别的概率,这样我们可以得到输入图像属于每一类的概率, 在下例中我们可以看出图像属于 “ t a b b y c a t ” “tabby \ cat” “tabby cat”这一类可能性最大。
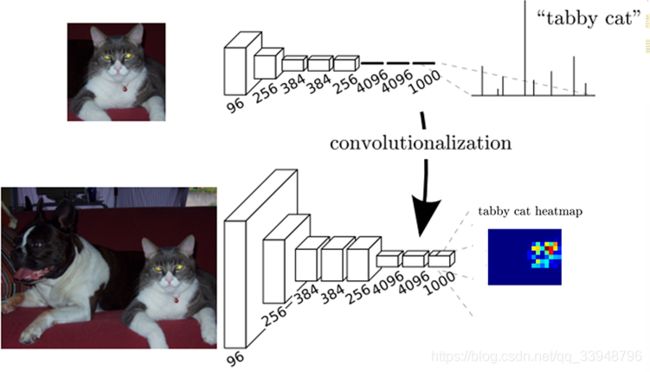 这篇论文里面是将全连接层转化为卷积层。上图中我们可以看出 F C N FCN FCN将最后3层转换为卷积层,卷积核的大小(通道数,宽,高)分别为(4096,1,1)、(4096,1,1)、(1000,1,1)。
这篇论文里面是将全连接层转化为卷积层。上图中我们可以看出 F C N FCN FCN将最后3层转换为卷积层,卷积核的大小(通道数,宽,高)分别为(4096,1,1)、(4096,1,1)、(1000,1,1)。
下面介绍全连接层怎么转成卷积层:拿上图为例,最后一层卷积层的输出为 7 ∗ 7 ∗ 256 7*7*256 7∗7∗256 。后面再接三个全连接层变为(1,4096),(1,4096),(1,1000)(一维向量)。我们可以把这三个全连接层变为卷积层。
变换方式:
- 针对 F C 1 ( 7 ∗ 7 ∗ 256 ) FC1(7*7*256) FC1(7∗7∗256),选卷积核 k = 7 k=7 k=7卷积,输出为 1 ∗ 1 ∗ 4096 1*1*4096 1∗1∗4096。
- 针对 F C 2 FC2 FC2,选卷积核 k = 1 k=1 k=1卷积,输出为 1 ∗ 1 ∗ 4096 1*1*4096 1∗1∗4096。
- 对最后一个 F C 3 FC3 FC3,选卷积核 k = 1 k=1 k=1卷积,输出为 1 ∗ 1 ∗ 1000 1*1*1000 1∗1∗1000。
这样转换后的网络输出的就是一个热力图 ( h e a t m a p ) (heatmap) (heatmap),这个图明显二维的。
2.2 逐像素点分类
参考自:(https://zhuanlan.zhihu.com/p/30195134)
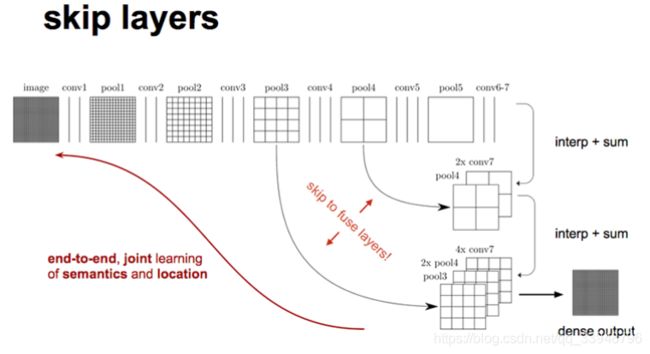 我们可以看出,对原图像进行卷积 c o n v 1 、 p o o l 1 conv1、pool1 conv1、pool1后原图像缩小为1/2;之后对图像进行第二次 c o n v 2 、 p o o l 2 conv2、pool2 conv2、pool2后图像缩小为1/4;接着继续对图像进行第三次卷积操作 c o n v 3 、 p o o l 3 conv3、pool3 conv3、pool3缩小为原图像的1/8,此时保留 p o o l 3 pool3 pool3的 f e a t u r e M a p feature \ Map feature Map;接着继续对图像进行第四次卷积操作 c o n v 4 、 p o o l 4 conv4、pool4 conv4、pool4,缩小为原图像的1/16,保留 p o o l 4 pool4 pool4的 f e a t u r e M a p feature \ Map feature Map;最后对图像进行第五次卷积操作 c o n v 5 、 p o o l 5 conv5、pool5 conv5、pool5,缩小为原图像的1/32,然后把原来CNN操作中的全连接变成卷积操作 c o n v 6 conv6 conv6,图像的 f e a t u r e M a p feature \ Map feature Map数量改变但是图像大小依然为原图的1/32,此时图像不再叫 f e a t u r e M a p feature \ Map feature Map而是叫 h e a t M a p heatMap heatMap(热力图)。
我们可以看出,对原图像进行卷积 c o n v 1 、 p o o l 1 conv1、pool1 conv1、pool1后原图像缩小为1/2;之后对图像进行第二次 c o n v 2 、 p o o l 2 conv2、pool2 conv2、pool2后图像缩小为1/4;接着继续对图像进行第三次卷积操作 c o n v 3 、 p o o l 3 conv3、pool3 conv3、pool3缩小为原图像的1/8,此时保留 p o o l 3 pool3 pool3的 f e a t u r e M a p feature \ Map feature Map;接着继续对图像进行第四次卷积操作 c o n v 4 、 p o o l 4 conv4、pool4 conv4、pool4,缩小为原图像的1/16,保留 p o o l 4 pool4 pool4的 f e a t u r e M a p feature \ Map feature Map;最后对图像进行第五次卷积操作 c o n v 5 、 p o o l 5 conv5、pool5 conv5、pool5,缩小为原图像的1/32,然后把原来CNN操作中的全连接变成卷积操作 c o n v 6 conv6 conv6,图像的 f e a t u r e M a p feature \ Map feature Map数量改变但是图像大小依然为原图的1/32,此时图像不再叫 f e a t u r e M a p feature \ Map feature Map而是叫 h e a t M a p heatMap heatMap(热力图)。
现在我们有1/32尺寸的 h e a t M a p heatMap heatMap,1/16尺寸的 f e a t u r e M a p feature \ Map feature Map和1/8尺寸的 f e a t u r e M a p feature \ Map feature Map,1/32尺寸的 h e a t M a p heatMap heatMap进行上采样操作之后,因为这样的操作还原的图片仅仅是conv5中的卷积核中的特征,限于精度问题不能够很好地还原图像当中的特征,因此把conv4中的卷积核对上一次上采样之后的图进行反卷积,最后把conv3中的卷积核对刚才上采样之后的图像进行再次反卷积补充细节,最后相加,完成了整个图像的还原。
其中上采样有3种常见的方法:双线性插值,反卷积(转置卷积),反池化。这边我只讨论反卷积。
反卷积(转置卷积):反卷积是一种特殊的正向卷积,先按照一定的比例通过补 0 来扩大输入图像的尺寸,接着卷积核卷积,再进行正向卷积。简单点说把普通卷积中的卷积核做一个转置,然后把普通卷积的输出作为转置卷积的输入,而转置卷积的输出,就是普通卷积的输入,常用于 C N N CNN CNN中对特征图进行上采样,比如语义分割和超分辨率任务中。我认为:反卷积就是卷积,只是中间 p a d d i n g padding padding下,然后再做卷积。
下面是常规的普通卷积:卷积核为 3 ∗ 3 3*3 3∗3, s t r i d e = 2 stride=2 stride=2, p a d d i n g = 1 padding=1 padding=1。卷积核在红框位置时输出元素1,在绿色位置时输出元素2。我们可以观察到:输入元素 a a a仅和一个输出元素有运算关系,也就是元素1,而输入元素 b b b和输出元素1, 2均有关系。同理 c c c只和一个元素2有关,而 d d d和1,2,3,4四个元素都有关。那么在进行反卷积时,依然应该保持这个连接关系不变。
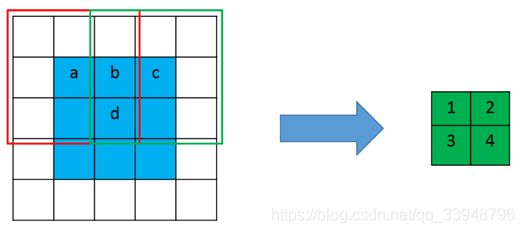
反卷积(转置卷积):由前面反卷积的定义,将上图得到的绿色特征图作为输入,蓝色特征图作为输出,并且需要保证连接关系不变。也就是说,a只和1有关,b和1,2两个元素有关,其它类推。怎么才能达到这个效果呢(一开始我个人觉得达不到。因为反卷积是可以恢复到原来输入的shape,但是其value值是不一样的?但是先进行上采样,即扩大像素;再进行卷积——就是通过训练学习获得权值,这就有可能了!)。
如下图:
设反卷积的输入是 n ∗ n n*n n∗n,反卷积的输出为 m ∗ m m*m m∗m, p a d d i n g = p padding=p padding=p, s t r i d e = s stride=s stride=s。
条件: ( n + 2 p − k ) % s = 0 (n+2p-k)\%s=0 (n+2p−k)%s=0,根据步数 s t r i d e s strides strides 对输入的内部进行填充,这里 s t r i d e s strides strides 可以理解成输入放大的倍数,即在 i n p u t input input 的每个元素之间填充 0 ,0 的个数 n 1 n_1 n1 与 s t r i d e s strides strides 的关系为: n 1 = s t r i d e s − 1 n_1=strides-1 n1=strides−1那么此时反卷积的输出就为: m = s ( n − 1 ) + k − 2 p m=s(n-1)+k-2p m=s(n−1)+k−2p
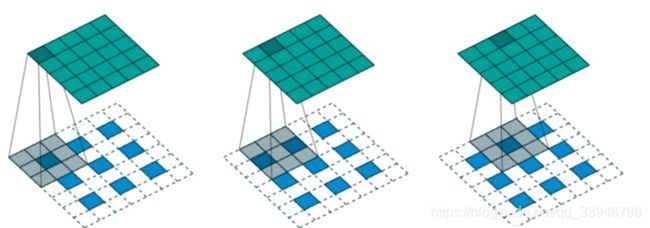
举个例子:选择一个输入 i n p u t input input尺寸为 3 × 3 3 \times 3 3×3 ,卷积核 k e r n e l kernel kernel 尺寸为 3 × 3 3\times 3 3×3 ,步长 s t r i d e s = 2 strides=2 strides=2 ,填充 p a d d i n g = 1 padding=1 padding=1,即 n = 3 , k = 3 , s = 2 , p = 1 n=3,k=3,s=2,p=1 n=3,k=3,s=2,p=1 ,则输出 o u t p u t output output 的尺寸为 m = 2 × ( 3 − 1 ) + 3 = 5 m=2\times(3-1)+3=5 m=2×(3−1)+3=5 。
2.3 损失函数
卷积网络中的每一层数据都是尺寸为 h ∗ w ∗ d h*w*d h∗w∗d的三维数组,其中 h h h和 w w w是特征图的高和宽, d d d是通道数。 F C N FCN FCN网络的训练损失为最后一层中每个像素的 S o f t m a Softma Softmax损失之和。更具体地说,最后上采样个跳层连接之后会输出 N N N张热力图 ( h e a t m a p ) (heatmap) (heatmap),逐个像素的求其在 N N N张图像该像素位置的最大数值描述(概率)作为该像素的分类。
3、训练过程
值得研究,体现思想!实验结果不贴!
- 最后两层是全连接层,参数弃去不用。
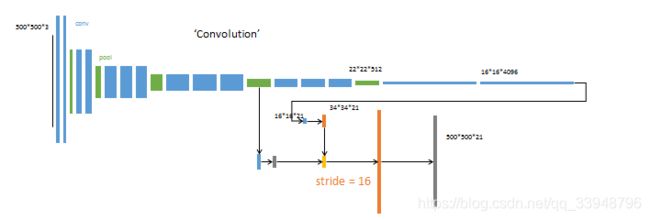
- 从最后一个特征图(16164096)预测分割小图(161621),然上采样为原图大小。反卷积(橙色)的步长为32所以网络称为FCN-32s。
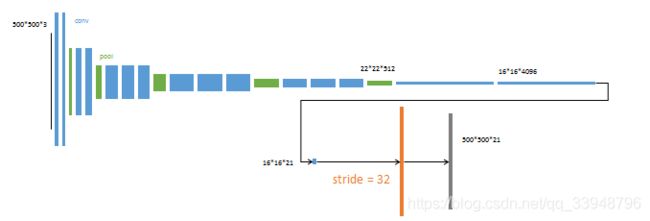
- 上采样融合2个pooling层的预测结果 。使用跳级结构提升精确性。第二次反卷积步长为16,这个网络称为FCN-16s。
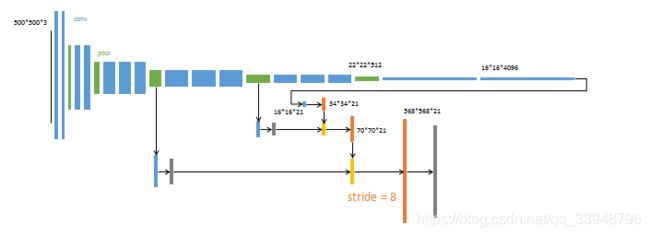
4. 上采样融合3个pooling层的预测结果。 第三次反卷积步长为8,记为FCN-8s。
4、参考链接
- https://zhuanlan.zhihu.com/p/30195134(重点推荐)
- https://blog.csdn.net/isMarvellous/article/details/80087705
- https://www.zhihu.com/search?type=content&q=转置卷积
- https://blog.csdn.net/attitude_yu/article/details/84697181(重点推荐)
- https://blog.csdn.net/qq_37274615/article/details/73251503(重点推荐)