【论文阅读】Fully Convolutional Networks for Semantic Segmentation【CVPR,PAMI】
摘要
- 我们的研究表明,卷积网络通过端到端、像素到像素的训练,在语义分割方面比之前的最佳结果有所提高
- 我们的关键见解是构建完全卷积网络,它接受任意大小的输入,并产生相应大小的输出,并具有有效的推理和学习
- 我们将当代分类网络(AlexNet、VGG net和GoogLeNet)适应为完全卷积网络,并通过微调将学到的表示转移到分割任务中
- 定义了一个跳跃架构,它结合了来自深层、粗层的语义信息和来自浅层、细层的外观信息,以产生精确和详细的分割
- 我们的全卷积网络实现了PASCAL VOC、NYUDv2、SIFT Flow和PASCAL- context的改进分割(相对于2012年67.2%的平均IU,提高了30%),而对典型图像的推理只需要十分之一秒
1 Introduction
- 之前的方法使用convnets进行语义分割,其中每个像素都被标记为其外围对象或区域的类别
- 学习和推理都是通过密集前馈计算和反向传播,每次全图像进行,如图1所示
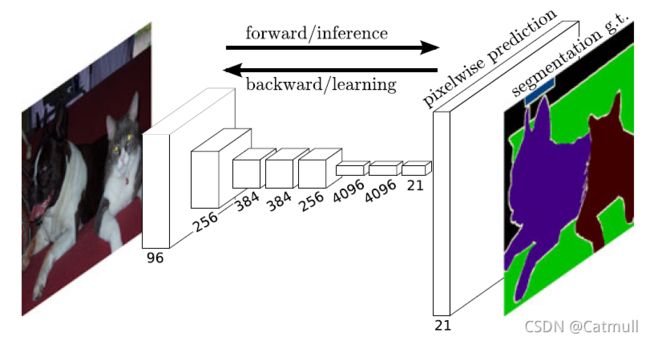
- 我们的方法不使用预处理和后处理的复杂性,包括超像素,proposals,或随机字段或局部分类器的事后细化
- 语义分割面临语义和位置之间的内在矛盾关系:全局信息解决what问题,而局部信息解决where问题。
- 调优优化可以带来更精确的网络,并且可以一次性学习跳过架构,而不是分阶段学习。
2 Related Work
-
Fully convolutional networks
-
Dense prediction with convnets
这些方法的共同要素包括:
(1)小模型限制容量和感受野
(2)patchwise training
(3)通过超像素投影、随机场正则化、滤波或局部分类进行细化
(4)"交错"以获得密集的输出
(5)多尺度金字塔处理
(6)饱和双曲正切非线性
(7)ensembles
与这些现有的方法不同,我们适应并扩展了深度分类架构,使用图像分类作为监督前训练,并对完全卷积进行微调,以简单有效地从整个图像输入和整个image ground thruths -
结合特征层次
我们跨层融合特性,以定义一个非线性的局部到全局表示,并对其进行端到端调优 -
FCN扩展
在本文的会议版本之后,fcn被扩展到新的任务和数据。任务包括区域建议、轮廓检测、深度回归、光流和弱监督语义分割。此外,新的工作改进了本文提出的fcnn,进一步推进了语义分割的技术水平。DeepLab模型通过空洞卷积和密集CRF推理提高输出分辨率。联合CRFasRNN模型是对CRF进行端到端的整合,以进一步改进。ParseNet规范融合功能,并使用全局池捕获上下文。反卷积网络方法通过建议、学习到的反卷积和上池化来恢复分辨率。
3 FULLY CONVOLUTIONAL NETWORKS
- 卷积网络的每一层输出都是大小为 h × w × d h \times w \times d h×w×d的三位数组, h h h和 w w w是空间维度, d d d是特征或者通道维度。第一层是图片, h × w h \times w h×w个像素, d d d个通道。较高层的位置对应于它们路径连接到的图像中的位置,这被称为它们的感受野
- 令 x ⃗ i j \vec x_{ij} xij代表某一层在位置 ( i , j ) (i,j) (i,j)处的数据向量, y ⃗ i j \vec y_{ij} yij代表下一层的,则 y ⃗ i j = f k s ( { x ⃗ s i + δ i , s j + δ j } 0 ≤ δ i , δ j ≤ k ) (1) \vec y_{ij}=f_{ks}( \{\vec x_{si+\delta i,sj+\delta j} \}_{0\leq \delta i,\delta j\leq k}) \tag 1 yij=fks({xsi+δi,sj+δj}0≤δi,δj≤k)(1), k k k是卷积核大小, s s s是步幅或下采样系数, f k s f_{ks} fks决定了这一层的类型:可能是卷积做的矩阵乘法,或者平均池化,或者最大池化,或者一个激活函数的元素间的非线性操作,等等。
- 这种函数的形式在分解下保存,卷积核大小和步幅遵循以下的变换规则:
f k s ○ g k ′ s ′ = ( f ○ g ) k ′ + ( k − 1 ) s ′ , s s ′ (2) f_{ks}○ g_{k's'}=(f○g)_{k'+(k-1)s',ss'} \tag 2 fks○gk′s′=(f○g)k′+(k−1)s′,ss′(2) - 一般的网络计算一般的非线性函数,而只有这种形式的层的网络计算非线性滤波器,我们称之为深滤波器或完全卷积网络
- FCN自然地对任何大小的输入进行操作,并产生相应(可能是重新采样的)空间维的输出
- 由FCN组成的实值损失函数定义了一个任务。如果损失函数是最后一层空间维度的和, l ( x ⃗ ; θ ) = ∑ i j l ′ ( x ⃗ i j ; θ ) (3) l(\vec x;\theta)=\sum_{ij} l'(\vec x_{ij};\theta) \tag {3} l(x;θ)=ij∑l′(xij;θ)(3)它的参数梯度将是它的每个空间分量的参数梯度的总和。因此,在整个图像上计算的 l l l的随机梯度下降将与在 l ′ l' l′上计算的随机梯度下降相同,将所有最后一层的感受野作为一个小批量
- 当这些感受野显著重叠时,在整个图像上逐层计算前向和反向传播都要比逐个patch独立计算高效得多
- 接下来,我们将解释如何将分类网络转换为产生粗输出映射的完全卷积网络
3.1 Adapting Classifiers for Dense Prediction
- 典型之前的识别网络,例如LeNet,AlexNet,表面上采取固定规模的输入并产生非空间输出,这些网络的全连接层具有固定的尺寸,不需要空间坐标。然而,全连接层也可以看作是包含覆盖其整个输入区域的内核的卷积。这样做可以将这些网络转换成完全卷积的网络,可以接受任意大小的输入并生成空间输出映射,如图二所示。
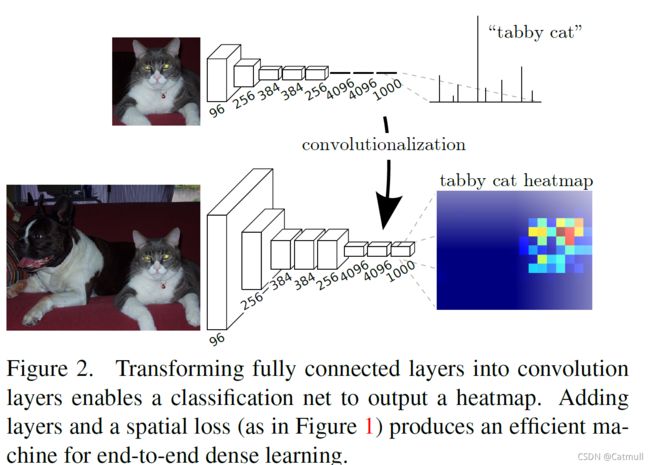
- 此外,虽然生成的map相当于对特定输入patch的原始网络的评估,但计算在这些补丁的重叠区域上得到了高度摊销
- 卷积化模型的空间输出映射使它们成为语义分割等密集问题的自然选择
- 当我们将分类网重新解释为完全卷积时,可以产生对任意大小输入的输出映射,输出维数通常通过下采样来减少。这使这些网络的完全卷积版本的输出变得粗糙,从输入的大小减少一个因子,等于输出单元的感受野的像素步长
3.2 Shift-and-Stitch Is Filter Dilation
- 可以通过粗糙的输出与位移版的输入缝合到一起来得到dense predictions
- 如果输出以 f f f作为因子下采样,将输入向右移动 x x x个像素,向下移动 y y y个像素,一旦对于每个 ( x , y ) (x,y) (x,y)满足 0 ≤ x , y < f 0\leq x,y< f 0≤x,y<f。处理这些 f 2 f^2 f2输入中的每一个,并将输出交织在一起,以便预测与它们的感受野中心的像素相对应
- 考虑一层(卷积或池化),其输入步幅为 s s s,其后的卷积层滤波权重位 f i j f_{ij} fij
- 通过将前一层的输入步幅设置为1,一阴子 s s s上采样它的输出
- 然而,将原始滤波器与上采样输出卷积并不会产生与shift-and-stitch相同的结果,因为原始滤波器只看到其(现在上采样)输入的减少部分
- 为了产生同样的结果,通过形成膨胀(或稀薄)过滤器
f i j ′ = { f i / s , j / s i f s d i v i d e s b o t h i a n d j ; 0 o h e r w i s e (4) f'_{ij}=\left\{ \begin{aligned} f_{i/s,j/s} \quad if\quad s\quad divides \quad both \quad i \quad and\quad j;\\ 0 \quad oherwise \end{aligned} \right. \tag 4 fij′={fi/s,j/sifsdividesbothiandj;0oherwise(4) - 要复制移位-缝合的全部净输出,需要一层一层地重复这个滤波器放大,直到所有的子采样都被移除。(实际上,这可以通过处理上采样输入的下采样版本来有效地完成)
- 简单地减少网络中的子采样是一种权衡:过滤器可以看到更精细的信息,但接收字段更小,计算时间更长。这种膨胀技巧是另一种权衡:在不减少过滤器感受野大小的情况下,输出更密集,但过滤器不能以比其最初设计更细的尺度访问信息。
3.3 Upsampling Is (Fractionally Strided) Convolution
- 另一种连接粗糙输出到密集像素的方法是插值
- 双线性插值从最邻近的4个输入计算每一个输出 y i j y_{ij} yij: y i j = ∑ α , β = 0 1 ∣ 1 − α − { i / f } ∣ ∣ 1 − β − { j / f } ∣ x ⌊ i / f ⌋ + α , ⌊ j / f ⌋ + β (5) y_{ij}=\sum_{\alpha,\beta=0}^1|1-\alpha-\{i/f\}| |1-\beta-\{j/f\}|_{x \lfloor i/f \rfloor+\alpha ,\lfloor j/f \rfloor +\beta}\tag 5 yij=α,β=0∑1∣1−α−{i/f}∣∣1−β−{j/f}∣x⌊i/f⌋+α,⌊j/f⌋+β(5)
- 其中 f f f为上采样因子, { ⋅ } \{·\} {⋅}为分数部分
- 在某种意义上,以 f f f为因子的上采样是一种卷积,这种卷积的分数输入步长是 1 / f 1/f 1/f
- 只要f是整数的,通过反转更典型的输入跨步卷积的前向和后向传递,通过“向后卷积”实现上采样是很自然的。
- 因此,向上采样是在网络中执行的端到端学习通过反向传播从像素级别的损失
- 根据在反卷积网络中的使用,这些(卷积)层有时被称为反卷积层
- 注意,在这样一个层的卷积滤波器不需要固定(例如,双线性上采样),但可以学习
3.4 Patchwise Training Is Loss Sampling
- 在随机优化中,梯度计算是由训练分布驱动的
- 全图像全卷积训练与patchwise训练相同,其中每批包含一张图像(或图像集合)输出单元的所有感受野
- 在patchwise训练中采样可以纠正类不平衡,减轻密集patch块的空间相关性
- 在全卷积训练中,也可以通过加权损失来实现类平衡,损失采样可以用来处理空间相关性
4 SEGMENTATION ARCHITECTURE
- 我们将ILSVRC分类器投射到fcn中,并通过网络内向上采样和像素损失来增强它们的密集预测。
- 通过微调来训练分割
- 接下来,我们在层之间添加skIp,以融合粗糙的、语义的和局部的外观信息
- 学习这种跳过skip是为了细化输出的语义和空间精度
- 在PASCAL VOC上训练并验证
4.1 From Classifier to Dense FCN
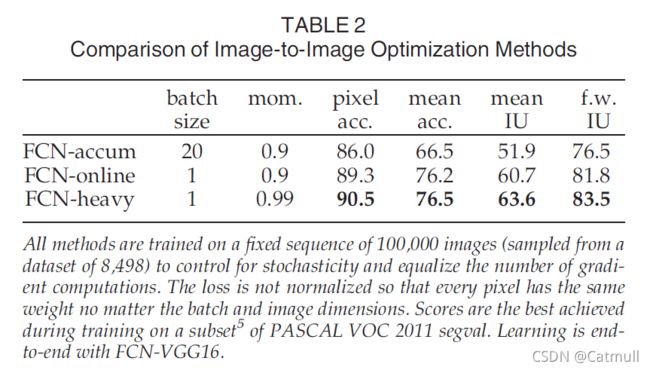
4.2 Image-to-Image Learning
4.3 Combining What and Where
- 虽然完全卷积分类器对语义分割进行了微调,既能识别又能定位,如4.1节所示,但这些网络可以得到改进,以直接使用更浅、更局部的特征

- 我们通过添加融合层输出的跳过来解决这个问题,特别是在预测中包含具有更细步长的浅层。
- 在较浅的层中进行更局部的预测是很自然的,因为它们的感受野更小,看到的像素更少
- 一旦增加了跳跃,网络就会从几个共同和端到端学习的信息流中做出并融合预测
- 结合精细层和粗层可以让模型做出局部预测,尊重全局结构
- 这种层次和分辨率的交叉是一种学习,非线性对应于拉普拉斯金字塔的多尺度表示
- 层融合本质上是一种元素操作.然而,由于重新采样和填充,跨层元素的对应变得复杂。因此,一般来说,要融合的层必须通过缩放和裁剪来对齐.我们通过向上采样较低分辨率的层,将两层带入规模一致,由于填充的原因,裁剪删除了上采样层延伸到其他层以外的任何部分
- 在对层进行空间对齐之后,我们接下来选择一个融合操作。我们通过连接融合功能,然后紧接着通过由 1 × 1 1\times 1 1×1卷积层组成的“得分层”进行分类。
- 我们不是将连接的特性存储在内存中,而是将连接和随后的分类进行交换
- 因此,我们的跳跃是这样实现的:首先对每一层进行1*1卷积融合,执行任何必要的插值和对齐,然后对得分求和。
- 我们也考虑了最大融合,但发现学习由于梯度切换的困难。
- 一旦所有的层被融合,最后的预测然后上采样回到图像分辨率。
- 从pool4中添加一个跳跃,通过从这个步幅的16层得分,使步幅减半
Skip architectures for segmentation
4.4 Experimental Framework
5 RESULTS
Metrics
我们报告了来自常见语义分割和场景解析评估的度量,即像素精度的变形和区域交并比:
令 n i j n_{ij} nij是第 i i i类的像素被预测为第 j j j类的数量,共由 n c l n_{cl} ncl个不同的类,令 t i = ∑ j n i j t_i=\sum _j n_{ij} ti=∑jnij是第 i i i个类的总的像素数
pixel accuracy = ∑ i n i i ∑ i t i (6) \text {pixel accuracy}= {\sum _i n_{ii} \over \sum _i t_i} \tag 6 pixel accuracy=∑iti∑inii(6)
mean accuracy = 1 n c l ∑ i n i i t i (7) \text {mean accuracy}={1 \over n_{cl}} {\sum _i {n_{ii} \over t_i}} \tag 7 mean accuracy=ncl1i∑tinii(7)
mean IU = 1 n c l ∑ i n i i t i + ∑ j n j i − n i i (8) \text {mean IU}={1 \over n_{cl}} {\sum _i {n_{ii} \over t_i+\sum _j {n_{ji}-n_{ii}}}} \tag 8 mean IU=ncl1i∑ti+∑jnji−niinii(8)
frequency weighted IU: ( ∑ k t k ) − 1 ∑ i t i n i i t i + ∑ j n j i − n i i (9) \text {frequency weighted IU:}(\sum _k t_k)^{-1}\ {\sum _i {t_i n_{ii} \over t_i+\sum _j {n_{ji}-n_{ii}}}} \tag 9 frequency weighted IU:(k∑tk)−1 i∑ti+∑jnji−niitinii(9)
- 我们定义了一个跳跃架构,将FCN-VGG16扩展到如图3所示的具有8像素步幅的三流网络
6 ANALYSIS
6.1 Cues
masking
- 在学习过程中屏蔽前景产生的网络能够在不观察被标记类的单个像素的情况下识别对象片段
- 总而言之,这表明,即使决策是由前景像素驱动的,fcn还是会结合上下文
- 为了区分形状的贡献,我们学习了一个限于简单输入前景/背景蒙版的网。这种只有形状的情况下,准确率比只有前景被掩盖时要低,这表明网络有能力学习上下文来提高识别。尽管如此,它惊人地准确。
Background modeling
- 这个结果表明学习一个专门的背景模型来进行语义分割并不是至关重要的
6.2 Momentum and Batch Size
- 在这里,我们详细说明了动量和batch size之间的关系,以激励大量的学习
- 通过将梯度累加计算的更新写成非递归和,我们可以看到momentum和batch size可以近似地权衡,这就提出了替代训练参数。
- 令 g t g_t gt为小批量动量 S G D SGD SGD在时刻 t t t所采取的步骤,
g t = − η ∑ i = 0 k − 1 ▽ θ l ( x k t + i ; θ t − 1 ) + p g t − 1 (10) g_t=-\eta \sum _{i=0}^{k-1} \bigtriangledown _{\theta} l(x_{kt+i};\theta_{t-1})+pg_{t-1} \tag {10} gt=−ηi=0∑k−1▽θl(xkt+i;θt−1)+pgt−1(10) - l ( x ; θ ) l(x;\theta) l(x;θ)是损失函数, p < 1 p<1 p<1是动量, k k k是batch size, η \eta η是学习率
- 将这个递归式扩展为一个具有几何系数的无穷和,得到
g t = − η ∑ s = 0 ∞ ∑ i = 0 k − 1 p s ▽ θ l ( x k ( t − s ) + i ; θ t − s ) (11) g_t=-\eta \sum _{s=0}^ \infty \sum _{i=0}^{k-1} p^s \bigtriangledown _{\theta} l(x_{k(t-s)+i};\theta_{t-s}) \tag {11} gt=−ηs=0∑∞i=0∑k−1ps▽θl(xk(t−s)+i;θt−s)(11) - 换句话说,每个例子都包含在系数 p ⌊ j / k ⌋ p^{\lfloor j/k \rfloor} p⌊j/k⌋的和中,其中指数j将例子从最近考虑到最久考虑的排序
- 如果 p ( 1 / k ) = p ′ ( 1 / k ′ ) p^{(1/k)}=p'^{(1/k')} p(1/k)=p′(1/k′),那么以动量p和batchsize k k k和以动量 p ′ p' p′和batch_size k ′ k' k′学习等效
VGG16
从第0层到第43层为VGG-16不包括全连接层的定义
第1个下采样块:从第0层到第6层 第0-2层为完整的小卷积块
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace=True)
(6): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
第7到13层 第二个下采样块
(7): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(9): ReLU(inplace=True)
(10): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(12): ReLU(inplace=True)
(13): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
共5个下采样块