cs224w 图神经网络学习笔记 2-3
cs224w 2-3 Traditional Feature-based Methods-Graph
图层级
我们要用什么方式来表示图的结构呢?我们下面将介绍图的特征描述的描述符号,以便我们进行特征描述;
Kernel Methods(核方法)

核方法 被广泛应用于解决图层级的预测的传统的机器学习;
思想:设计 内核来代替特征向量;
简单介绍一下Kernel:
1.两个图的核 K ( G , G , ) K(G, G^,) K(G,G,),衡量两个数据图之间的相似性;
2.核矩阵 K = ( K ( G , G , ) ) G , G , K=(K(G, G^,))_{G,G^,} K=(K(G,G,))G,G,必须是半正定矩阵;(为了让核成为有效核,不太明白)
3.存在一个特征表示 Φ ( ∗ ) \Phi(*) Φ(∗),使得 K ( G , G , ) = ϕ ( G ) ϕ ( G , ) K(G, G^,)=\phi(G)\phi(G^,) K(G,G,)=ϕ(G)ϕ(G,), K ( G , G , ) K(G, G^,) K(G,G,)也仅仅是两个特征表示的点乘; Φ ( ∗ ) \Phi(*) Φ(∗)是个表示向量,甚至不需要背显示的计算出来;
4.创造完核,用现成的方法(如SVM),来进行图层级的任务;

核方法种类:主要是 Graphlet Kernels 和 Weisferler-Lehman Kernel 两种内核,还提到了随机游走内核、最短距离内核等

主要思想:
核的关键在于定义给定的图的特征向量 Φ ( G ) \Phi(G) Φ(G)
Bag-of-Words(BoW)表示将一个文档表示成一个向量,每个元素代表对应的word出现的次数(以字母表为顺序);
这里讲的Bag-of-Something也是类似的特征抽取方法,也是向量,然后每个元素代表对应的something出现的次数(这个something可以是node, degree, graphlet, color)

光用node,我们可以发现两个图的向量相同,不足以区分这两个图,此时可以设置一个node-degrees,用Bag-of-degrees来表示图特征;(第一个小图应该是(1,2,1),右下角节点的度应该是3)
Graphlet Kernels
主要思想:计算图中不同graphlet的数量;
需要注意的是我们这里定义的graphlet与节点层级的graphlet不同:
1.图中的节点不需要连接(允许独立的节点)
2.图没有根这个说法
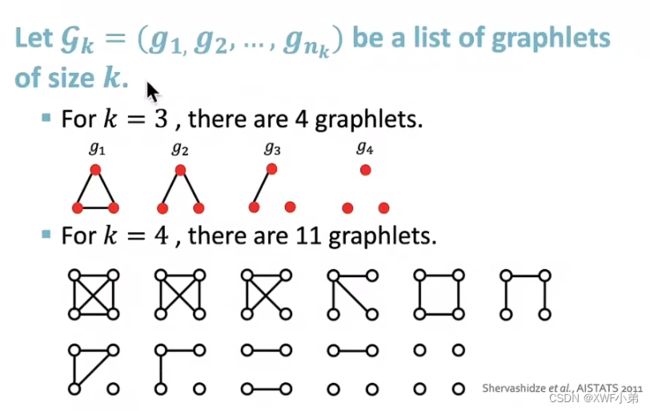
举个例子:

f G = ( 1 , 3 , 6 , 0 ) T f_G=(1,3,6,0)^T fG=(1,3,6,0)T

给定两个图,计算他们的乘积,但他们的Size大小不一定相等,我们要归一化图的大小和密度 h G h_G hG,并将内核定义成他们的乘积;
但Graphlet Kernel有一个限制就是它的计算过于昂贵了;(指数级爆炸)
Weisferler-Lehman Kernel
为了更高效的计算,我们 采取另一种核方法;
主要思想:利用节点的邻域结构来扩充节点信息;
 我们采用颜色优化Color refinement这个算法来实现:
我们采用颜色优化Color refinement这个算法来实现:

1.给定一个具有V节点的图G;
2.分配初始颜色给节点 c ( 0 ) c^{(0)} c(0);(参考其他博客:这个颜色也可以按照节点度数之类的来分配,可能比较随意)
3.我们将通过聚合或者扩散邻居颜色来给定节点新的颜色;
4.经过K步的色彩优化之后 c ( k ) ( v ) c^{(k)}(v) c(k)(v),总结了K跳邻居的结构;
举个例子:
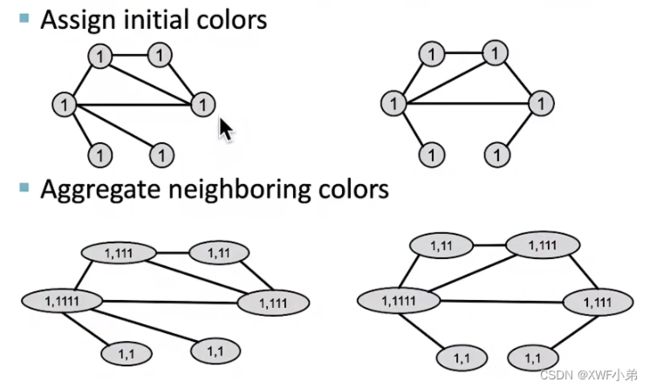
1.给定了结构相似但不同的两个图;
2.开始给定所有节点都分配颜色1;
3.之后我们将汇聚邻居节点的颜色,并用Hash函数表达出来;
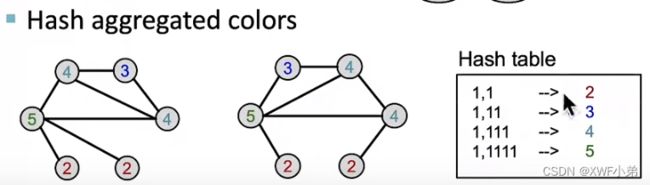
4.重复3进行迭代;

迭代K次之后:
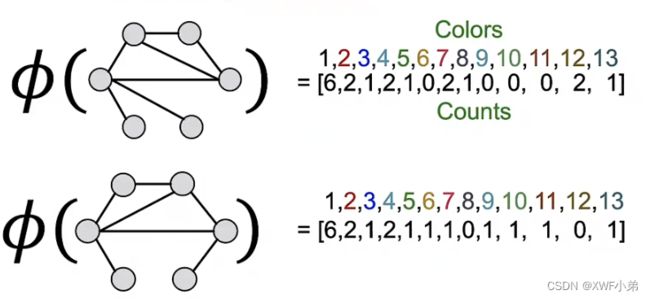
迭代过程中每个颜色出现的次数;第一张图最后三个数应该是2,1,0;
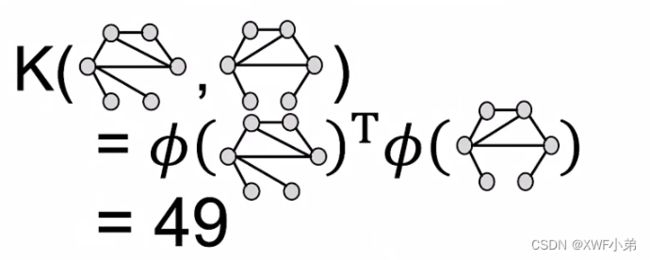
由于上面错了,所以这里应该也是错的,正确为50;
Weisferler-Lehman Kernel计算成本比较低,表现好,快速实际且有效;