具有编译功能支持无限大数计算器的实现

本篇是MathAssist的第三篇，将在上篇所实现的BigNumber基础上完成具有编译功能支持无限大数的计算器SuperCalculator。

要想从形如 "(1.23435+sin(0.5*180/PI))*2468.2345" 字符串格式的表达式中求值，需要使用编译原理的知识，不过在一般的《数据结构》课程中都会讲解基础的表达式求值问题，而本篇也是在数据结构课程的基础上稍加拓展而实现。

多叉树的节点类型

node继承体系

表达式的值，一般将其转化成二叉树结构，根节点表示操作符，子节点表示操作符所使用到的分量。
比如上面的表达式表示成二叉树如图所示：

如图所示，加乘除的操作数都是两个，而sin只需要一个操作数，所以其子节点只有一个。而如果要支持不限参数个数的函数，就必须有两个以上的节点，所以SuperCalculator中所使用的是多叉数。
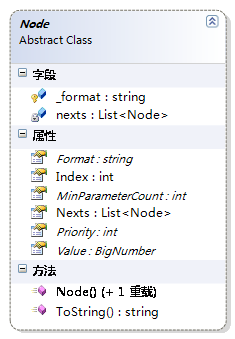
先看所有节点类型的根类型Node

• Format表示此节点的字符串表示，如果是sin节点此值即为"sin"，乘法节点此值即为"*"
• Index 表示此节点的首字符在字符串表达式中的索引，主要是用在错误定位上。
• MinParameterCount 因为现在操作符子节点的个数不定，所以要定义一个最小所需的操作个数，如果小于这个数后就是不合法的表达式
• Nexts 此节点所有的子节点。这个类型是List<Node>就是用于存储不定个数的操作数。
• Priority 表示节点在优先级，主要用在构建多叉树时，优先级越高的节点这个值越大。比如数字节点是6，函数节点是5，乘除是4，加减是2
• Value 计算此节点时最后的值。

下面再看Node及其子类的继承体系。

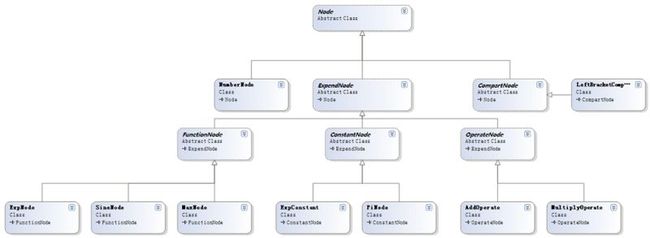
直接从Node继承的类有三个:NumberNode(纯数字节点), ExpandNode(可拓展节点), CompartNode(间隔节点)
其中CompartNode，表示括号之类节点，只在词法分析中用到，不会出现在树形中

ExpandNode的直接子类有三个:FunctionNode(函数节点),ConstantNode(常量节点), OperateNode(操作符节点)

• FunctionNode 所有的函数节点都以此类为父节点，比如sin, max, exp等
• ConstantNode PI, e等常量节点的父节点
• OperateNode 加减乘除等节点的父节点

其中节点中所有的数字类型都是用BigNumber来表示。

用反射机制来查找所有可用的拓展节点

如下所示的代码，将项目中所有从ConstantNode,FunctionNode,OperateNode中继承而来的子类，先实例化后再存储到对应的List<T>中，这样在构建多叉树时用这些List<T>中的对象的Format进行字符串查找即可判断对应的类型。

        internal static void Find(List<ConstantNode> constants, List<FunctionNode> functions, List<OperateNode> operates) {
            Assembly ass = Assembly.GetExecutingAssembly();
            Module[] modes = ass.GetModules();
            Type[] typs;

            foreach (Module m in modes) {
                typs = m.GetTypes();

                foreach (Type typ in typs) {

                    if (typ.IsSubclassOf(typeof(ConstantNode))) {
                        constants.Add(ass.CreateInstance(typ.FullName) as ConstantNode);
                    } else if (typ.IsSubclassOf(typeof(FunctionNode))) {
                        functions.Add(ass.CreateInstance(typ.FullName) as FunctionNode);
                    } else if (typ.IsSubclassOf(typeof(OperateNode))) {
                        operates.Add(ass.CreateInstance(typ.FullName) as OperateNode);
                    }
                }
            }
        }

ReflectWord.FInd

使用反射机制后就非常方便添加新的函数或操作符了。比如现在项目中只实现了Max函数，如果要实现Min函数，只需要添加一个MinNode类，重写Format属性返回"min"，重写Value属性求出List<Node>中的最小值即可。将这个类实现后，反射机制将自动添加min函数了。

语法分析、构建多叉树

Expression表达式类

Exression 用于接受一个字符串类型的表达式，并计算出值。其结构如图所示:

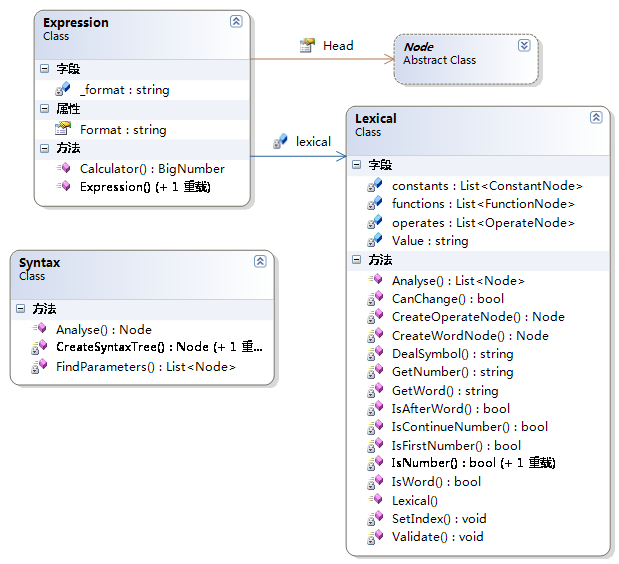
从图中可以看出词法分析在Lexcial类中，语法分析在Syntax.cs类中。
其中Lexical.Analyse()函数负责将string value格式的字符串表达式转化成List<Node>格式的表示式。然后Syntax.Analyse(List<Node> nodes)负责将中序表达式转化成多叉树，最后只返回一个根节点Node

词法分析

词法分析的过程，就是字符串的各种比较。

1. 先过滤过空格回车，
2. 是否为字母，那么就有可能是常量节点或者函数节点，就在之前用反射获取的节点List<Node>中查找是否有对应的字符串
3. 是否为数字
4. 是否为左右括号
5. 是否为"," ，函数中的多个参数是用逗号进行分隔。
6. 是否为操作符节点
7. ...

具体细节见代码吧

语法分析

从中序从构建多叉树的经典算法“数据结构”中都应该有讲到，即先将中序转化为后序或前序(本文转化成后序)，然后再将后序转化成多叉树。
Syntax.cs中有四个静态函数:

• Node Analyse(List<Node> nodes); 对外接口，将中序的参数转化成多叉树，返回根节点。
• Node CreateSyntaxTree(List<Node> nodes, int first, int end); //nodes全部的中序结构，[first,end]表示要将中序结构中的哪一部分转化成树形。
• Node CreateSyntaxTree(List<Node> after)  // 这个方法的参数已经是后序形式，没有括号，函数的参数也合并到函数的子节点后，所以这里就是“数据结构”课程中最经典的，使用一个栈将后序转化成树。
• List<Node> FindParameters(List<Node> nodes, int start, ref int end) 在函数的括号中,找到参数,这些参数用逗号分开，返回所以的参数。start指向左括号的位置，end返回函数的右括号。这个函数中可能会递归调用到CreateSyntaxTree()，因为参数也有可能是复杂的表示式。

下面详细介绍 CreateSyntaxTree(List<Node> nodes, int first, int end)——

这个函数中遍历nodes，对每个节点先判断

• 是否为数字节点或常量节点，如果是则添加到后序列表中。
• 如果为左括号，则把左括号添加到栈
• 如果为右括号，则一直弹出栈中元素，直到遇到栈中的左括号
• 如果是函数节点，则使用下面的FindParameters函数将所有参数添加到这个节点的子节点中后，再将这个节点添加到后序
• 如果是操作符节点，先看栈中有先元素，如果没有元素直接把操作符放到栈中，如果有元素，则比较栈最后一个节点和此节点的优先级，如果栈中优先级高则弹出栈节点放到后序，并把此节点放入栈，否则将此节点放入栈。

上面这个过程也是数据结构中的经典算法。

得到正确的树型后，就只需要简单地调用Head.Value即可引爆多叉树的求值过程(四年前本人是使用属性，其实现在看来用函数更合理一些)。

结束语

最后提供程序的exe和全部源码。

SuperCalculator_exe http://files.cnblogs.com/files/xiangism/SuperCalculator_exe.rar

SuperCalculator http://files.cnblogs.com/files/xiangism/SuperCalculator.rar

 

exe中在控制台直接输入想要计算的表达式，然后回车即可看到结果。

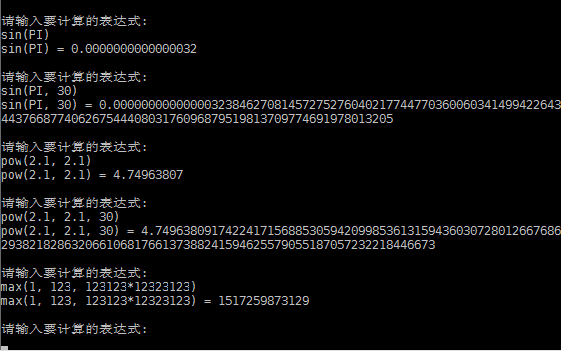
补充:sin,pow之类的函数因为精度的需要，所以在正常函数的基础上添加了一个表示精度的可选参数。

sin(PI) = 0.0000000000000032
sin(PI, 30) = 0.0000000000000032384627081457275276040217744770360060341499422643 44376687740626754440803176096879519813709774691978013205

pow(2.1, 2.1) = 4.74963807
pow(2.1, 2.1, 30) = 4.7496380917422417156885305942099853613159436030728012667686 29382182863206610681766137388241594625579055187057232218446673