基于遗传算法的BP神经网络优化（论文加源码）

（本文绝对是干货，但是论文部分太过于详细了。如果你对遗传算法比较熟悉，可以直接看源代码。）

1 模型分析

1.1 提出问题

神经网络是一种模拟人类大脑思维方式的智能算法模型， 通过对大量数据的学习找出其中的规律， 对于解决非线性问题提供了一种有力工具。但神经网络的最终效果受到权值和阈值的影响，只有适当地调整、优化，才能充分释放网络性能。本文中，我们希望通过固定网络的拓扑结构，对BP神经网络的权值和阈值进行优化。

1.2 优化目标

优化目标可用如下公式表达

式中， ,分别表示权值和阈值， Ω表示权值和阈值的取值空间， 是第个样本的输出， 是网络的输出。
该公式称为神经网络的损失函数，因此我们的优化目标即通过优化权值和阈值，使损失函数尽可能得小。

1.3 模型的复杂性根源

BP神经网络的训练问题是一个高维、多峰连续函数的优化问题，即在权值空间的误差曲面上搜索最低点，其复杂性主要体现在以下三个方面。

1.4 传统方法存在的不足

BP算法是训练前馈型神经网络常采用的方法，存在着以下两个不足：

• BP算法的初始解是随机产生的，初始解的好坏对算法性能影响很大，因此算法存在着不稳定的因素。
• BP算法采用梯度下降法确定搜索方向，由于搜索空间存在平坦区域和多个极小值点，该算法极容易出现收敛速度很慢或者因陷入局部极小值而无法收敛的情况。

下图为用BP算法优化神经网络时均方误差的变化情况。可以看出神经网络过几轮训练后就陷入某个局部极小点而不能自拔，从而使训练无法收敛于给定误差，并且多次无效的训练浪费了计算资源。

1.5 遗传算法的优势

• 遗传算法有较强的自适应性：在迭代过程中不需要用到梯度等问题信息，不存在平坦区的问题，并且可以利用选择算子将陷入局部极小值的模型淘汰。
• 遗传算法具有优良的全局搜索性能：一个种群中有多个个体，它们并性地进行全局搜索，确保最终能找到最优模型。

利用遗传算法得到最优网络权值及阈值作为后续神经网络模型的初始网络权值及阈值， 这样不仅可克服传统 BP 神经网络易陷入局部最小值的缺陷， 还可大大提高模型评价的精度！

本文将这种用遗传算法找到的最优解作为BP算法的初始解并继续迭代的算法称为GABP算法。

2 算法设计

2.1 算法概述

流程图如下：

2.2 算法要素

2.2.1 编码

考虑输入结点为、隐含结点为、输出结点为的神经网络，其中输入层到隐含层的权值矩阵为W，隐含层的阀值矩阵为，隐含层到输出层的权值矩阵为V，输出层的阀值矩阵为ℎ。

需要考虑的问题：

• 权值矩阵是二维的，而染色体是一维的
• 权值和阈值有多个，而一个染色体只能有一条

对应的解决方案：

• 将二维的权值矩阵映射成一维
• 将多个权值和阈值拼接形成染色体

其实质就是用实数串编码！

2.2.2 适应度函数

适应度函数fitness定义为

式子中

2.2.3 种群初始化

• 随机生成N个个体作为初始种群。
• 个体的权值阈值的初始化： 用均匀分布的方法，选择基因值的上界和下界，并在这个范围内生成均匀分布的随机数，优点是可以调节解的范围。

2.2.4 选择

采用轮盘赌选择法对群体的染色体进行选择，产生规模同样为N的种群。 选出的个体的平均适应度较高，但是会有重复的个体 ，而重复的个体的交叉是没有意义的，因此在选择的过程中还要筛除重复个体。

2.2.5 交叉

假设有两条长度为的染色体和，采用实数交叉法对染色体进行交叉

其中是[0，1]之间的随机数，=1,2,…
这种方法的优点：

• 杂交后的基因值是父代基因值的凸组合，从而充分融合了父代个体的基因
• 的引入增加了个体的多样性，增强算法的局部搜索能力，有利于算法在迭代过程中开发出最优的融合比例

2.2.6 变异

当变异算子以一定概率对某个体的第 个基因发生变异时,变异操作为

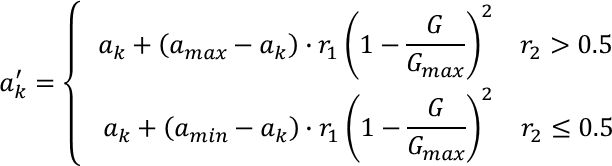
其中和分别是基因值的上下界，是当前迭代次数，_是最大迭代次数， 1 和2 是[0，1]之间的随机数。

这种操作方式的优点是：

1. 随机数1影响变异程度
2. 2>0.5时基因值往最大值靠拢， 2≤0.5时基因值往最小值靠拢，保证基因值以均等的概率增大或减小 基因的上下界保证基因值不会变化太大
3. 实现自适应调整变异程度，兼顾算法的全局和局部的均衡搜索能力，在算法运行初期初期变异程度较大，保证全局搜索能力较强，而随着迭代次数增加，变异程度不断减小，保证局部搜索能力，促使个体收敛到全局最优解。

为了在迭代初期增强全局搜索能力，迭代后期增强局部搜索能力，我们还可以采用自适应调整变异位数的方法，公式为：

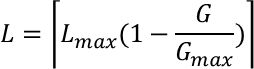
其中 ⌈∙⌉表示向上取整， 是预先设定的最大变异位数。

2.2.7 种群更新

轮盘赌方法：种群中的个体被选中的概率与个体相应的适应度函数的值成正比。编程时需要将种群中所有个体的适应度值进行累加然后归一化。
为了防止种群在迭代过程中产生的好解因交叉和变异而被迅速破坏，可采用精英策略，即在种群之外单独保留全局最优个体。

2.2.8 终止条件

1.事先规定出一个最大的进化步数(迭代轮数)，到达此步数时终止。
2.判断当前最好的解已连续若干步没有变化或变化很小，即逐渐收敛到一个目标函数值。
3.算法已找到了一个可接受的最好解，达到目的后不必继续计算。

2.3 参数选取

2.3.1 隐层神经元数量

若隐层节点数太少，网络可能根本不能训练或网络性能很差；若隐层节点数太多，虽然可使网络的系统误差减小，但一方面使网络训练时间延长，另一方面，训练容易陷入局部极小点而得不到最优点，也是训练时出现“过拟合”的内在原因。
隐层节点数不仅与输入/输出层的节点数有关，更与需解决的问题的复杂程度和转换函数的型式以及样本数据的特性等因素有关。具体的选取策略有两种：

1. 根据经验选取并根据效果调整。
2. 用经验公式计算：
   
   其中和是输出和输出的个数，是取1~10之间的随机整数。

2.3.2 种群规模

种群太小，则不能提供足够的采样点，以致算法性能很差；种群太大，尽管可以增加优化信息，阻止早熟收敛的发生，但无疑会增加计算量，造成收敛时间太长，表现为收敛速度缓慢。根据经验，种群规模一般选在20到100之间。

2.3.4 交叉、变异概率

交叉概率（Pc)越大，新个体产生的速度越快。但是Pc过大，遗传模式被破坏的可能性很大，容易使得具有高适应度的个体结构被破坏。如果交叉概率过小，会导致搜索过程缓慢，甚至停滞不前。
变异操作是对种群模式的扰动，有利于增加种群的多样性 。变异概率（Pm)如果取值过小，会导致不易产生新的个体结构，如果取值过大，算法就变成了纯粹的随机搜索。
根据经验，交叉概率(Pc)一般选为0.4~0.99到之间的数，变异概率(Pm)一般选为0.0001到0.1之间。

2.3.5 遗传代数

遗传代数太小，算法不容易收敛，种群还没有成熟；遗传代数太大，算法已经收敛，或者种群归于早熟不可能再收敛，继续进化没有意义，浪费时间和计算资源。根据经验，遗传代数一般选择在100到500代较为合适。

2.3.6 评价指标

平均绝对值误差：

3 实验结果

3.1 拟合函数

用函数(,)=2^2+sin(+/4)，,∈(−2,2)生成数据集。

数据的产生和处理方法：在(−2,2)之间产生1000个随机数对作为输入，通过函数表达式计算出输出，从而产生数据集；将数据进行归一化处理，其中输入归一化至[-1，1]，输出归一化至[0,1]；将数据集按9:1划分为训练集和测试集。
通过实验比较，最终选择种群规模为100，最大迭代次数为1000次，交叉概率为0.8，变异概率为0.1，基因值的上界为15，下界为-15，最大变异位数为10。

实验结果对比：用测试集测试，在同等迭代次数（300次）的条件下，比较GABP算法和BP算法散点图和平均绝对误差。

拟合得到的函数图像为：

结论：遗传算法找到的最优解明显优于随机产生的初始解，GABP算法不仅能减少网络的收敛次数，减少网络的训练时间，还降低了总体误差， 改善了 BP 网络易陷入局部极值和收敛速度慢的缺点。

3.2 用“泰坦尼克号生存预测”数据集测试网络

训练集的内容：一共891条记录，记录了乘客编号(Passenger ID)、乘客票务舱(Pclass)、乘客姓名(Name)、性别(Sex)、年龄(Age)、船上兄弟姐妹个数(SibSp)、船上父母小孩个数(Parch)、船票信息(Ticket)、票价(Fare)、客舱(Cabin)、登船港口(Embarke)和是否存活(Survived)。
测试及内容：一共418条记录，有除了“是否存活”以外的其它款项。
预计实现的目标：通过对训练集的记录进行学习，从而对测试集的人员进行“生死预测”，期望达到较高的预测正确率。
神经网络的训练目标：采用Pclass、Sex、Age、SibSp、Parch五项作为输入量，Survived作为输出量，经过训练集的训练，能够得到足够好的神经网络，使得在给定信息的情况下，预测生死的正确率高。

结果：经典的BP算法在训练500轮后，平均误差能达到0.065，对训练集中人员预测生死的成功率平均为82%；GABP在训练50（BP迭代）*10（选择变异）轮后，对训练集中人员预测生死的成功率平均为83%。

kaggle官网给出的GABP和BP对测试集的人员预测生死的正确率。

4 源程序

以下程序全部都是用python写的。

4.1 拟合函数源代码

首先是主函数gabp.py。

"""
主程序部分，用给定函数产生数据集，并用GABP算法对神经网络的权值进行优化，即：
先用遗传算法对神经网络的权值进行优化，
得到的最优个体作为BP算法的初始解，
再利用BP算法对神经网络进一步优化。
注：为了避免一次性输出太多图像，部分代码改为注释，将代码的注释去掉，可以正常输出相应图像
"""

import numpy as np
import matplotlib.pyplot as plt
from math import pi
import math
import random

from selection import select
from crossover import cross
from mutation import mutate
import copy
from bpalgorithm import BP
from plot_standard import plot_standardimage
from plot_fitting import plot_fittingimage

##超参数
popsize =100  #种群规模
Gmax = 1000    #最大迭代次数
pc=0.8        #交叉概率
pm=0.1        #变异概率
amax = 15     #染色体基因值的上界
amin = -15    #基因值下界

inputnum , outputnum = 2, 1  # 输入神经元，输出神经元个数

#根据经验选择隐层节点数
hiddennum =10
print(hiddennum)

num = 1000  # 数据总数
trainnum =int(0.9*num)  #其中十分之九用于训练
testnum =int(0.1*num)  #其中十分之一用于测试

# 用函数f(x)=2*x*x+sin(y+pi/4)生成数据集，其中自变量x，y的取值范围是(-2π，2π)
input_data = np.random.uniform(low=-2 * pi, high=2 * pi, size=[num, 2])  # 第一列作为x，第二列作为y
output_data = 2 * np.multiply(input_data[:, 0], input_data[:, 0]) + np.sin(input_data[:, 1] + pi / 4)

# 归一化处理,将输入的范围调整到-1到1之间,输出范围调整到0到1之间
output_max = np.max(output_data)
output_min = np.min(output_data)

input_datan = input_data / (2 * pi)
output_datan = (output_data - output_min) / (output_max - output_min)

# 9:1的比例划分训练集和测试集
input_train = input_datan[0:int(0.9 * num) , :]
input_test = input_datan[int(0.9 * num):num , :]
out_train = output_datan[0:int(0.9 * num) ]
out_test = output_data[int(0.9 * num):num ]    #测试输出不需要归一化

#对染色体进行解码得到权值和阈值
def decode(chrom):
    # 输入层到隐层的权值
    w_hide = chrom[:inputnum * hiddennum].reshape(inputnum, hiddennum)
    # 隐层神经元的阈值
    bias_hide = chrom[inputnum * hiddennum: inputnum * hiddennum + hiddennum]
    # 隐层到输出层的权值
    w_out = chrom[inputnum * hiddennum + hiddennum: inputnum * hiddennum + hiddennum + hiddennum * outputnum] \
        .reshape(hiddennum, outputnum)
    # 输出层的权值
    bias_out = chrom[inputnum * hiddennum + hiddennum + hiddennum * outputnum:]
    return w_hide , bias_hide , w_out , bias_out

# 定义个体类，可以调用方法直接计算个体的适应度
class indivdual:
    def __init__(self):
        self.L = inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum #编码长度
        self.chrom = np.zeros(self.L, np.float)  # 染色体初始化
        self.fitness = 0  # 适应度初始化

    #适应度计算
    def fit(self):
        w_hide, bias_hide, w_out, bias_out =decode(self.chrom)
        hide_in = np.matmul(input_train , w_hide)
        hide_out = 1 / (1 + np.exp(-(hide_in - bias_hide)))
        out_in = np.matmul(hide_out, w_out)
        y = 1 / (1 + np.exp(-(out_in - bias_out)))  #网络实际输出
        y = y.reshape(1,-1)   #列向量转成行向量
        cost = np.abs(y - out_train)
        sumcost = np.sum(cost)     #损失函数
        fitness = 1/sumcost        #取损失函数的倒数作为适应度`
        return fitness

# 初始化种群
def initPopulation(pop , popsize):
    #pop : 种群
    #popsize : 种群大小

    for i in range(popsize):
        ind = indivdual()
        ind.chrom = copy.deepcopy(np.random.uniform(low=amin, high=amax, size=ind.L))  #对每个个体的权值和阈值进行初始化
        #ind.chrom = np.ones(ind.L)*i
        pop.append(ind)

# 寻找种群中的最优个体
def findbest(pop):
    fit_list = [ind.fit() for ind in pop]
    bestindex = fit_list.index(max(fit_list))
    return pop[bestindex]

#以散点图的形式画出神经网络的预测结果，同时计算平均绝对误差
def picture(w_hide , bias_hide , w_out , bias_out , str):
    #MAD : 平均绝对误差
    #output : 神经网络得到的输出
    #outputun : 反归一化后的输出
    #str : 区别GA和BPGA的字符串
    output = []
    for m in range(testnum):
        hide_in=np.matmul(input_test[m], w_hide)
        hide_out=(1/(1+(np.exp(-hide_in+bias_hide))))
        out_in=np.matmul(hide_out, w_out)
        c= 1/(1+(np.exp(-out_in+bias_out)))
        output.append(c[0])
    #计算误差
    outputun = (output_max - output_min)*np.array(output) + output_min  #反归一化
    MAD = np.sum(abs(outputun-out_test))/testnum
    print("\n"+str+"算法测试的平均绝对误差为：",MAD)
    if str == "GA":
        plot_standardimage()   #做出标准函数图像
    #作散点图
    plt.ion()
    ax = plt.axes(projection='3d')
    ax.scatter3D(2*pi*input_test[:, 0], 2*pi*input_test[:, 1], outputun, 'binary')
    plt.title("The test result of " + str+"\nTurn off automatically after 5 seconds")
    plt.pause(5)  # 显示5秒，5秒后自动关闭并继续运行
    plt.close()

#主程序
pop = []
initPopulation(pop,popsize)

#精英策略，保留全局最优个体
ind_best_global = findbest(pop)
best_fit_iteration = []
best_fit_iteration.append(ind_best_global.fit())

for G in range(1,Gmax+1):
    print("--------------第"+str(G)+"次迭代--------------")
    pop = select(pop)
    pop = cross(pop,pc)
    mutate(pop,pm,amax,amin,G,Gmax)
    ind_best_now = findbest(pop)
    if ind_best_now.fit() > ind_best_global.fit():
        ind_best_global = copy.deepcopy(ind_best_now)
    print("当前最优适应度：",ind_best_now.fit())
    print("全局最优适应度：",ind_best_global.fit())
    best_fit_iteration.append(ind_best_global.fit())

w_hide , bias_hide , w_out , bias_out =decode(ind_best_global.chrom)

picture(w_hide , bias_hide , w_out , bias_out,"GA")

print("BP算法迭代中……")
#BP函数中权值数组的形状与主程序定义的数组形状互为转置
# 因此传入参数前需要将两个权值数组转置

w_hide_bp, bias_hide_bp, w_out_bp, bias_out_bp = BP(input_train, out_train, w_hide.transpose(), bias_hide, w_out.transpose()[0], bias_out, hiddennum, trainnum)

picture(w_hide_bp.transpose(), bias_hide_bp, w_out_bp.transpose(), bias_out_bp,"GABP")

#print("\n画出拟合得到的函数图像，请稍候……")
#plot_fittingimage(w_hide_bp.transpose(), bias_hide_bp, w_out_bp.transpose(), bias_out_bp,output_max,output_min,"GABP")

接着是交叉函数crossover.py

"""
交叉：按照概率Pc从selcet函数选出的种群中选择染色体进行交配
具体过程为：
（1）从区间[1，N]中随机产生两个整数a,b
（2）对父代个体sa和sb进行算术杂交，得到两个子代个体
（3）重复上述过程，直到得到N个子个体
"""
import random
import  numpy as np
import copy

def cross(pop,pc):
    #pop : 原种群
    #newpop : 交叉后产生的新种群
    #pc : 交叉概率
    #t ： 交叉次数
    t = 0
    newpop = copy.deepcopy(pop)  #初始化
    while t <= len(pop):
        rd = random.uniform(0,1)
        if rd>pc:   #不交叉
            t += 1
        else:       #交叉
            flag = 0
            while flag == 0:
                a = random.randint(0,len(pop)-1)
                b = random.randint(a,len(pop)-1)
                # print(pop[a].chrom,pop[b].chrom)
                if any(pop[a].chrom != pop[b].chrom):  #只有父代的染色体不同时，交叉才有意义
                    crosspoint = random.sample(range(0,pop[0].L),2)    #交叉点
                    startpoint = min(crosspoint)     #交叉起点
                    endpoint = max(crosspoint)      #交叉终点
                    F = random.uniform(0,1)
                    newpop[b].chrom[startpoint:endpoint] = copy.deepcopy(F*pop[a].chrom[startpoint:endpoint]) + copy.deepcopy((1-F)*pop[b].chrom[startpoint:endpoint])
                    newpop[a].chrom[startpoint:endpoint] = copy.deepcopy(F*pop[b].chrom[startpoint:endpoint]) + copy.deepcopy((1-F)*pop[a].chrom[startpoint:endpoint])
                    flag = 1
            t += 1
    return copy.deepcopy(newpop)

然后是选择函数selection.py。

"""
选择：
用轮盘赌法从原种群中选出一些个体组成新种群
保证新种群和原种群的个体数相等
"""
import random
import copy

def select(pop):
    #pop : 原种群
    #newpop : 新种群
    #p : 每个染色体被选择的概率
    #sump : 赌盘，存放每个染色体的累积选择概率

    sump = []
    fit_list = [ind.fit() for ind in pop]
    sumfit = sum(fit_list)
    sump.append(0)

    #构造赌盘
    s = 0  #累加变量
    for i in range(0,len(pop)):
        p = fit_list[i]/sumfit
        s += p
        sump.append(s)
    #选出新种群
    newpop = []
    for j in range(len(pop)):
        rd = random.uniform(0,1)
        for k in range(len(sump)-1):
            if sump[k] <= rd and rd < sump[k+1]:
                newpop.append(copy.deepcopy(pop[k]))


    return copy.deepcopy(newpop)

变异函数mutation.py（画标准图像）。

"""
变异：
种群的每个个体基因变异的概率为pm
根据当前迭代次数确定基因变异的位数:随着迭代次数增大，变异位数减小
"""
import math
import random
import copy

def mutate(pop,pm,amax,amin,G,Gmax):
    #pop : 原种群
    #newpop : 新种群
    #pm : 变异概率
    #amax : 基因变异的上界值
    #amin : 基因变异的下界值
    #G : 当前迭代次数
    #Gmax : 最大迭代次数
    #t ： 变异位数
    Lmax = 10
    t = math.ceil(Lmax*(1-G/Gmax))    #确定变异位数
    for i in range(len(pop)):
        ind = pop[i]
        rd = random.uniform(0,1)
        if rd < pm:    # 变异
            positions = random.sample(range(0,ind.L),t)    #随机选出变异的位置
            for position in positions:
                r = random.uniform(0,1)           #r控制增大或者减小的步长
                if random.uniform(0,1) > 0.5:     #基因值以相等的概率增大或减小
                    ind.chrom[position] = ind.chrom[position] + r*(amax - ind.chrom[position])*(1-G/Gmax)
                else:
                    ind.chrom[position] = ind.chrom[position] + r * (amin - ind.chrom[position] ) * (1 - G / Gmax)
        pop[i] = ind

画图函数plot_standard.py。

"""
做出标准的函数图像，方便与测试结果对比
"""

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from pylab import mpl
from math import pi

def plot_standardimage():
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    plt.ion()
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    x = np.linspace(-2 * pi, 2 * pi, 2000)
    y = np.linspace(-2 * pi, 2 * pi, 2000)
    # 产生隔点矩阵
    x, y = np.meshgrid(x, y)
    z = 2 * x * x + np.sin(y + pi / 4)
    ax.plot_surface(x, y, z)
    plt.title("The standard function image\nTurn off automatically after 3 seconds")
    plt.pause(3)  # 显示5秒，5秒后自动关闭并继续运行
    plt.close()

if __name__=="__main__":
    plot_standardimage()

画图函数plot_fitting.py（画拟合得到的图像）。

"""
做出拟合得到的函数图像
"""

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from pylab import mpl
from math import pi

def plot_fittingimage(w_hide , bias_hide , w_out , bias_out, output_max, output_min, str):
    N = 500 #点的密度
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    x = np.linspace(-1, 1, N)
    y = np.linspace(-1, 1, N)
    # 产生隔点矩阵
    x, y = np.meshgrid(x, y)
    z = np.zeros((N,N),np.float)
    for i in range(N):
        for j in range(N):
            input = np.array([x[i][j],y[i][j]])
            hide_in = np.matmul(input, w_hide)
            hide_out = (1 / (1 + (np.exp(-hide_in + bias_hide))))
            out_in = np.matmul(hide_out, w_out)
            z[i][j] = 1 / (1 + (np.exp(-out_in + bias_out)))
            z[i][j] = (output_max - output_min)*z[i][j] + output_min   #反归一化
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    ax.plot_surface(2 * pi*x, 2 * pi*y, z)    #x,y需要反归一化到（-2π，2π）之间
    plt.title("The fitting function image by "+str)
    plt.show()

bp算法bpalgorithm.py。

"""
用BP算法（即梯度下降法）对神经网络进行训练
当总误差小于设定值或者训练代数大于设定值代时停止训练
单独运行该程序，则可以测试BP算法训练神经网络的效果；
在myga_bp.py导入该程序，则用于测试遗传算法+BP算法（GABP）训练神经网络的效果
注：为了避免一次性输出太多图像，部分代码改为注释，将代码的注释去掉，可以正常输出相应图像
"""
import matplotlib.pyplot as plt
import numpy as np
import random
import pandas as pd
import math
from math import pi
from plot_standard import plot_standardimage
from plot_fitting import plot_fittingimage

def sg(x):  # sigmoid函数定义
    return 1 / (1 + np.exp(-x))

#用BP算法训练网络的函数
def BP(input_train, out_train, w_hide, bias_hide, w_out, bias_out, hiddennum, trainnum):
    #重要变量和参数说明：
    #M : 训练轮次计数器
    #Eaverage : 平均绝对误差
    #step ：训练步长
    #iternum_max : 最大迭代次数
    #Eaverage_min : 最小可接受误差za
    step = 1
    iternum_max = 300
    Eaverage_min = 0.01
    M = 0
    Eaverage = 1
    hidout = np.zeros(hiddennum)
    y_delta = np.zeros(hiddennum)
    #M_iteration=[]
    #Eaverage_iteration = []
    while(M < iternum_max and Eaverage > Eaverage_min):
        Eall=0

        for i in range(trainnum):
            out=0
            for j in range(hiddennum):
                hidout[j]=sg(w_hide[j,0]*input_train[i,0]+w_hide[j,1]*input_train[i,1]-bias_hide[j])
                out += hidout[j] * w_out[j]
            out = sg(out - bias_out)
            E = abs(out_train[i] - out)
            Eall+=E      #损失函数
            delta = (out_train[i] - out) * out * (1 - out)
            for m in range(hiddennum):
                y_delta[m] = delta * w_out[m] * hidout[m] * (1 - hidout[m])
            bias_out -= step * delta
            for m in range(hiddennum):
                w_out[m] += step * delta * hidout[m]
                bias_hide[m] -= step * y_delta[m]
                w_hide[m,0]+=step * y_delta[m] * input_train[i,0]
                w_hide[m,1] += step * y_delta[m] * input_train[i,1]
        Eaverage=Eall/(trainnum)
        M += 1
        print("BP算法第",M,"次训练，归一化平均绝对误差为：",Eaverage)
        #M_iteration.append(M)
        #Eaverage_iteration.append(Eaverage)
    #平均绝对误差随迭代次数变化情况的散点图
    #M_iteration = np.array(M_iteration)
    #Eaverage_iteration = np.array(Eaverage_iteration)
    #plt.scatter(M_iteration,Eaverage_iteration,s=0.2)
    #plt.show()
    return w_hide,  bias_hide , w_out, bias_out

#测试单独使用bp算法的效果
if __name__ == "__main__":

    num = 1000  # 数据总数
    trainnum = int(0.9 * num)
    testnum = int(0.1 * num)  # 其中十分之一用测试

    # 用函数f(x)=2*x*x+sin(y+pi/4)生成数据集，其中自变量x，y的取值范围是(-2π，2π)
    input_data = np.random.uniform(low=-2 * pi, high=2 * pi, size=[num, 2])  # 第一列作为x，第二列作为y
    output_data = 2 * np.multiply(input_data[:, 0], input_data[:, 0]) + np.sin(input_data[:, 1] + pi / 4)

    # 归一化处理,将输入的范围调整到-1到1之间,输出范围调整到0到1之间
    output_max = np.max(output_data)
    output_min = np.min(output_data)
    input_datan = input_data / (2 * pi)
    output_datan = (output_data - output_min) / (output_max - output_min)

    # 9:1的比例划分训练集和测试集
    input_train = input_datan[0:int(0.9 * num), :]
    input_test = input_datan[int(0.9 * num):num, :]
    out_train = output_datan[0:int(0.9 * num)]
    out_test = output_datan[int(0.9 * num):num]
    out_testun = output_data[int(0.9 * num):num]   #未归一化的测试输出
    inputnum, outputnum = 2, 1  # 输入神经元，输出神经元个数

    #根据经验选择隐层节点数
    hiddennum = 20
    # 网络初始化
    w_hide = 2 * np.c_[np.random.random(hiddennum), np.random.random(hiddennum)] - 1  # 第i行j列表示第i个节点对第j个输入的权值
    bias_hide = 2 * np.random.random(hiddennum) - 1
    w_out = 2 * np.random.random(hiddennum) - 1
    bias_out = random.uniform(-1, 1)
    hidout = np.zeros(hiddennum)
    y_delta = np.zeros(hiddennum)
    # 得到训练后的神经网络
    w_hide, bias_hide, w_out, bias_out = BP(input_train, out_train, w_hide, bias_hide, w_out, bias_out, hiddennum, trainnum)

    # 计算测试集的误差
    E = 0
    outun = np.zeros(testnum)
    for i in range(testnum):
        out = 0
        for j in range(hiddennum):
            hidout[j] = sg(w_hide[j, 0] * input_test[i, 0] + w_hide[j, 1] * input_test[i, 1] - bias_hide[j])
            out += hidout[j] * w_out[j]
        out = sg(out - bias_out)
        outun[i]=(output_max - output_min) * out + output_min   #反归一化
        E += abs(out_test[i] - out)
    Etest_average = E / testnum
    print("\n用测试集测试")
    print("归一化平均绝对误差为：",Etest_average)

    # 作散点图
    plt.ion()
    ax = plt.axes(projection='3d')
    ax.scatter3D(2 * pi * input_test[:, 0], 2 * pi * input_test[:, 1], outun, 'binary')
    plt.title("The test result of BP"  + "\nTurn off automatically after 5 seconds")
    plt.pause(5)  # 显示5秒，5秒后自动关闭并继续运行
    plt.close()
    #print("\n画出拟合得到的函数图像，请稍候……")
    #plot_fittingimage(w_hide.transpose(), bias_hide, w_out.transpose(), bias_out,output_max,output_min,"BP")

4.2 泰坦尼克号源代码

这里要用到pytorch（实现方法和文章中的描述不完全相同，但是仍是值得一看的！），以及两个数据集atest.xls和atrain.xls。数据集是从官网上下载下来的，但是经过处理，excel截图如下。训练集共891条数据，测试集共418条数据。

GABP部分

#!/usr/bin/env python
#torch.__version__ = 1.2.0+cu92

"""
    GA.py
"""

from torch.autograd import Variable
from torch.nn import Parameter
from matplotlib import pyplot as plt
import torch
from torch import nn, optim
import torch.nn.functional as F
import pandas as pd
import random
import numpy as np

plt.rcParams['figure.figsize'] = (10, 10)

_ = np.random.seed(123)
_ = torch.manual_seed(123)

# 数据载入
file_path = r'E:\IAIRProjects\Python\Practice\homework\atrain.xls'

tr_pclass = pd.read_excel(file_path)['Pclass'].values
tr_sex = pd.read_excel(file_path)['Sex'].values
tr_age = pd.read_excel(file_path)['Age'].values
tr_sibsp = pd.read_excel(file_path)['SibSp'].values
tr_parch = pd.read_excel(file_path)['Parch'].values
tr_survive = pd.read_excel(file_path)['Survived'].values
# ts_pclass = pd.read_excel(file_path)['Pclass'].values
# ts_sex = pd.read_excel(file_path)['Sex'].values
# ts_age = pd.read_excel(file_path)['Age'].values
# ts_sibsp = pd.read_excel(file_path)['SibSp'].values
# ts_parch = pd.read_excel(file_path)['Parch'].values

file_path = r'E:\IAIRProjects\Python\Practice\homework\atest.xls'

ts_pclass = pd.read_excel(file_path)['Pclass'].values
ts_sex = pd.read_excel(file_path)['Sex'].values
ts_age = pd.read_excel(file_path)['Age'].values
ts_sibsp = pd.read_excel(file_path)['SibSp'].values
ts_parch = pd.read_excel(file_path)['Parch'].values


class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Conv1d(in_channels=5, out_channels=20, kernel_size=1, bias=True)
        self.conv2 = nn.Conv1d(in_channels=20, out_channels=20, kernel_size=1, bias=True)
        self.conv3 = nn.Conv1d(in_channels=20, out_channels=1, kernel_size=1, bias=True)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = self.conv3(x)
        return F.relu(x)


# Define GA worker
class Worker():

    def __init__(self, id, parameters):
        self.id = id
        self.acc = 0
        self.x = torch.stack((torch.from_numpy(tr_pclass).float(), torch.from_numpy(tr_sex).float(), torch.from_numpy(
            tr_age).float(), torch.from_numpy(tr_sibsp).float(), torch.from_numpy(tr_parch).float(), torch.from_numpy(
            tr_survive).float()), -1).t()

        # device = torch.device('cuda')
        # model = Lenet5()
        self.model = Model()
        if parameters == 0:
            pass
        else:
            self.model.load_weight(parameters)
        self.criteon = nn.MSELoss()
        self.optimizer = optim.Adam(self.model.parameters(), lr=0.002)

        print('Worker init ok')

    def train_model(self):
        for epoch in range(5):
            # print('epoch:', epoch)

            self.model.train()
            for i in range(890):
                # print(i)
                self.model.train()
                tmp = torch.randn(1, 5, 1)
                for j in range(4):
                    tmp[0][j] = self.x[j][i]
                logits = self.model(tmp)
                loss = self.criteon(logits, self.x[5][i])

                self.optimizer.zero_grad()
                loss.backward()
                self.optimizer.step()

            self.model.eval()
            with torch.no_grad():
                acc = 0
                for testi in range(890):
                    tmp = torch.randn(1, 5, 1)
                    for j in range(4):
                        tmp[0][j] = self.x[j][testi]
                    logits = self.model(tmp)
                    if logits <= 0.5:
                        ans = 0
                    else:
                        ans = 1
                    if ans == self.x[5][testi]:
                        acc = acc + 1

            print('epoch: ', self.id, '-', epoch, '-', acc)
            if acc > self.acc:
                self.acc = acc
            self.parameters = self.model.parameters

    def select(self, population):
        """ Copy theta from best member of the population """

        current_scores = [{
            "id": worker.id,
            "score": worker.acc,
        } for worker in population]

        best_worker = sorted(current_scores, key=lambda x: x['score'])[-1]

        if best_worker['id'] != self.id:
            self.model.parameters = population[best_worker['id']].parameters
        print('正确率：', population[best_worker['id']].acc/891)

    def mutation(self):
        """ Add normal noise to hyperparameter vector """
        with torch.no_grad():
            if random.random() > 0.8:
                tmp = Model()
                self.model.parameters = tmp.parameters


def run_experiment(do_mutation=False, do_select=False, n_steps=5):
    # Create population
    population = [
        Worker(id=0, parameters=0),
        Worker(id=1, parameters=0),
        Worker(id=2, parameters=0),
    ]

    print('Workers established')

    # Train
    for step in range(n_steps):

        print('step.:', step)

        for worker in population:
            worker.train_model()

            if do_select:
                # print('expoite')
                worker.select(population)

            if do_mutation:
                # print('mutation')
                worker.mutation()

    return population


def main():
    # Run experiments w/ various GA settings
    GA = run_experiment(do_mutation=True, do_select=True)  # mutation and select


if __name__ == '__main__':
    main()

BP部分，用来和GABP对比。

import torch
from torch import nn, optim
import torch.nn.functional as F
import numpy as np
import pandas as pd

# 数据载入
file_path = r'E:\IAIRProjects\Python\Practice\homework\atrain.xls'

tr_pclass = pd.read_excel(file_path)['Pclass'].values
tr_sex = pd.read_excel(file_path)['Sex'].values
tr_age = pd.read_excel(file_path)['Age'].values
tr_sibsp = pd.read_excel(file_path)['SibSp'].values
tr_parch = pd.read_excel(file_path)['Parch'].values
tr_survive = pd.read_excel(file_path)['Survived'].values
ts_pclass = pd.read_excel(file_path)['Pclass'].values
ts_sex = pd.read_excel(file_path)['Sex'].values
ts_age = pd.read_excel(file_path)['Age'].values
ts_sibsp = pd.read_excel(file_path)['SibSp'].values
ts_parch = pd.read_excel(file_path)['Parch'].values


class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Conv1d(in_channels=5, out_channels=20, kernel_size=1, bias=True)
        self.conv2 = nn.Conv1d(in_channels=20, out_channels=20, kernel_size=1, bias=True)
        self.conv3 = nn.Conv1d(in_channels=20, out_channels=1, kernel_size=1, bias=True)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = self.conv3(x)
        return F.relu(x)


def select(model):
    model.load_state_dict(torch.load('best.mdl'))
    print('model loaded!')
    model[3] = Model()
    criteon = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr=1e-3)

model = Model()
criteon = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)


# x = [tr_pclass, tr_sex, tr_age, tr_sibsp, tr_parch, tr_survive]

x = torch.stack((torch.from_numpy(tr_pclass).float(), torch.from_numpy(tr_sex).float(), torch.from_numpy(
    tr_age).float(), torch.from_numpy(tr_sibsp).float(), torch.from_numpy(tr_parch).float(), torch.from_numpy(
    tr_survive).float()), -1).t()

for epoch in range(10):
    print('epoch: ', epoch, '------------------------------------')
    for i in range(890):
        print(i)
        model.train()
        tmp = torch.randn(1, 5, 1)
        for j in range(4):
            tmp[0][j] = x[j][i]
        logits = model(tmp)
        loss = criteon(logits, x[5][i])
        # print(loss)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

torch.save(model.state_dict(), 'best.mdl')
acc = 0
for testi in range(890):
    tmp = torch.randn(1, 5, 1)
    for j in range(4):
        tmp[0][j] = x[j][testi]
    logits = model(tmp)
    if logits <= 0.5:
        print(0)
        ans = 0
    else:
        print(1)
        ans = 1
    print(x[5][testi])
    if ans == x[5][testi]:
        acc = acc + 1

print(acc / 891)

写了这么多内容，有没有人认真看呢？

如果有问题的话可以评论区留言，有错误的话欢迎指出。