线段树学习总结 - 关于猹 ACM 生涯的第一次受苦受难

title: 线段树学习总结 - 关于猹 ACM 生涯的第一次受苦受难
date: 2019-09-15

本文是关于线段树的 建树方法 和 建树原理 的讲解，如果你已经对于线段树的数据结构非常了解，请直接进入下一篇文章 线段树的基础操作

目录

• 线段树的意义
• 浅谈线段树（问题分析）
• 线段树的结构（数据结构）
  • 标记方法
  • 四倍原数据
• 线段树的小小总结
• 线段树的基础操作

线段树的意义

就像我在讨论搜索时一样，在讨论线段树之前我也想先思考一下线段树的实际意义。

随着逐渐深入对算法的学习和理解，会发现数据在计算机中的操作远比我们实际现实生活中能接触到的物体操作要复杂的多，大数据的意义也在我脑中逐渐清晰。当世界逐渐融合，各个领域逐渐贴近，新的对象产生新的数据、新的连接产生新的数据、新的融合产生新的数据、新的数据产生新的数据。。。错综复杂的数据是有如此多的分类，如此多的存在形式，如此多的 - 量。

只是在理解了世界上确实存在着那么大量的数据，由此才明白数据结构和算法存在的意义，当我第一次知道二叉搜索对时间的减少程度是如此之强时，我震惊了；当我知道快速排序强于冒泡排序的方式时，我感动了，算法太奇妙了【好像跑偏了】。就如同在数量级上万上亿的数据中搜索使用二叉搜索的道理一样，为了维护过于庞大的相关数据，线段树应运而生。

浅谈线段树（问题分析）

我们对于线段树最原始的理解不出意外都是：这里有一连串的数据，为了统计其中一段数据的和，或是对其中任意一段数据的每个单独数据都进行某种操作。若是每次都将这些数据依次更新，然后再依次求和，那么对于过于大量的数据来说，未免太过缓慢。就像前文说的一样，往广阔的世界去思考，处理数据的人（或机器）的时间是有限的，而制造数据的人（或机器）却是成千上万同时进行的，因此为了提到我们处理数据的效率，必须要想出一种方式去加快（求和或处理）操作的速度，至少努力去试一下。

既然是对一段连续的数据进行操作的，那么我们可以想一种方法将这一段数据变成一个数据，如果考虑到实际的线段树我们也可以说是将很多数据变成尽量少个数据，用少量的数据来表示原本大量的数据，之后再逐个操作（嗯？仿佛回到了原点）。至少我们减少了要处理的数据的量，用这种思路来提高效率。

线段树的结构（数据结构）

最简单的处理数据的容器就是数组，而数组是线性储存的容器，如何构建一个树形储存呢？别着急，我们先知道使用的是数组，然后先来看一下线段树的样子：

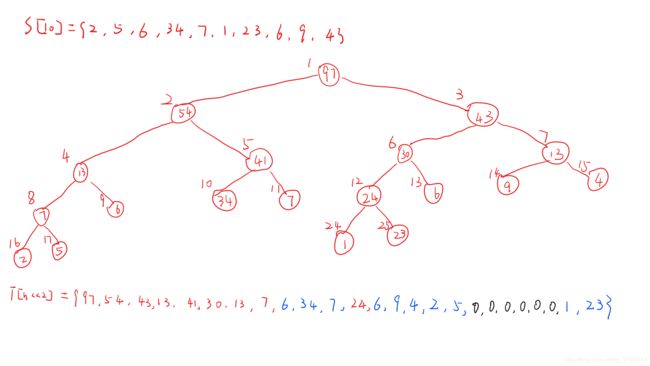
举个栗子，假设我们要处理的数据是 S[10] = {2, 5, 6, 34, 7, 1, 23, 6, 9, 4} ，记住它的顺序，然后来看看树怎么画

通过这个简单的求和树可以看到：

1. 线段树的造型是一个二叉树；
2. 原数据都在最底端不再分叉的节点上，即叶子节点；
3. 除了叶子节点，每个节点的值都是它所分叉出来的两个节点的和；
4. 树的层数取决于我们需要的叶子节点的个数（即原数据的个数），层数为 $$lo{g}_2^n$$ 向上取整后加 1 。

比如我们现在有 10 个数，那么线段树的层数就是 5 。事实上我们并不需要知道线段树的层数，也不需要知道节点个数，因为实际上程序操作时都是通过递归进行的，我们这一步的主要任务记住这个图的样子，接下来我们来讨论如何用 数组 来存 树。

现在大家可以自己尝试给这个树的节点标上每个点在数组中的位置，由于这里是博文所以就没法不卖关子了

我们会发现，这个标法还挺好理解的哈。这里我还在下面写出了储存树的数组 T 中的元素，我们会发现， 红色 的是自动生成的节点的数， 蓝色 是叶子节点的数， 黑色 的 0 是没有用到但是必须开辟的一些空间。因此引出接下来的话题：

这样标虽然好看，可是程序是怎么处理的呢，接下来我要强调的两个点是我看过了不算很多的线段树讲解的博客和视频中都没有提到的两个重点。

标记方法

这一点总归刚刚已经跟你们说过了，树的数据在数组里就是这样存储的，虽然各种算法讲解都会跟你们写出来 t << 1, t << 1|1 这样的代码，可是就是不跟你解释为什么要这样写。

可以看到原数据所在的位置，实际上就是 树 的最底层，而树的最层数是由原数的个数决定的，原因我们直接看代码

#include 

//假设原始数据最多有 1000 个
#define MAXN int(1e3 + 9)
//线段树操作的通用形参
#define DEFI int l, int r, int t
//主函数中使用的初始值
#define INIF 1, n, 1
//递归时使用的 左子节点 和 右子节点
#define LSON l, (l + r) >> 1, t << 1
#define RSON ((l + r) >> 1) + 1, r, t << 1|1

using namespace std;

//S - 原始数据，T - 树
int S[MAXN], T[MAXN << 2];

void build(DEFI) {
	if (l == r) {
		T[t] = S[l];
		return ;
	}
	build(LSON);
	build(RSON);
	T[t] = T[t << 1] + T[t << 1|1];
	return ;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> S[i];
	build(INIF);
	return 0;
}

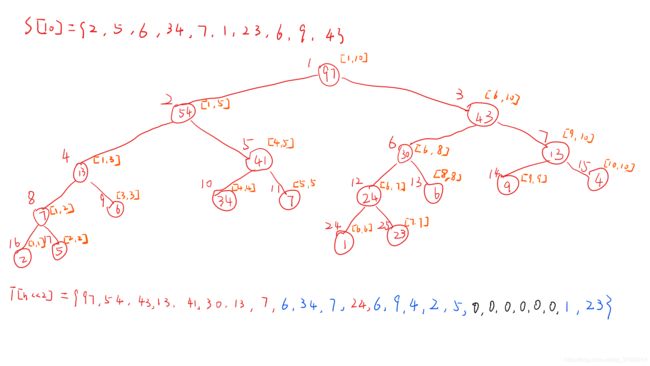
可以看到树的节点在数组中的位置是变量 t ，而这个 t 每次进入下一层时向左扩展的方式是 乘以二 向右扩展的方式是 乘二加一 ，由此生成了一个节点的两个子节点，而这个节点所管理的 范围 又是什么呢，就是函数形参中的 l 和 r 。

现在我们标上范围

可以看到节点表示的范围已经标出来了，中括号中的两个数实际上就是 l 和 r 的值。因此当 l == r 时，实际上就已经到了叶子节点，而且节点的 l 的值与原数据的位置（存在于 S 中的下标）恰好是一致的。我发现这一点的时候真的很惊讶，所以确实是 “恰好” ，这是个巧合还是一个阴谋。

总之如何这样建树的原因到此已经解释清楚了，每一个节点都通过 << 1 和 << 1|1 来得到子节点的位置，这种递归的方式能够完美的根据原数据的量来找到不会冲突的空间，从而使每一个节点都能有地方去。下面我们解释一个小细节。

四倍原数据

我一开始理解线段树了以后第一次尝试写代码做模板题，然后就总是 运行错误 ，寻找最美越界数组最后对照大佬代码两天才明白原来人家 << 2 了一下，但是题解没有解释这样做的原因。百度线段树开四倍数组，最后知道了原理。

观察样图不难发现，原数据都存在最末端的叶子节点，然而有事我们为了获得足够的叶子节点会在 “看起来很多节点” 的一层的下一层多产生一层，就为了添加那么一两个节点。但是如果数据在达到 " 2 的整次幂" 之后再添加一个数据，树就必须多添加一层，那么这一部分空间是必须预留的。例如我们的 10 个数据，8 个数据刚好填满第四层的节点，添加一个还好，是在节点 “8” 添加两个子节点，与第四层最后的 “15” 刚好接轨访问 “16” 和 “17” ，但是如果再加一个数据，由于我们用 l == r 来表示第 l （或 r ，这无所谓，因为叶子节点 l = r ）个数存储的位置，而树中的节点位置是用 “t” 来控制的，l = r = 6 的时候 t 是在 l = r = 5 的下一个相邻的节点，所以理所当然在 l = r = 5 的下一个 已经存在的 相邻的节点来扩充树，因此一下从离 15 很近的 17 拓展到 “离得过远” 的 25 。

接下来我们看一下列表展示

原数据个数	层数	节点数	需要数组数	实际开辟空间
4	3	7	7	7
8	4	15	15	15
9	5	17	17	31
10	5	19	25	31

树的层数	底层节点数	除底层外的节点数
2	2	1
3	4	3
4	8	7
5	16	15

通过以上两个表不难发现 - 节点数 大约是 原数据个数 的 两倍 ，而如果要新开辟一层，会发现 最后一层 又是上面的所有节点的个数加一，因此我们可以简单的从此看出需要 “原数据四倍的空间” 。

_{网上有证明过程，在意的自行百度。}

---

至此，整个线段树的第一部分完成了。

线段树的小小总结

1. 意义：能够快速对大量数据中的一段连续数据进行简单处理（事实上是只支持 符合结合律 的算术），简单迅速的对一段连续数据进行读取；
2. 构建：节点对应的左右边界就是管理的区间范围，树储存在数组的方式是从树顶开始从左到右依次标号，左节点标号为父节点标号的两倍，右节点标号为父节点标号的两倍加一；
3. 注意：最后一层的扩点方式，存树的数组开原数据量的四倍。

由于线段树一开始的理解太过复杂，对于我来说，线段树的数据结构的构建，尤其是怎么把 “树” 存到 “数组” 里，暑假的时候我是照着模板题的样例一点一点记录，一点一点分析成勋运行过程中变量的变化才慢慢发现了规律，明白了原理。

因此我不惜用一整篇文章来单独讨论线段树的数据结构的构建，只是为了让大家（以及未来忘记了的猹）能够充分的理解线段树的构建原理。只要理解了线段树是怎么建树的，想要拓展想必就会轻松很多（虽然并不轻松），起码这是学习线段树的基础。

接下来的线段树请观看 线段树的基础操作

参考文章：[洛谷日报第4期]浅谈线段树——Segment Tree

请多多支持猹的个人博客，这里的文章那里也都有 H_On 个人小站
因为猹的小站真的还挺可的，所以那边更新的也比较勤奋，感谢关注~我会努力的(ง •_•)ง