NNDL 实验六 卷积神经网络（3）LeNet实现MNIST

5.3 基于LeNet实现手写体数字识别实验 

5.3.1 数据 

手写体数字识别是计算机视觉中最常用的图像分类任务，让计算机识别出给定图片中的手写体数字（0-9共10个数字）。由于手写体风格差异很大，因此手写体数字识别是具有一定难度的任务。

我们采用常用的手写数字识别数据集：MNIST数据集。

MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges

MNIST数据集是计算机视觉领域的经典入门数据集，包含了60,000个训练样本和10,000个测试样本。

这些数字已经过尺寸标准化并位于图像中心，图像是固定大小(28×28像素)。

LeNet-5虽然提出的时间比较早，但它是一个非常成功的神经网络模型。

基于LeNet-5的手写数字识别系统在20世纪90年代被美国很多银行使用，用来识别支票上面的手写数字。

 为了节省训练时间，本节选取MNIST数据集的一个子集进行后续实验，数据集的划分为：

• 训练集：1,000条样本
• 验证集：200条样本
• 测试集：200条样本

MNIST数据集分为train_set、dev_set和test_set三个数据集，每个数据集含两个列表分别存放了图片数据以及标签数据。比如train_set包含：

• 图片数据：[1 000, 784]的二维列表，包含1 000张图片。每张图片用一个长度为784的向量表示，内容是 28×2828×28 尺寸的像素灰度值（黑白图片）。
• 标签数据：[1 000, 1]的列表，表示这些图片对应的分类标签，即0~9之间的数字。

观察数据集分布情况，代码实现如下：

import os
import struct
import numpy as np

# 读取标签数据集
with open('./train-labels.idx1-ubyte', 'rb') as lbpath:
    labels_magic, labels_num = struct.unpack('>II', lbpath.read(8))
    labels = np.fromfile(lbpath, dtype=np.uint8)

# 读取图片数据集
with open('./train-images.idx3-ubyte', 'rb') as imgpath:
    images_magic, images_num, rows, cols = struct.unpack('>IIII', imgpath.read(16))
    images = np.fromfile(imgpath, dtype=np.uint8).reshape(images_num, rows * cols)

train_images, train_labels = images[:1000], labels[:1000]
dev_images, dev_labels = images[1000:1200], labels[1000:1200]
test_images, test_labels = images[1200:1400], labels[1200:1400]
train_set, dev_set, test_set = [train_images, train_labels], [dev_images, dev_labels], [test_images, test_labels]
print('Length of train/dev/test set:{}/{}/{}'.format(len(train_set[0]), len(dev_set[0]), len(test_set[0])))

Length of train/dev/test set:1000/200/200

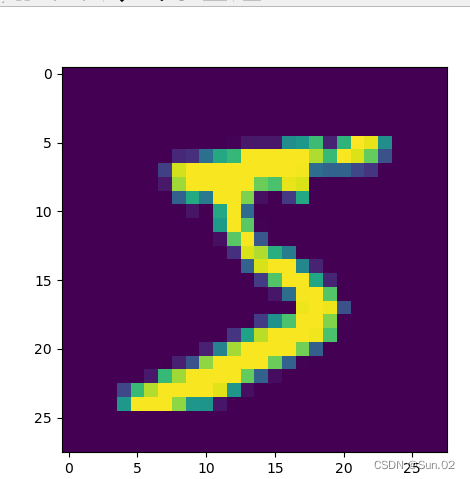
 可视化观察其中的一张样本以及对应的标签，代码如下所示： 

import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
 
image, label = train_set[0][0], train_set[1][0]
image, label = np.array(image).astype('float32'), int(label)
# 原始图像数据为长度784的行向量，需要调整为[28,28]大小的图像
image = np.reshape(image, [28,28])
image = Image.fromarray(image.astype('uint8'), mode='L')
print("The number in the picture is {}".format(label))
plt.figure(figsize=(5, 5))
plt.imshow(image)
plt.savefig('conv-number5.pdf')

The number in the picture is 5

5.3.1.1 数据预处理 

图像分类网络对输入图片的格式、大小有一定的要求，数据输入模型前，需要对数据进行预处理操作，使图片满足网络训练以及预测的需要。本实验主要应用了如下方法：

调整图片大小：LeNet网络对输入图片大小的要求为 32×3232×32 ，而MNIST数据集中的原始图片大小却是 28×2828×28 ，这里为了符合网络的结构设计，将其调整为32×3232×32；
规范化： 通过规范化手段，把输入图像的分布改变成均值为0，标准差为1的标准正态分布，使得最优解的寻优过程明显会变得平缓，训练过程更容易收敛。

import torchvision.transforms as transforms
 
# 数据预处理
transforms = transforms.Compose([transforms.Resize(32),transforms.ToTensor(), transforms.Normalize(mean=[0.5], std=[0.5])])

将原始的数据集封装为Dataset类，以便DataLoader调用。 

import random
from torch.utils.data import Dataset,DataLoader
 
class MNIST_dataset(Dataset):
    def __init__(self, dataset, transforms, mode='train'):
        self.mode = mode
        self.transforms =transforms
        self.dataset = dataset
 
    def __getitem__(self, idx):
        # 获取图像和标签
        image, label = self.dataset[0][idx], self.dataset[1][idx]
        image, label = np.array(image).astype('float32'), int(label)
        image = np.reshape(image, [28,28])
        image = Image.fromarray(image.astype('uint8'), mode='L')
        image = self.transforms(image)
 
        return image, label
 
    def __len__(self):
        return len(self.dataset[0])
 
 
# 加载 mnist 数据集
train_dataset = MNIST_dataset(dataset=train_set, transforms=transforms, mode='train')
test_dataset = MNIST_dataset(dataset=test_set, transforms=transforms, mode='test')
dev_dataset = MNIST_dataset(dataset=dev_set, transforms=transforms, mode='dev')

5.3.2 模型构建

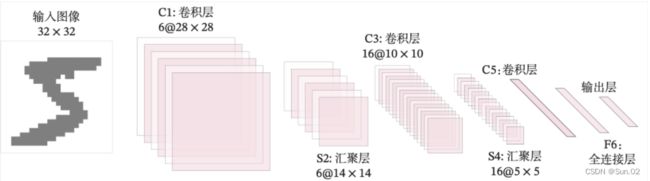
LeNet-5虽然提出的时间比较早，但它是一个非常成功的神经网络模型。基于LeNet-5的手写数字识别系统在20世纪90年代被美国很多银行使用，用来识别支票上面的手写数字。LeNet-5的网络结构如下图所示。

我们使用上面定义的卷积层算子和汇聚层算子构建一个LeNet-5模型。

这里的LeNet-5和原始版本有4点不同：

1.C3层没有使用连接表来减少卷积数量。
2.汇聚层使用了简单的平均汇聚，没有引入权重和偏置参数以及非线性激活函数。
3.卷积层的激活函数使用ReLU函数。
4.最后的输出层为一个全连接线性层。
网络共有7层，包含3个卷积层、2个汇聚层以及2个全连接层的简单卷积神经网络接，受输入图像大小为32×32=1024，输出对应10个类别的得分。

import torch.nn.functional as F
import torch.nn as nn
 
class Model_LeNet(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Model_LeNet, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5×5
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2×2，步长为2
        self.pool2 = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5×5，步长为1
        self.conv3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1)
        # 汇聚层：汇聚窗口为2×2，步长为2
        self.pool4 = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5×5
        self.conv5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5, stride=1)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(120, 84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(84, num_classes)
 
    def forward(self, x):
        # C1：卷积层+激活函数
 
        output = F.relu(self.conv1(x))
        # S2：汇聚层
        output = self.pool2(output)
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return output

 下面测试一下上面的LeNet-5模型，构造一个形状为 [1,1,32,32]的输入数据送入网络，观察每一层特征图的形状变化。代码实现如下： 

# 这里用np.random创建一个随机数组作为输入数据
inputs = np.random.randn(*[1, 1, 32, 32])
inputs = inputs.astype('float32')
# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
print(model)
# 通过调用LeNet从基类继承的sublayers()函数，查看LeNet中所包含的子层
print(model.named_parameters())
x = torch.tensor(inputs)
print(x)
for item in model.children():
    # item是LeNet类中的一个子层
    # 查看经过子层之后的输出数据形状
    item_shapex = 0
    names = []
    parameter = []
    for name in item.named_parameters():
        names.append(name[0])
        parameter.append(name[1])
        item_shapex += 1
    try:
        x = item(x)
    except:
        # 如果是最后一个卷积层输出，需要展平后才可以送入全连接层
        x = x.reshape([x.shape[0], -1])
        x = item(x)
 
    if item_shapex == 2:
        # 查看卷积和全连接层的数据和参数的形状，
        # 其中item.parameters()[0]是权重参数w，item.parameters()[1]是偏置参数b
        print(item, x.shape, parameter[0].shape, parameter[1].shape)
    else:
        # 汇聚层没有参数
        print(item, x.shape)

输出 

Model_LeNet(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (pool2): MaxPool2d(kernel_size=(2, 2), stride=2, padding=0, dilation=1, ceil_mode=False)
  (conv3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (pool4): AvgPool2d(kernel_size=(2, 2), stride=2, padding=0)
  (conv5): Conv2d(16, 120, kernel_size=(5, 5), stride=(1, 1))
  (linear6): Linear(in_features=120, out_features=84, bias=True)
  (linear7): Linear(in_features=84, out_features=10, bias=True)
)

tensor([[[[-0.6168, -1.6454,  0.5935,  ...,  0.6808,  0.0304,  1.7876],
          [ 0.8079, -1.0423,  0.0298,  ..., -0.3931, -2.0819,  0.1984],
          [-1.9750, -0.1246,  0.5665,  ..., -0.6475, -1.8675, -0.5194],
          ...,
          [ 0.1182, -0.7900, -0.0170,  ...,  0.6823,  1.0729,  0.2501],
          [-0.5092,  0.7907,  0.2355,  ..., -0.0219, -1.5584, -0.9035],
          [ 1.7203, -0.8788,  0.3646,  ...,  0.6160,  2.0292, -1.5413]]]])
Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1)) torch.Size([1, 6, 28, 28]) torch.Size([6, 1, 5, 5]) torch.Size([6])
MaxPool2d(kernel_size=(2, 2), stride=2, padding=0, dilation=1, ceil_mode=False) torch.Size([1, 6, 14, 14])
Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1)) torch.Size([1, 16, 10, 10]) torch.Size([16, 6, 5, 5]) torch.Size([16])
AvgPool2d(kernel_size=(2, 2), stride=2, padding=0) torch.Size([1, 16, 5, 5])
Conv2d(16, 120, kernel_size=(5, 5), stride=(1, 1)) torch.Size([1, 120, 1, 1]) torch.Size([120, 16, 5, 5]) torch.Size([120])
Linear(in_features=120, out_features=84, bias=True) torch.Size([1, 84]) torch.Size([84, 120]) torch.Size([84])
Linear(in_features=84, out_features=10, bias=True) torch.Size([1, 10]) torch.Size([10, 84]) torch.Size([10])

从输出结果看，

对于大小为32×32的单通道图像，先用6个大小为5×5的卷积核对其进行卷积运算，输出为6个28×28大小的特征图；
6个28×28大小的特征图经过大小为2×2，步长为2的汇聚层后，输出特征图的大小变为14×1414×14；
6个14×14大小的特征图再经过16个大小为5×5的卷积核对其进行卷积运算，得到16个10×10大小的输出特征图；
16个10×10大小的特征图经过大小为2×2，步长为2的汇聚层后，输出特征图的大小变为5×5；
16个5×5大小的特征图再经过120个大小为5×5的卷积核对其进行卷积运算，得到120个1×1大小的输出特征图；
此时，将特征图展平成1维，则有120个像素点，经过输入神经元个数为120，输出神经元个数为84的全连接层后，输出的长度变为84。
再经过一个全连接层的计算，最终得到了长度为类别数的输出结果。

考虑到自定义的Conv2D和Pool2D算子中包含多个for循环，所以运算速度比较慢。pytorch中，针对卷积层算子和汇聚层算子进行了速度上的优化，这里基于torch.nn.Conv2d()；torch.nn.MaxPool2d()；torch.nn.avg_pool2d()构建LeNet-5模型，对比与上边实现的模型的运算速度。代码实现如下：

class Torch_LeNet(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Torch_LeNet, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5*5
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5*5
        self.conv3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool4 = nn.AvgPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5*5
        self.conv5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(in_features=120, out_features=84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(in_features=84, out_features=num_classes)
 
    def forward(self, x):
        # C1：卷积层+激活函数
        output = F.relu(self.conv1(x))
        # S2：汇聚层
        output = self.pool2(output)
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return output

测试两个网络的运算速度。 

import time
 
# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[1,1,32,32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)
 
# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
# 创建Torch_LeNet类的实例，指定模型名称和分类的类别数目
torch_model = Torch_LeNet(in_channels=1, num_classes=10)
 
# 计算Model_LeNet类的运算速度
model_time = 0
for i in range(60):
    strat_time = time.time()
    out = model(x)
    end_time = time.time()
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    model_time += (end_time - strat_time)
avg_model_time = model_time / 50
print('Model_LeNet speed:', avg_model_time, 's')
# 计算Torch_LeNet类的运算速度
torch_model_time = 0
for i in range(60):
    strat_time = time.time()
    torch_out = torch_model(x)
    end_time = time.time()
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    torch_model_time += (end_time - strat_time)
avg_torch_model_time = torch_model_time / 50
 
print('Torch_LeNet speed:', avg_torch_model_time, 's')

输出

Model_LeNet speed: 0.0008378362655639648 s
Torch_LeNet speed: 0.000997304916381836 s

可以看到，输出结果是一致的。

这里还可以统计一下LeNet-5模型的参数量和计算量。

参数量

按照公式(5.18)进行计算，可以得到：

第一个卷积层的参数量为：6×1×5×5+6=1566×1×5×5+6=156；
第二个卷积层的参数量为：16×6×5×5+16=241616×6×5×5+16=2416；
第三个卷积层的参数量为：120×16×5×5+120=48120120×16×5×5+120=48120；
第一个全连接层的参数量为：120×84+84=10164120×84+84=10164；
第二个全连接层的参数量为：84×10+10=85084×10+10=850；
所以，LeNet-5总的参数量为6170661706。

在pytorch中，还可以使用torchsummaryAPI自动计算参数量。

from torchsummary import summary
model = Torch_LeNet(in_channels=1, num_classes=10)
params_info = summary(model, (1, 32, 32))
print(params_info)

输出

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1            [-1, 6, 28, 28]             156
         MaxPool2d-2            [-1, 6, 14, 14]               0
            Conv2d-3           [-1, 16, 10, 10]           2,416
         AvgPool2d-4             [-1, 16, 5, 5]               0
            Conv2d-5            [-1, 120, 1, 1]          48,120
            Linear-6                   [-1, 84]          10,164
            Linear-7                   [-1, 10]             850
================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.06
Params size (MB): 0.24
Estimated Total Size (MB): 0.30
----------------------------------------------------------------
None

可以看到，结果与公推导一致。

计算量

按照公式(5.19)进行计算，可以得到：

第一个卷积层的计算量为：28×28×5×5×6×1+28×28×6=122304；
第二个卷积层的计算量为：10×10×5×5×16×6+10×10×16=241600；
第三个卷积层的计算量为：1×1×5×5×120×16+1×1×120=48120；
平均汇聚层的计算量为：16×5×5=400；
第一个全连接层的计算量为：120×84=10080；
第二个全连接层的计算量为：84×10=840；
所以，LeNet-5总的计算量为423344。

5.3.3 模型训练 

使用交叉熵损失函数，并用随机梯度下降法作为优化器来训练LeNet-5网络。
用RunnerV3在训练集上训练5个epoch，并保存准确率最高的模型作为最佳模型。 

import torch.optim as opti
torch.manual_seed(100)
# 学习率大小
lr = 0.1
# 批次大小
batch_size = 64
# 加载数据
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = DataLoader(dev_dataset, batch_size=batch_size)
test_loader = DataLoader(test_dataset, batch_size=batch_size)
model = Model_LeNet(in_channels=1, num_classes=10)
optimizer = opti.SGD(model.parameters(), 0.2)
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
metric = Accuracy()
# 实例化 RunnerV3 类，并传入训练配置。
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader, num_epochs=6, log_steps=log_steps,
                eval_steps=eval_steps, save_path="best_model.pdparams")
 

输出

[Train] epoch: 0/6, step: 0/282, loss: 2.29467
[Train] epoch: 0/6, step: 15/282, loss: 2.28796
[Evaluate]  dev score: 0.11000, dev loss: 2.29656
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.11000
[Train] epoch: 0/6, step: 30/282, loss: 2.23975
[Evaluate]  dev score: 0.28000, dev loss: 2.24914
[Evaluate] best accuracy performence has been updated: 0.11000 --> 0.28000
[Train] epoch: 0/6, step: 45/282, loss: 2.14549
[Evaluate]  dev score: 0.14000, dev loss: 2.21046
[Train] epoch: 1/6, step: 60/282, loss: 1.53033
[Evaluate]  dev score: 0.28000, dev loss: 2.03015
[Train] epoch: 1/6, step: 75/282, loss: 1.76938
[Evaluate]  dev score: 0.43500, dev loss: 1.50521
[Evaluate] best accuracy performence has been updated: 0.28000 --> 0.43500
[Train] epoch: 1/6, step: 90/282, loss: 0.74312
[Evaluate]  dev score: 0.72000, dev loss: 0.88398
[Evaluate] best accuracy performence has been updated: 0.43500 --> 0.72000
[Train] epoch: 2/6, step: 105/282, loss: 0.54866
[Evaluate]  dev score: 0.82500, dev loss: 0.46658
[Evaluate] best accuracy performence has been updated: 0.72000 --> 0.82500
[Train] epoch: 2/6, step: 120/282, loss: 0.32134
[Evaluate]  dev score: 0.79500, dev loss: 0.54553
[Train] epoch: 2/6, step: 135/282, loss: 0.38424
[Evaluate]  dev score: 0.90000, dev loss: 0.28482
[Evaluate] best accuracy performence has been updated: 0.82500 --> 0.90000
[Train] epoch: 3/6, step: 150/282, loss: 0.08964
[Evaluate]  dev score: 0.89000, dev loss: 0.29195
[Train] epoch: 3/6, step: 165/282, loss: 0.42120
[Evaluate]  dev score: 0.84000, dev loss: 0.43841
[Train] epoch: 3/6, step: 180/282, loss: 0.46647
[Evaluate]  dev score: 0.87500, dev loss: 0.32823
[Train] epoch: 4/6, step: 195/282, loss: 0.28612
[Evaluate]  dev score: 0.88000, dev loss: 0.33385
[Train] epoch: 4/6, step: 210/282, loss: 0.15028
[Evaluate]  dev score: 0.95000, dev loss: 0.17772
[Evaluate] best accuracy performence has been updated: 0.90000 --> 0.95000
[Train] epoch: 4/6, step: 225/282, loss: 0.11253
[Evaluate]  dev score: 0.95000, dev loss: 0.13939
[Train] epoch: 5/6, step: 240/282, loss: 0.08045
[Evaluate]  dev score: 0.93000, dev loss: 0.24721
[Train] epoch: 5/6, step: 255/282, loss: 0.13160
[Evaluate]  dev score: 0.90000, dev loss: 0.28647
[Train] epoch: 5/6, step: 270/282, loss: 0.22351
[Evaluate]  dev score: 0.95500, dev loss: 0.13278
[Evaluate] best accuracy performence has been updated: 0.95000 --> 0.95500
[Evaluate]  dev score: 0.94500, dev loss: 0.13454
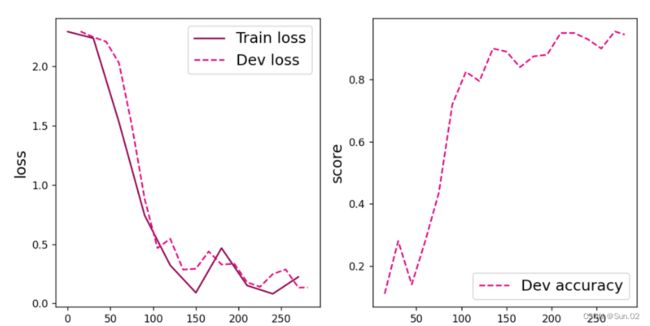
[Train] Training done!

可视化观察训练集与验证集的损失变化情况 

# 可视化误差
def plot(runner, fig_name):
    plt.figure(figsize=(10, 5))
 
    plt.subplot(1, 2, 1)
    train_items = runner.train_step_losses[::30]
    train_steps = [x[0] for x in train_items]
    train_losses = [x[1] for x in train_items]
 
    plt.plot(train_steps, train_losses, color='#8E004D', label="Train loss")
    if runner.dev_losses[0][0] != -1:
        dev_steps = [x[0] for x in runner.dev_losses]
        dev_losses = [x[1] for x in runner.dev_losses]
        plt.plot(dev_steps, dev_losses, color='#E20079', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='x-large')
    plt.xlabel("step", fontsize='x-large')
    plt.legend(loc='upper right', fontsize='x-large')
 
    plt.subplot(1, 2, 2)
    # 绘制评价准确率变化曲线
    if runner.dev_losses[0][0] != -1:
        plt.plot(dev_steps, runner.dev_scores,
                 color='#E20079', linestyle="--", label="Dev accuracy")
    else:
        plt.plot(list(range(len(runner.dev_scores))), runner.dev_scores,
                 color='#E20079', linestyle="--", label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='x-large')
    plt.xlabel("step", fontsize='x-large')
    plt.legend(loc='lower right', fontsize='x-large')
 
    plt.savefig(fig_name)
    plt.show()
 
 
runner.load_model('best_model.pdparams')
plot(runner, 'cnn-loss1.pdf')

5.3.4 模型评价 

使用测试数据对在训练过程中保存的最佳模型进行评价，观察模型在测试集上的准确率以及损失变化情况。

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))

输出

[Test] accuracy/loss: 0.8620/0.4243

5.3.5 模型预测 

同样地，我们也可以使用保存好的模型，对测试集中的某一个数据进行模型预测，观察模型效果。

# 获取测试集中第一条数
X, label = next(iter(test_loader))
logits = runner.predict(X)
# 多分类，使用softmax计算预测概率
pred = F.softmax(logits,dim=1)
print(pred.shape)
# 获取概率最大的类别
pred_class = torch.argmax(pred[2]).numpy()
print(pred_class)
label = label[2].numpy()
# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))
# 可视化图片
plt.figure(figsize=(2, 2))
image, label = test_set[0][2], test_set[1][2]
image= np.array(image).astype('float32')
image = np.reshape(image, [28,28])
image = Image.fromarray(image.astype('uint8'), mode='L')
plt.imshow(image)
plt.savefig('cnn-number2.pdf')

输出

torch.Size([64, 10])
1
The true category is 1 and the predicted category is 1

使用前馈神经网络实现MNIST识别，与LeNet效果对比。（选做） 

import struct
import numpy as np
import torch.optim as opt
from nndl import runnerV3, metric
import random
import torch.utils.data as io
import torch.nn.functional as F
import torch.nn as nn
import torch
from PIL import Image
import matplotlib.pyplot as plt
from torchvision.transforms import Compose, Resize, Normalize
import torchvision.transforms as transforms
import torchmetrics
from nndl.dataset import load_data
class Accuracy(torchmetrics.Metric):
    def __init__(self,is_logist=True):
        """
        输入：
           - is_logist: outputs是logist还是激活后的值
        """
        # 用于统计正确的样本个数
        super().__init__()
        self.add_state("num_correct",torch.tensor(0))
        # 用于统计样本的总数
        self.add_state("num_count", torch.tensor(0))
        #self.add_state("is_logist", is_logist)
    def update(self, outputs, labels):
        """
        输入：
           - outputs: 预测值, shape=[N,class_num]
           - labels: 标签值, shape=[N,1]
        """
 
        # 判断是二分类任务还是多分类任务，shape[1]=1时为二分类任务，shape[1]>1时为多分类任务
        if outputs.shape[1] == 1: # 二分类
            outputs = torch.squeeze(outputs, -1)
            if self.is_logist:
                # logist判断是否大于0
                p = []
                for i in range(len(outputs)):
                    if outputs[i] > 0.:
                        p.append([1])
                    else:
                        p.append([0])
                preds = torch.tensor(p)
            else:
                # 如果不是logist，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
                p = []
                for i in range(len(outputs)):
                    if outputs[i] > 0.5:
                        p.append([1])
                    else:
                        p.append([0])
                preds = torch.tensor(p)
        else:
            # 多分类时，使用'paddle.argmax'计算最大元素索引作为类别
            preds = torch.argmax(outputs, dim=1).int()
 
        # 获取本批数据中预测正确的样本个数
        labels = torch.squeeze(labels, -1)
        batch_correct = torch.sum(torch.eq(preds, labels).float()).numpy()
        batch_count = len(labels)
 
        # 更新num_correct 和 num_count
        self.num_correct += batch_correct
        self.num_count += batch_count
 
    def compute(self):
        # 使用累计的数据，计算总的指标
        if self.num_count == 0:
            return 0
        return self.num_correct / self.num_count
 
    def reset(self):
        # 重置正确的数目和总数
        self.num_correct = 0
        self.num_count = 0
 
    def name(self):
        return "Accuracy"
class Model_MLP_L2_V3(nn.Module):
    def __init__(self, input_size, output_size, hidden_size):
        super(Model_MLP_L2_V3, self).__init__()
        # 构建第一个全连接层
        self.fc1 = nn.Linear(
            input_size,
            hidden_size,
        )
        nn.init.normal_(self.fc1.weight, mean=0, std=0.01)
        nn.init.constant_(self.fc1.bias,1.0)
        # 构建第二全连接层
        self.fc2 = nn.Linear(
            hidden_size,
            output_size,
        )
        nn.init.normal_(self.fc2.weight, mean=0, std=0.01)
        nn.init.constant_(self.fc2.bias, 1.0)
        # 定义网络使用的激活函数
        self.act = nn.Sigmoid()
 
    def forward(self, inputs):
        outputs = self.fc1(inputs)
        outputs = self.act(outputs)
        outputs = self.fc2(outputs)
        return outputs
class RunnerV3(object):
    def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric  # 只用于计算评价指标
 
        # 记录训练过程中的评价指标变化情况
        self.dev_scores = []
 
        # 记录训练过程中的损失函数变化情况
        self.train_epoch_losses = []  # 一个epoch记录一次loss
        self.train_step_losses = []  # 一个step记录一次loss
        self.dev_losses = []
 
        # 记录全局最优指标
        self.best_score = 0
 
    def train(self, train_loader, dev_loader=None, **kwargs):
        # 将模型切换为训练模式
        self.model.train()
 
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_steps = kwargs.get("log_steps", 100)
        # 评价频率
        eval_steps = kwargs.get("eval_steps", 0)
 
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")
 
        custom_print_log = kwargs.get("custom_print_log", None)
 
        # 训练总的步数
        num_training_steps = num_epochs * len(train_loader)
 
        if eval_steps:
            if self.metric is None:
                raise RuntimeError('Error: Metric can not be None!')
            if dev_loader is None:
                raise RuntimeError('Error: dev_loader can not be None!')
 
        # 运行的step数目
        global_step = 0
 
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            # 用于统计训练集的损失
            total_loss = 0
            for step, data in enumerate(train_loader):
                X, y = data
                # 获取模型预测
                logits = self.model(X)
                loss = self.loss_fn(logits, y)  # 默认求mean
                total_loss += loss
 
                # 训练过程中，每个step的loss进行保存
                self.train_step_losses.append((global_step, loss.item()))
 
                if log_steps and global_step % log_steps == 0:
                    print(
                        f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")
 
                # 梯度反向传播，计算每个参数的梯度值
                loss.backward()
 
                if custom_print_log:
                    custom_print_log(self)
 
                # 小批量梯度下降进行参数更新
                self.optimizer.step()
                # 梯度归零
                optimizer.zero_grad()
 
                # 判断是否需要评价
                if eval_steps > 0 and global_step > 0 and \
                        (global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):
 
                    dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
                    print(f"[Evaluate]  dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")
 
                    # 将模型切换为训练模式
                    self.model.train()
 
                    # 如果当前指标为最优指标，保存该模型
                    if dev_score > self.best_score:
                        self.save_model(save_path)
                        print(
                            f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
                        self.best_score = dev_score
 
                global_step += 1
 
            # 当前epoch 训练loss累计值
            trn_loss = (total_loss / len(train_loader)).item()
            # epoch粒度的训练loss保存
            self.train_epoch_losses.append(trn_loss)
 
        print("[Train] Training done!")
 
    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, dev_loader, **kwargs):
        assert self.metric is not None
 
        # 将模型设置为评估模式
        self.model.eval()
 
        global_step = kwargs.get("global_step", -1)
 
        # 用于统计训练集的损失
        total_loss = 0
 
        # 重置评价
        self.metric.reset()
 
        # 遍历验证集每个批次
        for batch_id, data in enumerate(dev_loader):
            X, y = data
 
            # 计算模型输出
            logits = self.model(X)
 
            # 计算损失函数
            loss = self.loss_fn(logits, y).item()
            # 累积损失
            total_loss += loss
 
            # 累积评价
            self.metric.update(logits, y)
 
        dev_loss = (total_loss / len(dev_loader))
        dev_score = self.metric.compute()
 
        # 记录验证集loss
        if global_step != -1:
            self.dev_losses.append((global_step, dev_loss))
            self.dev_scores.append(dev_score)
 
        return dev_score, dev_loss
 
    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, x, **kwargs):
        # 将模型设置为评估模式
        self.model.eval()
        # 运行模型前向计算，得到预测值
        logits = self.model(x)
        return logits
 
    def save_model(self, save_path):
        torch.save(self.model.state_dict(), save_path)
 
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)
        # 数据预处理
transforms = Compose([transforms.ToTensor(), Normalize(mean=[0.5], std=[0.5], )])
class IrisDataset(io.Dataset):
    def __init__(self, mode='train', num_train=120, num_dev=15):
        super(IrisDataset, self).__init__()
        # 调用第三章中的数据读取函数，其中不需要将标签转成one-hot类型
        X, y = load_data(shuffle=True)
        if mode == 'train':
            self.X, self.y = X[:num_train], y[:num_train]
        elif mode == 'dev':
            self.X, self.y = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
        else:
            self.X, self.y = X[num_train + num_dev:], y[num_train + num_dev:]
 
    def __getitem__(self, idx):
        return self.X[idx], self.y[idx]
 
    def __len__(self):
        return len(self.y)
class MNIST_dataset(io.Dataset):
    def __init__(self, dataset, transforms, mode='train'):
        self.mode = mode
        self.transforms =transforms
        self.dataset = dataset
 
    def __getitem__(self, idx):
        # 获取图像和标签
        image, label = self.dataset[0][idx], self.dataset[1][idx]
        image, label = np.array(image).astype('float32'), int(label)
        image = Image.fromarray(image.astype('uint8'), mode='L')
        image = self.transforms(image)
        image = torch.squeeze(image, 0)
        image = torch.squeeze(image, 1)
        return image, label
 
    def __len__(self):
        return len(self.dataset[0])
# 读取标签数据集
with open('./train-labels.idx1-ubyte', 'rb') as lbpath:
    labels_magic, labels_num = struct.unpack('>II', lbpath.read(8))
    labels = np.fromfile(lbpath, dtype=np.uint8)
# 读取图片数据集
with open('./train-images.idx3-ubyte', 'rb') as imgpath:
    images_magic, images_num, rows, cols = struct.unpack('>IIII', imgpath.read(16))
    images = np.fromfile(imgpath, dtype=np.uint8).reshape(images_num, rows * cols)
train_images, train_labels = images[:1000], labels[:1000]
dev_images, dev_labels = images[1000:1200], labels[1000:1200]
test_images, test_labels = images[1200:1400], labels[1200:1400]
train_set, dev_set,test_set= [train_images, train_labels], [dev_images, dev_labels],[test_images, test_labels]
print("train_set[0].shape::",train_set[0].shape)
train_dataset = MNIST_dataset(dataset=train_set, transforms=transforms, mode='train')
test_dataset = MNIST_dataset(dataset=test_set, transforms=transforms, mode='test')
dev_dataset = MNIST_dataset(dataset=dev_set, transforms=transforms, mode='dev')
print("train_dataset:",next(iter(train_dataset))[0].shape)
batch_size = 64
train_loader = io.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = io.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = io.DataLoader(test_dataset, batch_size=batch_size)
print("test_loader:",next(iter(test_loader))[0].shape)
lr = 0.2
fnn_model = Model_MLP_L2_V3(input_size=784, output_size=10, hidden_size=6)
# 定义网络
model = fnn_model
# 定义优化器
optimizer = opt.SGD(model.parameters(),lr, )
# 定义损失函数。softmax+交叉熵
loss_fn = F.cross_entropy
metric = Accuracy(is_logist=True)
runner = RunnerV3(model, optimizer, loss_fn, metric)
 
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader,
            num_epochs=50, log_steps=log_steps, eval_steps = eval_steps,
            save_path="best_model.pdparams")
# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
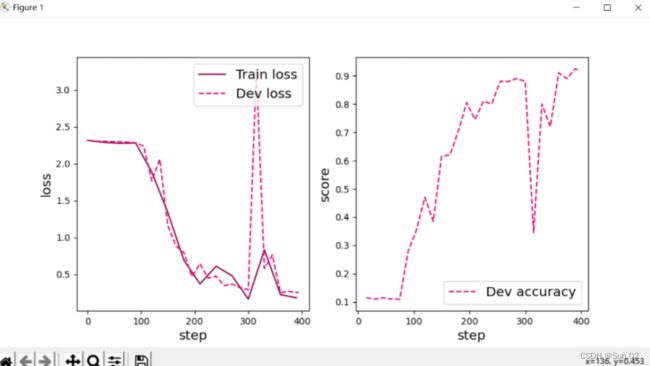
from nndl import Plot_training_loss_acc
Plot_training_loss_acc.plot_training_loss_acc(runner, 'cnn-loss1.pdf')
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))

 总结

本次实验学到了很多新的知识 ，尤其是基于LeNet实现手写体数字识别，对数字识别有了更加清晰的认识，希望再接下来是的实验中学到更多相关内容。