图神经网络(GNNs)模型学习笔记与总结
GCN学习笔记
- 1 基于谱域的GCN
-
- 1.1 知识要点:
- 1.2 Spectral-based models
-
- 1.2.1 Spectral Network
- 1.2.2 ChebNet(2016)
- 1.2.3 GCN(2017)
- 1.2.4 AGCN(2018)
- 1.2.5 DGCN(2018)
- 1.2.6 GWNN
- 1.2.7 小结
- 2 基于空间的GCN
-
- 2.1 知识要点
- 2.2 Spatial-based models
-
- 2.2.1 Neural FPs
- 2.2.2 DCNN
- 2.2.2 PATCHY-SAN
- 2.2.3 GraphSAGE
- 2.2.4 LGCN
- 2.2.5 小结
- 3 基于注意力机制的GCN
-
- 3.1 知识要点
- 3.2 Attention-based spatial models
-
- 3.2.1 GAT
- 3.2.2 GaAN
- 参考文献:
1 基于谱域的GCN
1.1 知识要点:
在spectral-based GCN模型中,会将每个节点的输入看作是信号,并且在进行卷积操作之前,会利用转置后的归一化拉普拉斯矩阵的特征向量将节点的信号进行傅里叶变换,卷积完了之后再用归一化拉普拉斯矩阵的特征向量转换回来。其中,将信号进行傅里叶变换的公式如下:
F ( x ) = U T x F(x)=U^Tx F(x)=UTx
F − 1 ( x ) = U x F^{-1}(x) = Ux F−1(x)=Ux
其中, U U U为归一化拉普拉斯矩阵 L = I N − D − 1 / 2 A D − 1 / 2 L=I_N-D^{-1/2}AD^{-1/2} L=IN−D−1/2AD−1/2的特征向量。基于卷积理论,卷积操作被定义为:
g x = F − 1 ( F ( g ) F ( x ) ) = U ( U T g U T x ) , g x=F^{-1}(F(g) F(x))=U(U^TgU^Tx), gx=F−1(F(g)F(x))=U(UTgUTx),
其中, U T g U^Tg UTg为谱域的过滤器,若将 U T g U^Tg UTg简化为一个可学习的对角矩阵 g w g_w gw,则有
g x = U g w U T x g x=Ug_wU^Tx gx=UgwUTx.
1.2 Spectral-based models
1.2.1 Spectral Network
该模型的思想是直接将 g w g_w gw转换为一个参数对角矩阵 g w = d i a g ( w ) g_w=diag(w) gw=diag(w),这种策略显然是较为低效,且非空间定位的。
1.2.2 ChebNet(2016)
ChebNet的思想就是利用切比雪夫多项式来作为参数,得到
g x = ∑ k = 0 K w k T k ( L ~ ) x gx=\sum_{k=0}^K w_kT_k(\widetilde{L}) x gx=k=0∑KwkTk(L )x,
其中, T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) , T 0 ( x ) = 1 , T 1 ( x ) = x T_k(x) =2xT_{k-1}(x)-T_{k-2}(x), T_0(x)=1,T_1(x)=x Tk(x)=2xTk−1(x)−Tk−2(x),T0(x)=1,T1(x)=x, L ~ = 2 λ m a x L − I N \widetilde{L}=\frac{2}{\lambda_{max}}L-I_N L =λmax2L−IN, λ m a x \lambda_{max} λmax为 L L L的最大特征值。
1.2.3 GCN(2017)
GCN在ChebNet的基础上,令 K = 1 K=1 K=1, λ m a x ≈ 2 \lambda_{max} \approx 2 λmax≈2,得到
g w x = w 0 x + w 1 L ~ x g_w x = w_0x+w_1 \widetilde{L} x gwx=w0x+w1L x,其中, L ~ \widetilde{L} L 被简化为了 D − 1 / 2 A D − 1 / 2 D^{-1/2}AD^{-1/2} D−1/2AD−1/2,得到
g w x = w ( I N + D − 1 / 2 A D − 1 / 2 ) x g_w x=w(I_N+D^{-1/2}AD^{-1/2})x gwx=w(IN+D−1/2AD−1/2)x,令 I N + D − 1 / 2 A D − 1 / 2 = D ~ − 1 / 2 A ~ D ~ − 1 / 2 I_N+D^{-1/2}AD^{-1/2} = \widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2} IN+D−1/2AD−1/2=D −1/2A D −1/2,得到
H = D ~ − 1 / 2 A ~ D ~ − 1 / 2 X W H=\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2}XW H=D −1/2A D −1/2XW
其中, X ∈ R N × F X \in R^{N \times F} X∈RN×F为输入,即节点的特征矩阵, W ∈ R F × F ′ W\in R^{F \times F'} W∈RF×F′为参数, F ′ F' F′为第一层输出size。
1.2.4 AGCN(2018)
AGCN的出发点为:除了已有的节点之间的关系外,在处理不同的任务时节点之间可能还会存在一些潜在的关系,这些信息是有价值的,但GCN则没有考虑这些信息。AGCN通过学得一个残差图拉普拉斯矩阵,并将其加入到拉普拉斯矩阵中来对图拉普拉斯矩阵进行补充。具体地,计算残差图拉普拉斯矩阵首先要计算节点之间的距离,由马氏距离计算得到
D ( x i , x j ) = ( x i − x j ) T M ( x i − x j ) , D(x_i,x_j)=\sqrt{(x_i-x_j)^TM(x_i-x_j)}, D(xi,xj)=(xi−xj)TM(xi−xj),
其中, M = W d W d T M=W_dW_d^T M=WdWdT, W d W_d Wd为参数矩阵(注意:这里使用马氏距离是因为对图结构数据,欧式距离无法准确的度量数据之间的相似性);接着基于马氏距离进行高斯核的映射得到
G ( x i , x j ) = e − D ( x i , x j ) 2 σ 2 G(x_i,x_j)=e^{-\frac{D(x_i,x_j)}{2\sigma ^2}} G(xi,xj)=e−2σ2D(xi,xj)
其中, G ( x i , x j ) G(x_i,x_j) G(xi,xj)为残差邻接矩阵 A r e s A_{res} Ares中第 i i i行,第 j j j列的值,根据 A r e s A_{res} Ares可以计算出 L r e s = I D + D r e s − 1 2 A r e s D r e s − 1 2 L_{res}=I_D+D_{res}^{-\frac{1}{2}}A_{res}D_{res}^{-\frac{1}{2}} Lres=ID+Dres−21AresDres−21。对原始的图拉普拉斯矩阵进行补充调整,有
L ^ = L + α L r e s , \hat{L} = L+\alpha L_{res}, L^=L+αLres,其中, α \alpha α为自由参数。
AGCN最大的贡献就是上面这个残差图拉普拉斯矩阵,该矩阵很好地将潜在的节点关系引入了进来。基于此AGCN的结构如下:
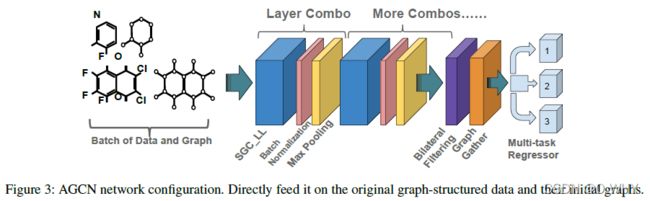
SGC-LL: 传统的CNN中,第 t t t层的输出是第 t − 1 t-1 t−1层所有特征映射的加和,其中特征映射都是用独立的滤波器计算出来的。这意味着新的特征不仅仅只是基于邻居节点建立的,同时也考虑了节点内其他的特征。但在图卷积中,为不同的节点特征创建或训练独立的拓扑结构是难以解释的。因此为了构建节点内和节点间的特征映射,加入了一个转换矩阵和一个bias向量 Y = ( g θ ( L ^ ) X ) W + b Y = (g_{\theta}(\hat{L} )X)W+b Y=(gθ(L^)X)W+b,其中SGC-LL层的训练参数为M、W、b
Max pooling: 对于节点 i i i的第 j j j个特征,经过maxpooling之后,该特征的值为其自身和其邻居节点中在该特征上的最大值, x ^ v ( j ) = m a x ( { x v ( j ) , x i ( j ) , } ) \hat{x}_v(j)=max(\{x_v(j),x_i(j),\}) x^v(j)=max({xv(j),xi(j),})。
Bilateral filtering: 该层用于防止过拟合的发生。
Graph gather: 一个用于表示图的嵌入向量,该向量中的第 i i i个元素是所有节点第 i i i个特征的值之和。
1.2.5 DGCN(2018)
DGCN(Dual-GCN)的出发点为:前人的工作只考虑了节点的局部信息(距离近的节点通常有相同的标签),但是没有考虑到全局信息(出现在类似背景下的节点通常有相同的标签)。作者通过引入一个PPMI矩阵来捕获节点的全局信息,其中每个输入样本都会经过两种类型的卷积神经网络。基于Karate club network的可视化展示如下

基于局部一致性的模型缺陷在于,其认为距离较近的节点更有可能包含相似的标签,如上图中(a)子图的节点8和节点30虽然相连,但他们属于不同的类别。子图(d)是利用GCN将节点进行了映射,然后用t-SNE进行降维后的可视化结果,可见节点8和节点30的位置非常接近。将邻接矩阵中A[30,8],A[8,30]设为0,可以明显的看到节点8和节点30的距离就远了很多。随之而来的一个问题就是:如何自动的减少这种类似情况的发生? DGCN就利用PPMI矩阵来捕获节点的全局信息来缓解这一问题。
首先,PPMI矩阵的计算流程如下:1)首先获得一个频率矩阵F,伪代码如下

Eq.(8)为 p ( s ( t + 1 ) = x j ∣ s ( t ) = x i ) = A i , j ∑ j A i , j p(s(t+1)=x_j|s(t)=x_i)= \frac{A_{i,j}}{\sum_j A_{i,j}} p(s(t+1)=xj∣s(t)=xi)=∑jAi,jAi,j;
2)计算PPMI矩阵

本质上,DGCN其实就是让每个节点都经过两个卷积神经网络,一个是GCN,另一个就是将归一化图拉普拉斯矩阵替换为PPMI矩阵,并且在训练中这两个矩阵共享参数,结构如下

具体地,DGCN致力于解决半监督节点分类问题,其在损失函数中引入了一个正则项,得到损失函数为
L o s s = L 0 + λ ( t ) L r e g , Loss=L_0+\lambda(t)L_{reg}, Loss=L0+λ(t)Lreg,其中, L 0 = − 1 ∣ y L ∣ ∑ l ∈ y L ∑ i = 1 c Y l , i l n Z ^ l , i A L_0=-\frac{1}{|y_L|}\sum_{l\in y_L}\sum_{i=1}^cY_{l,i}ln\hat{Z}_{l,i}^A L0=−∣yL∣1∑l∈yL∑i=1cYl,ilnZ^l,iA, y L y_L yL为给定标签的索引集合, Y Y Y为真正的标签, c c c为类别总数。实际上就是一个交叉熵损失; L r e g = 1 n ∑ i = 1 n ∣ ∣ Z ^ i , : P − Z ^ i , : A ∣ ∣ 2 L_{reg}=\frac{1}{n}\sum_{i=1}^n||\hat{Z}_{i,:}^P-\hat{Z}_{i,:}^A||^2 Lreg=n1∑i=1n∣∣Z^i,:P−Z^i,:A∣∣2为正则化项,属于无监督学习,目的在于使 C o n v P Conv_P ConvP预测出来的结果与 C o n v A Conv_A ConvA的得结果相同。 λ ( t ) \lambda(t) λ(t)的作用在于动态的调节学习率,使得损失函数一开始主要取决于监督学习项,然后再加大 λ ( t ) \lambda(t) λ(t)使模型考虑 C o n v P Conv_P ConvP的信息。
1.2.6 GWNN
GWNN将傅里叶变换替换为了wavelet变换,优点在于1)无需进行矩阵分解就可以得到图wavelet;2)图wavelet是系数且局部的,所以结果更好且解释性更强。
1.2.7 小结
AGCN和DGCN都是希望通过扩充图拉普拉斯矩阵来提高GCN的准确率,GWNN是希望了通过改变信号转换方式来提高性能。但是,以上这些spectral-based模型都是基于图结构的,当图结构发生改变后有需要进行重新训练。
2 基于空间的GCN
2.1 知识要点
基于空间的GCN直接将卷积定义在图上,其关键挑战在于如何在保证CNN的局部不变性情况下,针对不同大小邻域定义卷积操作。
2.2 Spatial-based models
2.2.1 Neural FPs
Nueral FPs为度不同的节点分别设置了不同的参数矩阵
t = h v t + ∑ u ∈ N v h u t t=h_v^t+\sum_{u \in N_v}h_u^t t=hvt+u∈Nv∑hut
h v t + 1 = σ ( t W ∣ N v ∣ t + 1 ) h_v^{t+1}= \sigma(tW^{t+1}_{|N_v|}) hvt+1=σ(tW∣Nv∣t+1)
其中, W ∣ N v ∣ t + 1 W^{t+1}_{|N_v|} W∣Nv∣t+1为 t + 1 t+1 t+1层节点度为 ∣ N v ∣ |N_v| ∣Nv∣的参数矩阵。其缺陷在于当该方法应用在了大规模网络时,计算复杂度会过高。
2.2.2 DCNN
DCNN利用转换矩阵来定义节点的邻域,在节点分类任务中,每个节点的diffusion表示为
H = f ( W c P ∗ X ) ∈ R N × K × F , H=f(W_c P^*X) \in R^{N \times K \times F}, H=f(WcP∗X)∈RN×K×F,
其中, P ∗ = { P , P 2 , P 3 , . . . , P K } P^*=\{P,P^2,P^3,...,P^K\} P∗={P,P2,P3,...,PK}, P P P是由邻接矩阵得到的度归一化转换矩阵。
2.2.2 PATCHY-SAN
PATCHY-SAN的思想是提取每个节点固定大小的邻居节点集合,然后将该邻居网络作为CNN的感受野
2.2.3 GraphSAGE
GraphSAGE是一个经典的inductive模型,该模型的目的在于训练出一个邻居信息聚合器,以使其可以利用在其他网络当中。具体的,该方法通过在一个节点的邻域内采样和聚合特征来生成节点的嵌入表示
h N v t + 1 = A G G t + 1 ( { h u t , u ∈ N v } ) h^{t+1}_{N_v}=AGG_{t+1}(\{h^t_u, u \in N_v\}) hNvt+1=AGGt+1({hut,u∈Nv})
h v t + 1 = σ ( W t + 1 [ h v t ∣ ∣ h N v t + 1 ] ) h^{t+1}_v=\sigma(W^{t+1} [h^t_v || h^{t+1}_{N_v}] ) hvt+1=σ(Wt+1[hvt∣∣hNvt+1])
其中,这里的aggregator可以是均值、LSTM或者池化。
2.2.4 LGCN
LGCN将CNN视为一个aggregator,通过在节点的邻域矩阵上进行最大池化操作以获取top-k特征元素,然后利用一维的CNN来计算隐藏层的表示。
2.2.5 小结
基于空间的方法在利用领域信息上的技巧比较多。此外,这类方法中不再只局限于transductive,有更多的inductive方法。
3 基于注意力机制的GCN
3.1 知识要点
注意力机制在机器翻译、机器阅读等领域取得了巨大的成功。基于注意力机制的GCN与先前两类方法不同,其会为不同的邻居赋予不同的权重。
3.2 Attention-based spatial models
3.2.1 GAT
GAT将注意力机制应用在了propagation step,通过关注每个节点的邻居来生成节点的隐藏层状态
h v t + 1 = p ( ∑ u ∈ N v a v u W h u t ) , h^{t+1}_v = p(\sum_{u \in N_v}a_{vu}Wh^t_u), hvt+1=p(u∈Nv∑avuWhut),
a v u = e x p ( L e a k y R e L U ( a T [ W h v ∣ ∣ W h u ] ) ) ∑ k ∈ N v e x p ( L e a k y R e L U ( a T [ W h v ∣ ∣ W h k ] ) ) a_{vu}=\frac{exp(LeakyReLU(a^T[Wh_v || Wh_u]))}{\sum_{k \in N_v}exp(LeakyReLU(a^T[Wh_v || Wh_k]))} avu=∑k∈Nvexp(LeakyReLU(aT[Whv∣∣Whk]))exp(LeakyReLU(aT[Whv∣∣Whu]))
其中, W W W为参数矩阵, a a a为单层神经网络的参数向量。GAT利用多头注意力来使学习过程变得稳定,其使用K个独立的注意力头矩阵来计算隐藏层,接着将其特征进行组合
h v t + 1 = ∣ ∣ k = 1 K σ ( ∑ u ∈ N v a v u k W k h u t ) , h^{t+1}_v =||_{k=1}^{K} \sigma(\sum_{u \in N_v}a^k_{vu}W_kh^t_u), hvt+1=∣∣k=1Kσ(u∈Nv∑avukWkhut),
h v t + 1 = σ ( 1 K ∑ k = 1 K ∑ u ∈ N v a v u k W k h u t ) h^{t+1}_v =\sigma(\frac{1}{K} \sum_{k=1}^K\sum_{u \in N_v}a^k_{vu}W_kh^t_u) hvt+1=σ(K1k=1∑Ku∈Nv∑avukWkhut)
特点:1)节点-邻居对的计算是并行的,所以有较高的效率;2)可用于具有不同度值的节点;3)可用于inductive学习。
3.2.2 GaAN
GaAN将GAT在组合多头特征时的均值操作改为了基于self-attention机制的操作。
参考文献:
[1] Graph neural networks: A review of methods and applications.
