周志华《机器学习》(西瓜书) —— 学习笔记:第2章 模型评估与选择
文章目录
- 2.1 经验误差和过拟合
- 2.2评估方法
-
- 2.2.1 留出法
- 2.2.2 交叉验证法
- 2.2.3 自助法
- 2.2.4 调参与最终模型
- 2.3 性能度量
-
- 2.3.1 错误率与精度
- 2.3.2 查准率、查全率与 F1
- 2.3.3 ROC 与 AUC
- 2.3.4 代价敏感错误率与代价曲线
- 2.4 比较检验
-
- 2.4.1 假设检验
- 2.4.2 交叉验证 *t* 检验
- 2.4.3 McNemar检验
- 2.4.4 Friedman 检验与 Nemenyi 后续检验
- 2.5 偏差与方差
2.1 经验误差和过拟合
错误率(error rate):分类错误的样本数占样本总数的比例,即如果在 m m m 个样本中有 a a a 个样本分类错误,则错误率 E = a / m E=a/m E=a/m
精度(accuracy): 1 − a / m 1-a/m 1−a/m ,即“精度=1-错误率”,精度常写为百分比的形式 ( 1 − a m ) × 100 % (1-\frac{a}{m})×100\% (1−ma)×100%
误差(error):学习器的实际预测输出与样本的真实输出之间的差异
训练误差(training error)/ 经验误差(empirical error):学习器在训练集上的误差
泛化误差(generalization error):在新样本上的误差
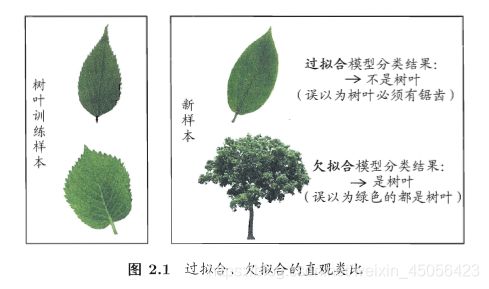
过拟合(overfitting):学习器把训练样本学得“太好”,把训练样本自身的一些特点当作所有潜在样本都具有的一般性质,导致泛化性能下降,这种现象在机器学习中称为“过拟合”
欠拟合(underfitting):对训练样本的一般性质尚未学好
过拟合是机器学习面临的关键障碍,各类学习算法都必然带有一些针对过拟合的措施。过拟合是无法彻底避免的,只能“缓解”或者减小其风险。
2.2评估方法
通常,我们使用一个“测试集”(testing set)来测试学习器对新样本的判别能力,以测试集上的“测试误差”(testing error)作为泛化误差的近似。我们假设测试样本也是从样本真实分布中独立同分布采样而得。要注意测试集应该尽可能与训练集互斥,即测试样本尽量不在训练集中出现、未在训练过程中使用过,否则将得到过于“乐观”的估计结果。
对于一个包含 m m m 个样例的数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D=\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\right.\left(\boldsymbol{x}_{m}, y_{m}\right) \} D={(x1,y1),(x2,y2),…,(xm,ym)} ,通过对 D D D 进行适当的处理,从中产生出训练集 S S S 和测试集 T T T 。下面介绍几种常见的做法。
2.2.1 留出法
“留出法”直接将数据集 D D D 划分为两个互斥的集合,其中一个集合作为训练集 S S S ,另一个作为测试集 T T T ,即 D = S ∪ T D=S \cup T D=S∪T , S ∩ T = ∅ S \cap T=\varnothing S∩T=∅ 。在 S S S 上训练出模型后,用 T T T 来评估其测试误差,作为对泛化误差的估计。
注意一:训练/测试集的划分要尽可能保持数据分布的一致性,避免因数据划分过程引入额外的偏差而对最终结果产生影响。使用“分层采样”(stratified sampling)(保留类别比例的采样方式)。
注意二:单次使用留出法得到的估计结果往往不够稳定可靠,在使用留出法时,一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
通常将大约 2 / 3 ∼ 4 / 5 2/3\sim4/5 2/3∼4/5 的样本用于训练,剩余样本用于测试。
2.2.2 交叉验证法
“交叉验证法”(cross validation)先将数据集 D D D 划分为 k k k 个大小相似的互斥子集,即 D = D 1 ∪ D 2 ∪ … ∪ D k , D i ∩ D j = ∅ ( i ≠ j ) D=D_{1} \cup D_{2} \cup \ldots \cup D_{k}, D_{i} \cap D_{j}=\varnothing\ (i \neq j) D=D1∪D2∪…∪Dk,Di∩Dj=∅ (i=j) ,每个子集 D i D_i Di 尽可能保持数据分布的一致性(即从 D D D 中分层采样得到),每次使用 k − 1 k-1 k−1 个子集的并集作为训练集,余下的那个子集作为测试集。这样可获得 k k k 组训练/测试集,从而进行 k k k 次训练和测试,最终返回的是这 k k k 个测试结果的均值。
交叉验证法评估结果的稳定性和保真性在很大程度上取决于 k k k 的取值,通常把交叉验证法称为“ k k k 折交叉验证”( k k k-fold cross validation)。 k k k 最常用的取值是 10 ,此时称为 10 折交叉验证,其他常用值还有 5 、 20 等。
为减小因样本划分不同而引入的差别, k k k 折交叉验证通常要随机使用不同的划分重复 p p p 次,最终评估结果是这 p p p 次 k k k 折交叉验证结果的均值,如常见的“10 次 10 折交叉验证”(“10 次 10 折交又验证法”与“100 次留出法”都是进行了 100 次训练/测试)。
“留一法(Leave-One-Out,简称LOO)”:交叉验证法的特例,数据集 D D D 中包含 m m m 个样本,同时令 k = m k=m k=m。留一法不受随机样本划分方式的影响,因为 m m m 个样本只有唯一的方式划分为 m m m 个子集——每个子集包含一个样本,使用的训练集与初始数据集相比只少了一个样本。在绝大多数情况下,留一法中被实际评估的模型与期望评估的用 D D D 训练出的模型很相似,评估结果往往被认为比较准确。缺陷是在数据集比较大时,训练 m m m 个模型的计算开销可能是难以忍受的。
2.2.3 自助法
“自助法”(bootstrapping),亦称“可重复采样”或“有放回采样”,直接以自助采样法(bootstrap sampling)为基础。给定包含 m m m 个样本的数据集 D D D ,每次随机从 D D D 中挑选一个样本,将其拷贝放入 D ′ D^{\prime} D′ ,然后将该样本放回初始数据集 D D D 中,该样本在下次采样时仍有可能被采到。这个过程重复执行 m m m 次,可得到包含 m m m 个样本的数据集 D ′ D^{\prime} D′ ,这就是自助采样的结果。 D D D 中有一部分样本会在 D ′ D^{\prime} D′ 中多次出现,另一部分样本不出现。可以估计,样本在 m m m 次采样中始终不被采到的概率是 ( 1 − 1 m ) m \left(1-\frac{1}{m}\right)^{m} (1−m1)m ,取极限得到
lim m → ∞ ( 1 − 1 m ) m ↦ 1 e ≈ 0.368 (2.1) \lim _{m \rightarrow \infty}\left(1-\frac{1}{m}\right)^{m} \mapsto \frac{1}{e} \approx 0.368\tag{2.1} m→∞lim(1−m1)m↦e1≈0.368(2.1)
即通过自助采样,初始数据集 D D D 中约有 36.8 36.8% 36.8 的样本未出现在采样数据集 D ′ D^{\prime} D′ 中。我们可将 D ′ D^{\prime} D′ 用作训练集, D \ D ′ D \backslash D^{\prime} D\D′ 用作测试集。这样,实际评估的模型与期望评估的模型都使用 m m m 个训练样本,还有占数据总量约 1/3 的、没在训练集中出现的样本用于测试。这样的测试结果亦称“包外估计”(out-of-bag-estimate)。
自助法在数据集较小、难以有效划分训练/测试集时很有用;自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法有很大的好处。然而,自助法产生的数据集改变了初始数据集的分布,这会引入估计偏差。因此,在初始数据量足够时,留出法和交叉验证法更常用一些。
2.2.4 调参与最终模型
在进行模型评估与选择时,除了要对适用学习算法进行选择,还需对算法参数进行设定,这就是通常所说的“参数调节”或简称“调参”(parameter tuning)。
现实中常用的做法,是对每个参数选定一个范围和变化步长,例如在 [ 0 , 0.2 ] [0,0.2] [0,0.2] 范围内以 0.05 0.05 0.05 为步长,则实际要评估的候选参数值有 5 5 5 个,最终是从这 5 5 5 个候选值中产生选定值。这样选定的参数值往往不是“最佳”值,但这是在计算开销和性能估计之间进行折中的结果。通过这个折中,使学习过程变得可行。在不少应用任务中,参数调得好不好往往对最终模型性能有关键性影响。
在模型评估与选择过程中需要留出部分数据进行评估测试,我们事实上只使用了一部分数据训练模型。因此,在模型选择完成后,学习算法和参数配置已选定,我们应该用完整的数据集重新训练模型。这个模型在训练过程中使用了所有的样本,这才是我们最终提交给用户的模型。
另外,我们通常把学得模型在实际使用中遇到的数据称为测试数据,而在模型评估与选择中用于评估测试的数据集常称为“验证集”(validation set)。例如,在研究对比不同算法的泛化性能时,我们用测试集上的判别效果来估计模型在实际使用时的泛化能力,而把训练数据另外划分为训练集和验证集,基于验证集上的性能来进行模型选择和调参。
2.3 性能度量
“性能度量”(performance measure)是衡量模型泛化能力的评价标准。性能度量反映了任务需求,在对比不同模型的能力时,使用不同的性能度量往往会导致不同的评判结果。模型的“好坏”是相对的,它不仅取决于算法和数据,还取决于任务需求。
在预测任务中,给定样例集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D=\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\} D={(x1,y1),(x2,y2),…,(xm,ym)} ,其中 y i y_i yi 是示例 x i \boldsymbol{x}_{i} xi 的真实标记。要评估学习器 f f f 的性能,就要把学习器预测结果 f ( x ) f(\boldsymbol{x}) f(x) 与真实标记 y \boldsymbol{y} y 进行比较。
回归任务最常用的性能度量是“均方误差”(mean squared error)
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 (2.2) E(f ; D)=\frac{1}{m} \sum_{i=1}^{m}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2}\tag{2.2} E(f;D)=m1i=1∑m(f(xi)−yi)2(2.2)
更一般的,对于数据分布 D \mathcal{D} D 和概率密度函数 p ( ⋅ ) p(\cdot) p(⋅) ,均方误差可描述为
E ( f ; D ) = ∫ x ∼ D ( f ( x ) − y ) 2 p ( x ) d x (2.3) E(f ; \mathcal{D})=\int_{\boldsymbol{x} \sim \mathcal{D}}(f(\boldsymbol{x})-y)^{2} p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}\tag{2.3} E(f;D)=∫x∼D(f(x)−y)2p(x)dx(2.3)
以下主要介绍分类任务中常用的性能度量。
2.3.1 错误率与精度
错误率和精度是分类任务中最常用的两种性能度量,既适用于二分类任务,也适用于多分类任务。错误率是分类错误的样本数占样本总数的比例,精度则是分类正确的样本数占样本总数的比例。对样例集 D D D ,分类错误率定义为
E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) (2.4) E(f ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right)\tag{2.4} E(f;D)=m1i=1∑mI(f(xi)=yi)(2.4)
精度则定义为
acc ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) = 1 − E ( f ; D ) (2.5) \begin{aligned} \operatorname{acc}(f ; D) &=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right)=y_{i}\right) \\\\ &=1-E(f ; D) \end{aligned}\tag{2.5} acc(f;D)=m1i=1∑mI(f(xi)=yi)=1−E(f;D)(2.5)
更一般的,对于数据分布 D \mathcal{D} D 和概率密度函数 p ( ⋅ ) p(\cdot) p(⋅) ,错误率与精度可分别描述为
E ( f ; D ) = ∫ x ∼ D I ( f ( x ) ≠ y ) p ( x ) d x (2.6) E(f ; \mathcal{D})=\int_{\boldsymbol{x} \sim \mathcal{D}} \mathbb{I}(f(\boldsymbol{x}) \neq y) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}\tag{2.6} E(f;D)=∫x∼DI(f(x)=y)p(x)dx(2.6)
acc ( f ; D ) = ∫ x ∼ D I ( f ( x ) = y ) p ( x ) d x = 1 − E ( f ; D ) (2.7) \begin{aligned} \operatorname{acc}(f ; \mathcal{D}) &=\int_{x \sim D} \mathbb{I}(f(\boldsymbol{x})=y) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \\\\ &=1-E(f ; \mathcal{D}) \end{aligned}\tag{2.7} acc(f;D)=∫x∼DI(f(x)=y)p(x)dx=1−E(f;D)(2.7)
2.3.2 查准率、查全率与 F1
在信息检索中,我们经常会关心“检索出的信息中有多少比例是用户感兴趣的”、“用户感兴趣的信息中有多少被检索出来了”,“查准率”(“准确率”)(precision)与“查全率”(“召回率”)(recall)是适用于此类需求的性能度量。
对于二分类问题,将样例根据其真实类别与学习器预测类别的组合,划分为真正例(true positive)、假正例(false positive)、真反例(true negative)、假反例(false negative)四种情形,分别用 T P 、 F P 、 T N 、 F N TP、FP、TN、FN TP、FP、TN、FN 表示其对应的样例数,则 T P + F P + T N + F N TP+FP+TN+FN TP+FP+TN+FN = 样例总数 。分类结果的“混淆矩阵”(confusion matrix)如表 2.1 所示
查准率 P P P 与查全率 R R R 分别定义为
P = T P T P + F P (2.8) P=\frac{TP}{TP+FP}\tag{2.8} P=TP+FPTP(2.8)
R = T P T P + F N (2.9) R=\frac{TP}{TP+FN}\tag{2.9} R=TP+FNTP(2.9)
查准率和查全率是一对矛盾的度量。一般查准率高时,查全率往往偏低;而查全率高时,查准率往往偏低。例如,若希望将好瓜尽可能多地选出来,则可通过增加选瓜的数量来实现,如果将所有西瓜都选上,那么所有的好瓜也必然都被选上了,但这样查准率就会较低;若希望选出的瓜中好瓜比例尽可能高,则可只挑选最有把握的瓜,但这样就难免会漏掉不少好瓜,使得查全率较低。通常只有在一些简单任务中,才可能使查全率和查准率都很高。
根据学习器的预测结果对样例进行排序,“最可能”是正例的样本排在前面,“最不可能”是正例的样本排在最后,按此顺序逐个把样本作为正例进行预测,每次计算出当前的查全率、查准率,以查准率为纵轴、查全率为横轴作图,就得到查准率-查全率曲线,简称“P-R 曲线”,显示该曲线的图称为“P-R 图”。
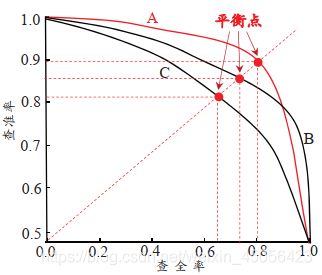
若一个学习器的 P-R 曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者,例如图2.3中学习器 A 的性能优于学习器 C 。如果两个学习器的 P-R 曲线发生了交叉,例如图2.3中的 A 与 B ,则只能在具体的查准率或查全率条件下进行比较。如果仍希望把学习器 A 与 B 比出个高低,一个比较合理的判断依据是,比较 P-R 曲线下面积的大小,它在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。这个值不太容易估算,因此,人们设计了一些综合考虑查准率、查全率的性能度量。
“平衡点”(Break-Event Point,简称 BEP)就是这样一个度量,它是“查准率=查全率”时的取值,例如图 2.3 中学习器 C 的 BEP 是0.64,而基于 BEP 的比较,可认为学习器 A 优于 B 。
但 BEP 过于简化,更常用的是 F 1 F1 F1 度量:
F 1 = 2 × P × R P + R = 2 × T P 样 例 总 数 + T P − T N (2.10) F 1=\frac{2 \times P \times R}{P+R}=\frac{2 \times TP}{样例总数+TP-TN}\tag{2.10} F1=P+R2×P×R=样例总数+TP−TN2×TP(2.10)
在一些应用中,对查准率和查全率的重视程度有所不同。例如在商品推荐系统中,为了尽可能少打扰用户,更希望推荐内容的确是用户感兴趣的,此时查准率更重要;而在逃犯信息检索系统中,更希望尽可能少漏掉逃犯,此时查全率更重要。 F 1 F1 F1 度量的一般形式—— F β F_\beta Fβ ,能让我们表达出对查准率/查全率的不同偏好,它定义为
F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R (2.11) F_{\beta}=\frac{\left(1+\beta^{2}\right) \times P \times R}{\left(\beta^{2} \times P\right)+R}\tag{2.11} Fβ=(β2×P)+R(1+β2)×P×R(2.11)
其中 β > 0 \beta > 0 β>0 度量了查全率对查准率的相对重要性。 β = 1 \beta = 1 β=1 时退化为标准的 F 1 F1 F1 ; β > 1 \beta>1 β>1 时查全率有更大影响; β < 1 \beta < 1 β<1 时查准率有更大影响。
F 1 F1 F1 是基于查准率与查全率的调和平均定义的
1 F 1 = 1 2 ⋅ ( 1 P + 1 R ) \frac{1}{F 1}=\frac{1}{2} \cdot\left(\frac{1}{P}+\frac{1}{R}\right) F11=21⋅(P1+R1)
F β F_{\beta} Fβ 则是加权调和平均
1 F β = 1 1 + β 2 ⋅ ( 1 P + β 2 R ) \frac{1}{F_{\beta}}=\frac{1}{1+\beta^{2}} \cdot\left(\frac{1}{P}+\frac{\beta^{2}}{R}\right) Fβ1=1+β21⋅(P1+Rβ2)
很多时候我们有多个二分类混淆矩阵,我们希望在 n n n 个二分类混淆矩阵上综合考察查准率和查全率。
一种直接的做法是先在各混淆矩阵上分别计算出查准率和查全率,记为 ( P 1 , R 1 ) , ( P 2 , R 2 ) , … , ( P n , R n ) \left(P_{1}, R_{1}\right),\left(P_{2}, R_{2}\right), \ldots,\left(P_{n}, R_{n}\right) (P1,R1),(P2,R2),…,(Pn,Rn) ,再计算平均值,这样就得到“宏查准率”(macro- P P P)、“宏查全率”(macro- R R R),以及相应的“宏 F 1 F1 F1 ”(macro- F 1 F1 F1)
macro- P = 1 n ∑ i = 1 n P i (2.12) \operatorname{macro-}P=\frac{1}{n} \sum_{i=1}^{n} P_{i}\tag{2.12} macro-P=n1i=1∑nPi(2.12)
macro- R = 1 n ∑ i = 1 n R i (2.13) \operatorname{macro-}R=\frac{1}{n} \sum_{i=1}^{n} R_{i}\tag{2.13} macro-R=n1i=1∑nRi(2.13)
macro- F 1 = 2 × macro- P × macro-R macro- P + macro- R (2.14) \operatorname{macro-}F 1=\frac{2 \times \operatorname{macro-} P \times \operatorname{macro-R}}{\operatorname{macro-} P+\operatorname{macro-}R}\tag{2.14} macro-F1=macro-P+macro-R2×macro-P×macro-R(2.14)
还可先将各混淆矩阵的对应元素进行平均,得到 T P 、 F P 、 T N 、 F N TP、FP、TN、FN TP、FP、TN、FN 的平均值,分别记为 T P ‾ 、 F P ‾ 、 T N ‾ 、 F N ‾ \overline{TP}、\overline{FP}、\overline{TN}、\overline{FN} TP、FP、TN、FN ,再基于这些平均值计算出“微查准率”(micro- P P P)、“微查全率”(micro- R R R)和“微 F 1 F1 F1 ”(micro- F 1 F1 F1)
micro- P = T P ‾ T P ‾ + F P ‾ (2.15) \operatorname{micro-} P=\frac{\overline{T P}}{\overline{T P}+\overline{F P}}\tag{2.15} micro-P=TP+FPTP(2.15)
micro- R = T P ‾ T P ‾ + F N ‾ (2.16) \operatorname{micro-} R=\frac{\overline{T P}}{\overline{T P}+\overline{F N}}\tag{2.16} micro-R=TP+FNTP(2.16)
micro- F 1 = 2 × micro- P × micro- R micro- P + micro- R (2.17) \operatorname{micro-}F 1=\frac{2 \times \operatorname{micro-} P \times \operatorname{micro-}R}{\operatorname{micro-}P+\operatorname{micro-}R}\tag{2.17} micro-F1=micro-P+micro-R2×micro-P×micro-R(2.17)
2.3.3 ROC 与 AUC
很多学习器是为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阀值(threshold)进行比较,若大于阈值则分为正类,否则为反类。例如,神经网络在一般情形下是对每个测试样本预测出一个 [ 0.0 , 1.0 ] [0.0,1.0] [0.0,1.0] 之间的实值,然后将这个值与 0.5 进行比较,大于 0.5 则判为正例,否则为反例。这个实值或概率预测结果的好坏,直接决定了学习器的泛化能力。实际上,根据这个实值或概率预测结果,我们可将测试样本进行排序,“最可能”是正例的排在最前面,“最不可能”是正例的排在最后面。这样,分类过程就相当于在这个排序中以某个“截断点”(cut point)将样本分为两部分,前一部分判作正例,后一部分则判作反例。
在不同的应用任务中,我们可根据任务需求来采用不同的截断点,例如若我们更重视“查准率”,则可选择排序中靠前的位置进行截断;若更重视“查全率”,则可选择靠后的位置进行截断。因此,排序本身的质量好坏,体现了综合考虑学习器在不同任务下的“期望泛化性能”的好坏,或者说,“一般情况下”泛化性能的好坏。ROC曲线则是从这个角度出发来研究学习器泛化性能的有力工具。
ROC(Receiver Operating Characteristic):全称“受试者工作特征”曲线,根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算“真正例率”和“假正例率”,分别以它们为横、纵坐标作图,就可得到“ ROC 曲线”。基于表 2.1 中的符号,两者分别定义为
T P R = T P T P + F N (2.18) \mathrm{TPR}=\frac{T P}{T P+F N}\tag{2.18} TPR=TP+FNTP(2.18)
F P R = F P T N + F P (2.19) \mathrm{FPR}=\frac{F P}{T N+F P}\tag{2.19} FPR=TN+FPFP(2.19)
显示 ROC 曲线的图称为“ ROC 图”。图 2.4(a) 是一个示意图。对角线对应于“随机猜测”模型,点 ( 0 , 1 ) (0,1) (0,1) 对应于将所有正例排在所有反例之前的“理想模型”。
现实任务中通常用有限个测试样例绘制 ROC 图,仅能获得有限个 ( 真 正 例 率 , 假 正 例 率 ) (真正例率,假正例率) (真正例率,假正例率) 坐标对,无法产生图 2.4(a) 中的光滑 ROC 曲线,只能绘制出如图 2.4(b) 所示的近似 ROC 曲线。
绘图过程:给定 m + m^+ m+ 个正例和 m − m^- m− 个反例,根据学习器预测结果对样例进行排序,把分类阈值设为最大,即把所有样例均预测为反例,此时真正例率和假正例率均为 0 ,在坐标 ( 0 , 0 ) (0,0) (0,0) 处标记一个点。然后将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为 ( x , y ) (x,y) (x,y) ,当前若为真正例,则对应标记点的坐标为 ( x , y + 1 m + ) \left(x, y+\frac{1}{m^{+}}\right) (x,y+m+1) ,当前若为假正例,则对应标记点的坐标为 ( x + 1 m − , y ) \left(x+\frac{1}{m^{-}}, y\right) (x+m−1,y) ,最后用线段连接相邻点即可。
这里对周老师书中的内容做一点补充,当学习器对多个样例的预测结果相同时,书中并没有做确切说明如何处理。按照前面的绘图方法,若这些样例采用不同的具体方式排序,会画出不同的 ROC 路线。这时我们要这样处理:不论这些预测值相同的样例以何种方式排序,在按照前面的方法进行描点后,直接将前一个不同预测结果的点,与这组预测结果相同的点中的最后一个相连即可。例如,有 10 个样例预测结果相同,其中 6 个正例, 4 个反例。如图 2.5 ,我们用黑点表示这 10 个样例,用红点表示排在它们之前的那个样例。如果对这 10 个样例采用不同的方式排序,得到 ROC 路线是不同的。所以,连线时,我们跳过中间的黑点,直接将红点和最后一个黑点连接,具体情形如图 2.5 中的虚线。
进行学习器比较时,若一个学习器的 ROC 曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者。若两个学习器的 ROC 曲线发生交叉,则难以一般性地断言两者孰优孰劣。此时较为合理的判据是比较 ROC 曲线下的面积,即 AUC(Area Under ROC Curve) ,如图 2.4 所示。
假定 ROC 曲线由坐标为 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } \left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{m}, y_{m}\right)\right\} {(x1,y1),(x2,y2),…,(xm,ym)} 的点按序连接而成 ( x 1 = 0 , x m = 1 ) \left(x_{1}=0, x_{m}=1\right) (x1=0,xm=1) ,如图 2.4(b) ,则 AUC 可估算为
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ⋅ ( y i + y i + 1 ) (2.20) \mathrm{AUC}=\frac{1}{2} \sum_{i=1}^{m-1}\left(x_{i+1}-x_{i}\right) \cdot\left(y_{i}+y_{i+1}\right)\tag{2.20} AUC=21i=1∑m−1(xi+1−xi)⋅(yi+yi+1)(2.20)
AUC 考虑的是样本预测的排序质量,它与排序误差有紧密联系。给定 m + m^+ m+ 个正例和 m − m^- m− 个反例,令 D + D^+ D+ 和 D − D^- D− 分别表示正、反例集合,则排序“损失”定义为
ℓ rank = 1 m + m − ∑ x + ∈ D + ∑ x − ∈ D − ( I ( f ( x + ) < f ( x − ) ) + 1 2 I ( f ( x + ) = f ( x − ) ) ) (2.21) \ell_{\text {rank}}=\frac{1}{m^{+} m^{-}} \sum_{\boldsymbol{x}^{+} \in D^{+}} \sum_{\boldsymbol{x}^{-} \in D^{-}}\left(\mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)
即考虑每一对正、反例,若正例的预测值小于反例,则记一个“罚分”,若相等,则记 0.5 个“罚分”。容易看出 ℓ r a n k \ell_{r a n k} ℓrank 对应的是 ROC 曲线之上的面积:若一个正例在 ROC 曲线上对应标记点的坐标为 ( x , y ) (x,y) (x,y) ,则 x x x 恰是排序在其之前的反例所占的比例,即假正例率。因此有
A U C = 1 − ℓ rank (2.22) \mathrm{AUC}=1-\ell_{\text {rank}}\tag{2.22} AUC=1−ℓrank(2.22)
这里根据自己的思考与理解,对式(2.20)、式(2.21)、式(2.22)做一些说明:
假设我们有 10 个样例, 5 个正例, 5 个反例,按其预测值进行排序得到如下一组结果(其中 ⋅ + \cdot^+ ⋅+ 为正例, ⋅ − \cdot^- ⋅− 为反例):
( 0. 9 + , 0. 8 + , 0. 7 − , 0. 5 + , 0. 5 − , 0. 5 + , 0. 4 − , 0. 3 + , 0. 2 − , 0. 1 − ) (0.9^+,0.8^+,0.7^-,0.5^+,0.5^-,0.5^+,0.4^-,0.3^+,0.2^-,0.1^-) (0.9+,0.8+,0.7−,0.5+,0.5−,0.5+,0.4−,0.3+,0.2−,0.1−)
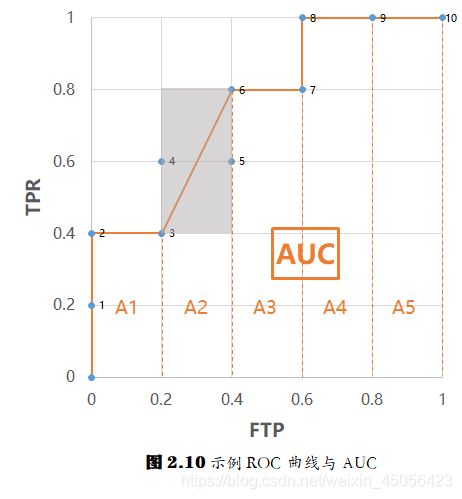
我们先绘制出这组样例的 ROC 曲线,并确定它们的 AUC ,如图 2.10
图中蓝色的点是这组样例对应的描点,橙色的曲线是绘制出的 ROC 曲线,曲线下方的面积,就是 AUC 。
这里, 5 个正例将 y y y 轴平均分成了 5 份, 5 个反例将 x x x 轴平均分成了 5 份。图中的 AUC 值可由式 2.20 算出,不论是形如 A1、A3、A4、A5 的矩形面积( y i = y i + 1 y_{i}=y_{i+1} yi=yi+1),还是形如 A2 的梯形面积( y i ≠ y i + 1 y_{i} \neq y_{i+1} yi=yi+1),都可用公式 1 2 ( x i + 1 − x i ) ( y i + y i + 1 ) \frac{1}{2}(x_{i+1}-x_{i})(y_{i}+y_{i+1}) 21(xi+1−xi)(yi+yi+1) 求得。注意,这里的 ( x i , y i ) (x_i,y_i) (xi,yi) 点不完全是每个样例对应的描点,而是在 ROC 曲线上的那部分样例的描点。
接下来,我们具体理解下: ℓ rank \ell_{\text {rank}} ℓrank 对应的是 ROC 曲线之上的面积。
显然,图 2.10 中每一小格的面积是 1 5 ⋅ 1 5 \frac{1}{5}\cdot\frac{1}{5} 51⋅51 。实际上,若有 m + m^+ m+ 个正例和 m − m^- m− 个反例,它们会分别将 y y y 轴和 x x x 轴平均分成 m + m^+ m+ 份和 m − m^- m− 份,每一小格的面积是 1 m + ⋅ 1 m − \frac{1}{m^+}\cdot\frac{1}{m^-} m+1⋅m−1 ,式(2.21)中的 1 m + m − \frac{1}{m^+m^-} m+m−1 就表示分割后每一小格的面积。
再看 ∑ x + ∈ D + ∑ x − ∈ D − I ( f ( x + ) < f ( x − ) ) \sum_{\boldsymbol{x}^{+} \in D^{+}} \sum_{\boldsymbol{x}^{-} \in D^{-}}\mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)
最后看 ∑ x + ∈ D + ∑ x − ∈ D − 1 2 I ( f ( x + ) = f ( x − ) ) \sum_{\boldsymbol{x}^{+} \in D^{+}} \sum_{\boldsymbol{x}^{-} \in D^{-}}\frac{1}{2} \mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)=f\left(\boldsymbol{x}^{-}\right)\right) ∑x+∈D+∑x−∈D−21I(f(x+)=f(x−)) ,当有 a a a 个正例和 b b b 个反例预测值相同时,必然会在坐标轴上形成一个占据 a × b a \times b a×b 个格子的矩形,这些样例对应的 ROC 曲线,是这个矩形的对角线。这个矩形有一半在 ROC 曲线之上,对应的“格子数”是 1 2 a b \frac{1}{2}ab 21ab 。比如样例 0. 5 + 0.5^+ 0.5+ 、 0. 5 − 0.5^- 0.5− 、 0. 5 + 0.5^+ 0.5+ , 2 个正例和 1 个反例预测值相同,所形成的矩形在 ROC 曲线之上的部分对应的格子数是 1 2 × 2 × 1 = 1 \frac{1}{2} \times 2 \times 1 = 1 21×2×1=1 ,如图 2.10 灰色部分所示。所以, ∑ x + ∈ D + ∑ x − ∈ D − 1 2 I ( f ( x + ) = f ( x − ) ) \sum_{\boldsymbol{x}^{+} \in D^{+}} \sum_{\boldsymbol{x}^{-} \in D^{-}}\frac{1}{2} \mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)=f\left(\boldsymbol{x}^{-}\right)\right) ∑x+∈D+∑x−∈D−21I(f(x+)=f(x−)) 表示的就是 ROC 曲线上方这种不完整格子累计起来的个数。
ROC 曲线上方完整的格子数加上不完整的格子数,再乘以每个格子的面积,就是 ROC 曲线上方的总面积,这就是 ℓ rank \ell_{\text {rank}} ℓrank 对应的是 ROC 曲线之上的面积的原因。这点明确后,式(2.22) 自然就成立了。
2.3.4 代价敏感错误率与代价曲线
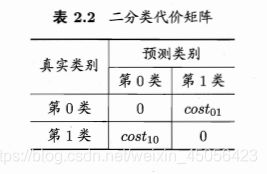
为权衡不同类型错误所造成的不同损失,可为错误赋予“非均等代价”(unequal cost)。以二分类任务为例,我们可根据任务的领域知识设定一个“代价矩阵”(cost matrix),如表 2.2 所示,其中 c o s t i j cost_{ij} costij 表示将第 i i i 类样本预测为第 j j j 类样本的代价。一般来说: c o s t i i = 0 cost_{ii}=0 costii=0 ;若将第 0 类判别为第 1 类所造成的损失更大,则 c o s t 01 > c o s t 10 cost_{01} > cost_{10} cost01>cost10 ;损失程度相差越大, c o s t 01 cost_{01} cost01 与 c o s t 10 cost_{10} cost10 值的差别越大。
前面介绍的性能度量大都隐式地假设均等代价,例如式(2.4)所定义的错误率,是直接计算“错误次数”,并没有考虑不同错误会造成不同的后果。在非均等代价情况下,我们希望最小化“总体代价”(total cost)。若将表 2.2 中的第 0 类作为正类、第 1 类作为反类,令 D + D^+ D+ 与 D − D^- D− 分别代表样例集 D D D 的正例子集和反例子集,则“代价敏感”(cost-sensitive)错误率为
E ( f ; D ; c o s t ) = 1 m ( ∑ x i ∈ D + I ( f ( x i ) ≠ y i ) × cost 01 + ∑ x i ∈ D − I ( f ( x i ) ≠ y i ) × cost 10 ) (2.23) \begin{aligned} E(f ; D ; cost)= \frac{1}{m}\left(\sum_{\boldsymbol{x}_{i} \in D^{+}} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \times \operatorname{cost}_{01} + \sum_{\boldsymbol{x}_{i} \in D^{-}} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \times \operatorname{cost}_{10} \right) \end{aligned}\tag{2.23} E(f;D;cost)=m1(xi∈D+∑I(f(xi)=yi)×cost01+xi∈D−∑I(f(xi)=yi)×cost10)(2.23)
类似可给出基于分布定义的代价敏感错误率,及其他一些性能度量的代价敏感版本。若令 c o s t i j cost_{ij} costij 中的 i i i 、 j j j 取值不限于 0 、 1 ,则可定义出多分类任务的代价敏感性能度量。
在非均等代价下,用“代价曲线”(cost curve)反映学习器的期望总体代价。代价曲线图的横轴是取值为 [ 0 , 1 ] [0,1] [0,1] 的归一化正例概率代价
P ( + ) cost = p × c o s t 01 p × cost 01 + ( 1 − p ) × c o s t 10 (2.24) P(+) \operatorname{cost}=\frac{p \times cost_{01}}{p \times \operatorname{cost}_{01}+(1-p) \times cost_{10}}\tag{2.24} P(+)cost=p×cost01+(1−p)×cost10p×cost01(2.24)
其中 p p p 是样例为正例的概率;纵轴是取值为 [ 0 , 1 ] [0,1] [0,1] 的归一化模型代价
cost n o r m = F N R × p × c o s t 01 + F P R × ( 1 − p ) × c o s t 10 p × c o s t 01 + ( 1 − p ) × c o s t 10 (2.25) \operatorname{cost}_{n o r m}=\frac{\mathrm{FNR} \times p \times cost_{01}+\mathrm{FPR} \times(1-p) \times cost_{10}}{p \times cost_{01}+(1-p) \times cost_{10}}\tag{2.25} costnorm=p×cost01+(1−p)×cost10FNR×p×cost01+FPR×(1−p)×cost10(2.25)
其中 F P R \mathrm{FPR} FPR 是式(2.19)定义的假正例率, F N R = 1 − T P R \mathrm{FNR}=1-\mathrm{TPR} FNR=1−TPR 是假反例率。
代价曲线的绘制:ROC 曲线上每一点对应代价平面上的一条线段,设 ROC 曲线上点的坐标为 ( T P R , F P R ) (\mathrm{TPR},\mathrm{FPR}) (TPR,FPR) ,则可相应计算出 F N R \mathrm{FNR} FNR ,在代价平面上绘制一条从 ( 0 , F P R ) (0,\mathrm{FPR}) (0,FPR) 到 ( 1 , F N R ) (1,\mathrm{FNR}) (1,FNR) 的线段,线段下的面积即表示该条件下的期望总体代价;如此将 ROC 曲线上的每个点转化为代价平面上的一条线段,然后取所有线段的下界,围成的面积即为在所有条件下学习器的期望总体代价,如图 2.5 所示
2.4 比较检验
统计假设检验(hypothesis test)为我们进行学习器性能比较提供了重要依据。基于假设检验结果我们可推断出,若在测试集上观察到学习器 A 比 B 好,则 A 的泛化性能是否在统计意义上优于 B ,以及这个结论的把握有多大。下面我们先介绍两种最基本的假设检验,然后介绍几种常用的机器学习性能比较方法。为便于讨论,本节默认以错误率为性能度量,用 ϵ \epsilon ϵ 表示。
2.4.1 假设检验
泛化错误率为 ϵ \epsilon ϵ 的学习器在一个样本上犯错的概率是 ϵ \epsilon ϵ 。测试错误率 ϵ ^ \hat{\epsilon} ϵ^ 意味着在 m m m 个测试样本中有 ϵ ^ × m \hat{\epsilon}\times m ϵ^×m 个被误分类。假定测试样本从样本总体分布中独立采样而得,泛化错误率为 ϵ \epsilon ϵ 的学习器将其中 m ′ m^{\prime} m′ 个样本误分类,其余样本正确分类的概率是 ϵ m ′ ( 1 − ϵ ) m − m ′ \epsilon^{m^{\prime}}(1-\epsilon)^{m-m^{\prime}} ϵm′(1−ϵ)m−m′ 。恰将 ϵ ^ × m \hat{\epsilon} \times m ϵ^×m 个样本误分类的概率如下式所示,这也表示在包含 m m m 个样本的测试集上,泛化错误率为 ϵ \epsilon ϵ 的学习器被测得测试错误率为 ϵ ^ \hat{\epsilon} ϵ^ 的概率
P ( ϵ ^ ; ϵ ) = ( m ϵ ^ × m ) ϵ ϵ ^ × m ( 1 − ϵ ) m − e ^ × m (2.26) P(\hat{\epsilon} ; \epsilon)=\left(\begin{array}{c}{m} \\ {\hat{\epsilon} \times m}\end{array}\right) \epsilon^{\hat{\epsilon} \times m}(1-\epsilon)^{m-\hat{e} \times m}\tag{2.26} P(ϵ^;ϵ)=(mϵ^×m)ϵϵ^×m(1−ϵ)m−e^×m(2.26)
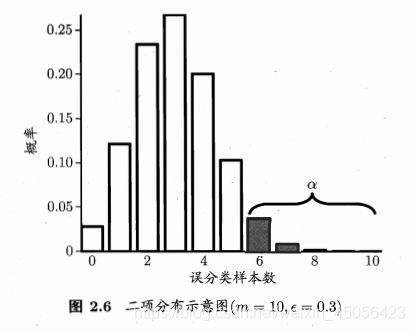
上式解 ∂ P ( ϵ ^ ; ϵ ) / ∂ ϵ = 0 \partial P(\hat{\epsilon} ; \epsilon) / \partial \epsilon=0 ∂P(ϵ^;ϵ)/∂ϵ=0 可知, P ( ϵ ^ ; ϵ ) P(\hat{\epsilon} ; \epsilon) P(ϵ^;ϵ) 在 ϵ = ϵ ^ \epsilon=\hat{\epsilon} ϵ=ϵ^ 时最大, ∣ ϵ − ϵ ^ ∣ |\epsilon-\hat{\epsilon}| ∣ϵ−ϵ^∣ 增大时 P ( ϵ ^ ; ϵ ) P(\hat{\epsilon} ; \epsilon) P(ϵ^;ϵ) 减小。这符合二项分布,如图2.6,若 ϵ = 0.3 \epsilon=0.3 ϵ=0.3 ,则 10 个样本中测得 3 个被误分类的概率最大。
个人认为式(2.27)存在一些不太好理解的问题,所以这里补充一些自己的思考过程,以及对式(2.27)的理解,如有不对之处,欢迎大家指正。
根据式(2.26),计算出泛化错误率为 ϵ = 0.3 \epsilon=0.3 ϵ=0.3 的学习器,对例中样本进行误分类时的误分类样本个数和误分类概率、累积误分类概率的对应关系,整理成下面的表格
| 误分类个数 | 误分类概率 | 累积概率 |
|---|---|---|
| 0 | 0.0282 | 0.0282 |
| 1 | 0.1211 | 0.1493 |
| 2 | 0.2335 | 0.3828 |
| 3 | 0.2668 | 0.6496 |
| 4 | 0.2001 | 0.8497 |
| 5 | 0.1029 | 0.9526 |
| 6 | 0.0368 | 0.9894 |
| 7 | 0.0090 | 0.9984 |
| 8 | 0.0015 | 0.9999 |
| 9 | 0.0001 | 1.0000 |
| 10 | 0.0000 | 1.0000 |
从表格我们可以直观看到,误分类个数为 3 个,即测试错误率为 0.3 的概率值最大。
同时,我们还能注意到,误分类个数达到 4 个、 5 个、 6 个时,累积概率分别是 0.8497 、 0.9526 、 0.9894 ,说明这个学习器有 15.03% 的可能分错 4 个以上的样本,有 4.74% 的可能分错 5 个以上的样本,有 1.06% 的可能分错 6 以上的样本。
在假设检验里,如果我们把显著度定为 5%(即 0.05 ),那么发生概率小于 5% 的事件就属于小概率事件,根据小概率原理,“在一次试验中,小概率事件实际上是不可能发生的”,所以从假设检验的角度说,泛化错误率为 0.3 的学习器,在对 10 个样本进行测试分类的时候,不可能分错 5 个以上的样本。换句话说,如果测试发现这个学习器分错了 5 个以上的样本,那么这个学习器的泛化错误率就不可能是 0.3 。这时的泛化错误率应该是一个比 0.3 更大的数,因为泛化错误率比 0.3 小的学习器,分错 5 个以上样本的概率更低,所以泛化错误率小于 0.3 的学习器也不可能分错 5 个以上的样本。综合来说就是,泛化错误率小于等于 0.3 的学习器都不可能分错 5 个以上的样本。
这个学习器分错 5 个以上的样本是小概率事件,分错 6 个、 7 个以上样本更是小概率事件。但这里面的最小值 5 比较关键,通过将分错样本个数与 5 进行比较,我们就能决定是否拒绝“学习器泛化错误率是 0.3 ”这件事:如果分错样本个数小于等于 5 ,我们就不拒绝它,学习器的泛化错误率还有可能是 0.3 ;如果大于 5 ,我们就拒绝它,学习器的泛化错误率肯定不是 0.3 了。 6 、7 等等没法帮我们做这样的判断。
分错 5 个样本对应的测试错误率是 0.5 ,这个 0.5 就是临界值, 5% 是显著度,前面的结论可以描述为:在 5% 的显著度下,如果学习器的测试错误率小于等于 0.5 ,我们就不拒绝认为学习器的泛化错误率小于等于 0.3 ;如果学习器的测试错误率大于 0.5 ,我们就拒绝承认学习器的泛化错误率小于等于 0.3 ,或者说,学习器的泛化错误率要大于 0.3 。
现在我们按照书中的设定,用 ϵ 0 \epsilon_{0} ϵ0、 ϵ \epsilon ϵ、 ϵ ^ \hat{\epsilon} ϵ^、 ϵ ‾ \overline{\epsilon} ϵ、 α \alpha α 分别代替泛化错误率假设值 0.3、泛化错误率、测试错误率、错误率临界值以及显著度 5% ,对 “ ϵ ⩽ ϵ 0 \epsilon \leqslant \epsilon_{0} ϵ⩽ϵ0” 进行分析。假设在 α \alpha α 显著度下,使 ϵ ⩽ ϵ 0 \epsilon \leqslant \epsilon_{0} ϵ⩽ϵ0 成立的临界值 ϵ ‾ \overline{\epsilon} ϵ 已知,那么在学习器的泛化错误率的值等于 ϵ 0 \epsilon_{0} ϵ0 的情况下,学习器分错 ϵ ‾ × m \overline{\epsilon}\times m ϵ×m 个以上样例的概率和应该小于 α \alpha α ,用公式表示就是
∑ i = ϵ ‾ × m + 1 m ( m i ) ϵ 0 i ( 1 − ϵ 0 ) m − i < α \sum_{i=\overline{\epsilon} \times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) {\epsilon_{0}}^{i}(1-{\epsilon_{0}})^{m-i}<\alpha i=ϵ×m+1∑m(mi)ϵ0i(1−ϵ0)m−i<α
显然, ϵ ‾ \overline{\epsilon} ϵ 是以 ϵ \epsilon ϵ 为未知数的不等式
∑ i = ϵ × m + 1 m ( m i ) ϵ 0 i ( 1 − ϵ 0 ) m − i < α \sum_{i=\epsilon \times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) {\epsilon_{0}}^{i}(1-{\epsilon_{0}})^{m-i}<\alpha i=ϵ×m+1∑m(mi)ϵ0i(1−ϵ0)m−i<α
的解集中的最小值,也即
ϵ ‾ = min ϵ s.t. ∑ i = ϵ × m + 1 m ( m i ) ϵ 0 i ( 1 − ϵ 0 ) m − i < α (2.27*) \overline{\epsilon}=\min \epsilon \text { s.t. } \sum_{i=\epsilon \times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) {\epsilon_{0}}^{i}(1-{\epsilon_{0}})^{m-i}<\alpha\tag{2.27*} ϵ=minϵ s.t. i=ϵ×m+1∑m(mi)ϵ0i(1−ϵ0)m−i<α(2.27*)
这是我认为周老师想表达的式(2.27)意思,与原书公式有所不同。这里附上原式,如果我理解有误,欢迎大家指正。
ϵ ‾ = min ϵ s.t. ∑ i = ϵ 0 × m + 1 m ( m i ) ϵ i ( 1 − ϵ ) m − i < α (2.27) \overline{\epsilon}=\min \epsilon \text { s.t. } \sum_{i=\epsilon_{0} \times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) \epsilon^{i}(1-\epsilon)^{m-i}<\alpha\tag{2.27} ϵ=minϵ s.t. i=ϵ0×m+1∑m(mi)ϵi(1−ϵ)m−i<α(2.27)
上面的 α \alpha α 是“显著度”,对应图2.6的阴影部分的范围, 1 − α 1-\alpha 1−α 反映了结论的“置信度”,对应图2.6中非阴影部分的范围。假设检验的原假设是 “ ϵ ⩽ ϵ 0 \epsilon \leqslant \epsilon_{0} ϵ⩽ϵ0” ,最终求得的拒绝域是 ( ϵ ‾ , 1 ] (\overline{\epsilon},1] (ϵ,1]。此时,若测试错误率 ϵ ^ \hat{\epsilon} ϵ^ 小于等于临界值 ϵ ‾ \overline{\epsilon} ϵ ,则在 α \alpha α 的显著度下,假设“ ϵ ⩽ ϵ 0 \epsilon \leqslant \epsilon_{0} ϵ⩽ϵ0”不能被拒绝,即能以 1 − α 1-\alpha 1−α 的置信度认为,学习器的泛化错误率不大于 ϵ 0 \epsilon_{0} ϵ0 ;否则该假设可被拒绝,即在 α \alpha α 的显著度下可认为学习器的泛化错误率大于 ϵ 0 \epsilon_{0} ϵ0 。
当通过多次重复留出法或是交叉验证法等进行多次训练/测试时,我们会得到多个测试错误率,这时可使用“ t t t 检验”( t t t-test)。假定我们得到了 k k k 个测试错误率, ϵ ^ 1 , ϵ ^ 2 , … , ϵ ^ k \hat{\epsilon}_{1}, \hat{\epsilon}_{2}, \ldots, \hat{\epsilon}_{k} ϵ^1,ϵ^2,…,ϵ^k ,则平均测试错误率 μ \mu μ 和样本方差 S 2 S^{2} S2 (原书这里写的是“方差 σ 2 \sigma^{2} σ2 ”,看公式实际上是“样本方差”,为了与总体方差区分,我将描述改为了“样本方差 S 2 S^{2} S2 ”)为
μ = 1 k ∑ i = 1 k ϵ ^ i (2.28) \mu=\frac{1}{k} \sum_{i=1}^{k} \hat{\epsilon}_{i}\tag{2.28} μ=k1i=1∑kϵ^i(2.28)
S 2 = 1 k − 1 ∑ i = 1 k ( ϵ ^ i − μ ) 2 (2.29) S^{2}=\frac{1}{k-1} \sum_{i=1}^{k}\left(\hat{\epsilon}_{i}-\mu\right)^{2}\tag{2.29} S2=k−11i=1∑k(ϵ^i−μ)2(2.29)
这 k k k 个测试错误率可看作泛化错误率 ϵ 0 \epsilon_0 ϵ0 的独立采样,则变量
τ t = k ( μ − ϵ 0 ) S (2.30) \tau_{t}=\frac{\sqrt{k}\left(\mu-\epsilon_{0}\right)}{S}\tag{2.30} τt=Sk(μ−ϵ0)(2.30)
服从自由度为 k − 1 k-1 k−1 的 t t t 分布,如图2.7所示
对假设“ μ = ϵ 0 \mu=\epsilon_0 μ=ϵ0”和显著度 α \alpha α ,可计算出当测试错误率均值为 ϵ 0 \epsilon_0 ϵ0 时,在 1 − α 1-\alpha 1−α 概率内能观测到的最大错误率,即临界值。这里考虑双边(two-tailed)假设,如图2.7所示,两边阴影部分各有 a / 2 a/2 a/2 的面积。假定阴影部分范围分别为 [ − ∞ , t − α / 2 ] \left[-\infty, t_{-\alpha / 2}\right] [−∞,t−α/2] 和 [ t α / 2 , ∞ ] \left[t_{\alpha / 2}, \infty\right] [tα/2,∞] 。若 τ t \tau_{t} τt 位于临界值范围 ( t − α / 2 , t α / 2 ) \left(t_{-\alpha / 2}, t_{\alpha / 2}\right) (t−α/2,tα/2) 内,则不能拒绝假设“ μ = ϵ 0 \mu=\epsilon_0 μ=ϵ0”,即可认为泛化错误率为 ϵ 0 \epsilon_0 ϵ0 ,置信度为 1 − α 1-\alpha 1−α ;否则可拒绝该假设,即在该显著度下可认为泛化错误率与 ϵ 0 \epsilon_0 ϵ0 有显著不同。 α \alpha α 常用取值有 0.05 和 0.1 。表2.3给出了一些常用临界值。
上面介绍的两种方法是对关于单个学习器泛化性能的假设进行检验,下面将介绍对不同学习器的性能进行比较的假设检验方法。
2.4.2 交叉验证 t 检验
对两个学习器 A 和 B ,若我们使用 k k k 折交叉验证法得到的测试错误率分别为 ϵ 1 A , ϵ 2 A , … , ϵ k A \epsilon_{1}^{A}, \epsilon_{2}^{A}, \ldots, \epsilon_{k}^{A} ϵ1A,ϵ2A,…,ϵkA 和 ϵ 1 B , ϵ 2 B , … , ϵ k B \epsilon_{1}^{B}, \epsilon_{2}^{B}, \ldots, \epsilon_{k}^{B} ϵ1B,ϵ2B,…,ϵkB ,其中 ϵ i A \epsilon_{i}^{A} ϵiA 和 ϵ i B \epsilon_{i}^{B} ϵiB 是在相同的第 i i i 折训练/测试集上得到的结果,则可用 k k k 折交叉验证“成对 t t t 检验”(paired t t t-test)来进行比较检验。若两个学习器的性能相同,则它们使用相同的训练/测试集得到的测试错误率应该相同,即 ϵ i A = ϵ i B \epsilon_{i}^{A}=\epsilon_{i}^{B} ϵiA=ϵiB 。
具体来说,对 k k k 折交叉验证产生的 k k k 对测试错误率:先对每对结果求差, Δ i = ϵ i A − ϵ i B \Delta_{i}=\epsilon_{i}^{A}-\epsilon_{i}^{B} Δi=ϵiA−ϵiB ,若两个学习器性能相同,则差值均值应为零。因此,可根据差值 Δ 1 , Δ 2 , … , Δ k \Delta_{1}, \Delta_{2}, \dots, \Delta_{k} Δ1,Δ2,…,Δk 来对“学习器 A 与 B 性能相同”这个假设做 t t t 检验,计算出差值的均值 μ \mu μ 和样本方差 S 2 S^2 S2 (原书这里也是“方差 σ 2 \sigma^{2} σ2 ”),在显著度 α \alpha α 下,若变量
τ t = ∣ k μ S ∣ (2.31) \tau_{t}=\left|\frac{\sqrt{k} \mu}{S}\right|\tag{2.31} τt=∣∣∣∣∣Skμ∣∣∣∣∣(2.31)
小于临界值 t α / 2 , k − 1 t_{\alpha / 2, k-1} tα/2,k−1 ,则假设不能被拒绝,即认为两个学习器的性能没有显著差别;否则可认为两个学习器的性能有显著差别,且平均错误率较小的那个学习器性能较优。这里 t α / 2 , k − 1 t_{\alpha / 2, k-1} tα/2,k−1 是自由度为 k − 1 k-1 k−1 的 t t t 分布上尾部累积分布为 α / 2 \alpha/2 α/2 的临界值。
欲进行有效的假设检验,一个重要前提是测试错误率均为泛化错误率的独立采样。然而,通常情况下由于样本有限,在使用交叉验证等实验估计方法时,不同轮次的训练集会有一定程度的重叠,这就使得测试错误率实际上并不独立,会导致过高估计假设成立的概率。为缓解这一问题,可采用“ 5 × 2 交叉验证”法。
5 × 2 交叉验证是做 5 次 2 折交叉验证,在每次 2 折交叉验证之前随机将数据打乱,使得 5 次交叉验证中的数据划分不重复。对两个学习器 A 和 B ,第 i i i 次 2 折交叉验证将产生两对测试错误率,我们对它们分别求差,得到第 1 折上的差值 Δ i 1 \Delta^{1}_{i} Δi1 和第 2 折上的差值 Δ i 2 \Delta^{2}_{i} Δi2 。为缓解测试错误率的非独立性,我们仅计算第 1 次 2 折交叉验证的两个结果的平均值 μ = 0.5 ( Δ 1 1 + Δ 1 2 ) \mu=0.5\left(\Delta_{1}^{1}+\Delta_{1}^{2}\right) μ=0.5(Δ11+Δ12) ,但对每次 2 折实验的结果都计算出其样本方差 S i 2 = ( Δ i 1 − Δ i 1 + Δ i 2 2 ) 2 + ( Δ i 2 − Δ i 1 + Δ i 2 2 ) 2 S_{i}^{2}=\left(\Delta_{i}^{1}-\frac{\Delta_{i}^{1}+\Delta_{i}^{2}}{2}\right)^{2}+\left(\Delta_{i}^{2}-\frac{\Delta_{i}^{1}+\Delta_{i}^{2}}{2}\right)^{2} Si2=(Δi1−2Δi1+Δi2)2+(Δi2−2Δi1+Δi2)2 变量(原书这里用的是“方差 σ i 2 \sigma_{i}^{2} σi2 ”)
τ t = 5 μ ∑ i = 1 5 S i 2 = μ 0.2 ∑ i = 1 5 S i 2 (2.32) \tau_{t}=\frac{{\sqrt{5}}{\mu}}{\sqrt{\sum_{i=1}^{5} S_{i}^{2}}}=\frac{\mu}{\sqrt{0.2 \sum_{i=1}^{5} S_{i}^{2}}}\tag{2.32} τt=∑i=15Si25μ=0.2∑i=15Si2μ(2.32)
服从自由度为 5 的 t t t 分布,其双边检验的临界值 t α / 2 , 5 t_{\alpha / 2,5} tα/2,5 当 α = 0.05 \alpha=0.05 α=0.05 时为 2.5706 , α = 0.1 \alpha=0.1 α=0.1 时为 2.0150 。
2.4.3 McNemar检验
对二分类问题,使用留出法不仅可估计出学习器 A 和 B 的测试错误率,还可获得两学习器分类结果的差别,即两者都正确、都错误、一个正确另一个错误的样本数,如“列联表”(contingency table)2.4所示。
若我们做的假设是两学习器性能相同,则应有 e 01 = e 10 e_{01}=e_{10} e01=e10 。由于 e 01 + e 10 e_{01}+e_{10} e01+e10 通常很小,由带连续性校正的 McNemar 检验公式(这里的解释与原书有所不同),有变量
τ χ 2 = ( ∣ e 01 − e 10 ∣ − 1 ) 2 e 01 + e 10 (2.33) \tau_{\chi^{2}}=\frac{\left(\left|e_{01}-e_{10}\right|-1\right)^{2}}{e_{01}+e_{10}}\tag{2.33} τχ2=e01+e10(∣e01−e10∣−1)2(2.33)
服从自由度为 1 的 χ 2 \chi^{2} χ2 分布,即标准正态分布变量的平方。给定显著度 α \alpha α ,当以上变量值小于临界值 χ α 2 \chi_{\alpha}^{2} χα2 时,不能拒绝假设,即认为两学习器的性能没有显著差别;否则拒绝假设,即认为两者性能有显著差别,且平均错误率较小的那个学习器性能较优。自由度为 1 的 χ 2 \chi^{2} χ2 检验的临界值当 α = 0.05 \alpha=0.05 α=0.05 时为 3.8415 , α = 0.1 \alpha=0.1 α=0.1 时为 2.7055 。
2.4.4 Friedman 检验与 Nemenyi 后续检验
交叉验证 t t t 检验和 McNemar 检验都是在一个数据集上比较两个算法的性能,而在很多时候,我们会在一组数据集上对多个算法进行比较。这时,可以在每个数据集上分别列出两两比较的结果,在两两比较时使用前述方法;也可以用一种更为直接的方法,使用基于算法排序的 Friedman 检验。
假定我们用 D 1 D_1 D1、 D 2 D_2 D2、 D 3 D_3 D3 和 D 4 D_4 D4 四个数据集对算法 A A A、 B B B、 C C C 进行比较。首先,使用留出法或交叉验证法得到每个算法在每个数据集上的测试结果,然后在每个数据集上根据测试性能由好到坏排序,并赋予序值 1,2,…,若算法的测试性能相同,则平分序值。例如,在 D 1 D_1 D1 上,A 最好、B 其次、C 最差,在 D 2 D_2 D2 上,A 最好、B 与 C 性能相同,在 D 3 D_3 D3 上,A 最好、B 其次、C 最差,……,则可列出表 2.5,其中最后一行通过对每一列的序值求平均,得到平均序值。
然后,使用 Friedman 检验来判断这些算法性能是否都相同,若相同,则它们的平均序值应当相同。假定我们在 N N N 个数据集上比较 k k k 个算法,令 r i r_i ri 表示第 i i i 个算法的平均序值,为简化讨论,暂不考虑平分序值的情况,则 r i r_i ri 服从正态分布,其均值和方差分别为 ( k + 1 ) / 2 (k+1)/2 (k+1)/2 和 ( k 2 − 1 ) / 12 N (k^2-1)/12N (k2−1)/12N 。变量
τ χ 2 = k − 1 k ⋅ 12 N k 2 − 1 ∑ i = 1 k ( r i − k + 1 2 ) 2 = 12 N k ( k + 1 ) ( ∑ i = 1 k r i 2 − k ( k + 1 ) 2 4 ) (2.34) \begin{aligned} \tau_{\chi^{2}} &=\frac{k-1}{k} \cdot \frac{12 N}{k^{2}-1} \sum_{i=1}^{k}\left(r_{i}-\frac{k+1}{2}\right)^{2} \\ &=\frac{12 N}{k(k+1)}\left(\sum_{i=1}^{k} r_{i}^{2}-\frac{k(k+1)^{2}}{4}\right) \end{aligned}\tag{2.34} τχ2=kk−1⋅k2−112Ni=1∑k(ri−2k+1)2=k(k+1)12N(i=1∑kri2−4k(k+1)2)(2.34)
在 k k k 和 N N N 都较大时,服从自由度为 k − 1 k-1 k−1 的 χ 2 \chi^{2} χ2 分布。
这里对刚刚提到的均值和方差做一下简单的推导和说明,假设算法 i i i 在数据集 j j j 上的序值为 R j i R_{ji} Rji,则
E ( r i ) = ∑ i = 1 k r i k = ∑ i = 1 k ( ∑ j = 1 N R j i N ) k = ∑ i = 1 k ( ∑ j = 1 N R j i ) k N = N ∑ i = 1 k i k N = N k ( k + 1 ) 2 k N = k + 1 2 \begin{aligned} E(r_i) &=\frac{\sum_{i=1}^{k}r_i}{k} \\ &=\frac{\sum_{i=1}^{k}\left(\frac{\sum_{j=1}^{N}R_{ji}}{N}\right)}{k} \\ &=\frac{\sum_{i=1}^{k}\left(\sum_{j=1}^{N}R_{ji}\right)}{kN} \\ &=\frac{N\sum_{i=1}^{k}i}{kN} \\ &=\frac{N\frac{k(k+1)}{2}}{kN} \\ &=\frac{k+1}{2} \end{aligned} E(ri)=k∑i=1kri=k∑i=1k(N∑j=1NRji)=kN∑i=1k(∑j=1NRji)=kNN∑i=1ki=kNN2k(k+1)=2k+1
D ( r i ) = D ( ∑ j = 1 N R j i N ) = 1 N 2 ∑ j = 1 N D ( R j i ) = 1 N 2 N ( 1 N k ∑ j = 1 N ( ∑ i = 1 k ( R j i − k + 1 2 ) 2 ) ) = 1 N 2 k ∑ j = 1 N ( ∑ i = 1 k ( R j i 2 + ( k + 1 ) 2 4 − R j i ( k + 1 ) ) ) = 1 N 2 k ( N ∑ i = 1 k i 2 + N k ( k + 1 ) 2 4 − N ( k + 1 ) ∑ i = 1 k i ) = 1 N k ( k ( k + 1 ) ( 2 k + 1 ) 6 + k ( k + 1 ) 2 4 − k ( k + 1 ) 2 2 ) = k 2 − 1 12 N \begin{aligned} D(r_i) &=D(\frac{\sum_{j=1}^{N}R_{ji}}{N}) \\ &=\frac{1}{N^2}\sum_{j=1}^{N}D(R_{ji}) \\ &=\frac{1}{N^2}N(\frac{1}{Nk}\sum_{j=1}^{N}(\sum_{i=1}^{k}(R_{ji}-\frac{k+1}{2})^2)) \\ &=\frac{1}{N^2k}\sum_{j=1}^{N}(\sum_{i=1}^{k}(R_{ji}^2+\frac{(k+1)^2}{4}-R_{ji}(k+1))) \\ &=\frac{1}{N^2k}(N\sum_{i=1}^{k}i^2+\frac{Nk(k+1)^2}{4}-N(k+1)\sum_{i=1}^{k}i) \\ &=\frac{1}{Nk}(\frac{k(k+1)(2k+1)}{6}+\frac{k(k+1)^2}{4}-\frac{k(k+1)^2}{2}) \\ &=\frac{k^2-1}{12N} \end{aligned} D(ri)=D(N∑j=1NRji)=N21j=1∑ND(Rji)=N21N(Nk1j=1∑N(i=1∑k(Rji−2k+1)2))=N2k1j=1∑N(i=1∑k(Rji2+4(k+1)2−Rji(k+1)))=N2k1(Ni=1∑ki2+4Nk(k+1)2−N(k+1)i=1∑ki)=Nk1(6k(k+1)(2k+1)+4k(k+1)2−2k(k+1)2)=12Nk2−1
因为是排序, R j i R_{ji} Rji 一定是 1 1 1 到 k k k 按某种顺序的排列,所以 ∑ i = 1 k R j i = ∑ i = 1 k i \sum_{i=1}^{k}R_{ji}=\sum_{i=1}^{k}i ∑i=1kRji=∑i=1ki, ∑ i = 1 k R j i 2 = ∑ i = 1 k i 2 \sum_{i=1}^{k}R_{ji}^2=\sum_{i=1}^{k}i^2 ∑i=1kRji2=∑i=1ki2。
然而,上述这样的“原始 Friedman 检验”过于保守,现在通常使用变量
τ F = ( N − 1 ) τ χ 2 N ( k − 1 ) − τ χ 2 (2.35) \tau_{F}=\frac{(N-1) \tau_{\chi^{2}}}{N(k-1)-\tau_{\chi^{2}}}\tag{2.35} τF=N(k−1)−τχ2(N−1)τχ2(2.35)
其中 τ χ 2 \tau_{\chi^{2}} τχ2 由式(2.34)得到。 τ F \tau_{F} τF 服从自由度为 k − 1 k-1 k−1 和 ( k − 1 ) ( N − 1 ) (k-1)(N-1) (k−1)(N−1) 的 F F F 分布。表2.6给出了一些常用临界值。
若“所有算法的性能相同”这个假设被拒绝,则说明算法的性能显著不同,这时需要进行“后续检验”(post-hoc test)进一步区分各算法。常用的有 Nemenyi 后续检验。
Nemenyi 检验计算出平均序值差别的临界值域
C D = q α k ( k + 1 ) 6 N (2.36) C D=q_{\alpha} \sqrt{\frac{k(k+1)}{6 N}}\tag{2.36} CD=qα6Nk(k+1)(2.36)
表2.7给出了 α = 0.05 \alpha=0.05 α=0.05 和 0.1 0.1 0.1 时常用的 q α q_{\alpha} qα 值。若两个算法的平均序值之差超出了临界值域 C D CD CD ,则以相应的置信度拒绝“两个算法性能相同”这一假设。
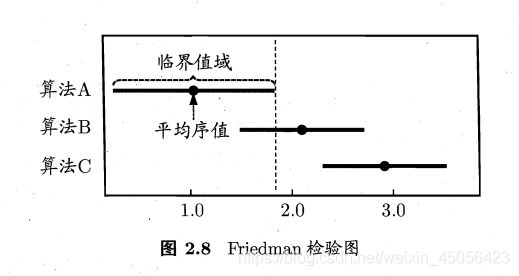
以表2.5中的数据为例,先根据式(2.34)和(2.35)计算出 τ F = 24.429 \tau_{F}=24.429 τF=24.429 ,由表2.6可知,它大于 α = 0.05 \alpha=0.05 α=0.05 时的 F F F 检验临界值 5.143 5.143 5.143 ,因此拒绝“所有算法性能相同”这个假设。然后使用 Nemenyi 后续检验,在表2.7中找到 k = 3 k=3 k=3 时 q 0.05 = 2.344 q_{0.05}=2.344 q0.05=2.344 ,根据式(2.36)计算出临界值域 C D = 1.657 CD=1.657 CD=1.657 ,由表2.5中的平均序值可知,算法 A 与 B 的差距,以及算法 B 与 C 的差距均未超过临界值域,而算法 A 与 C 的差距超过了临界值域,因此检验结果认为算法 A 与 C 的性能显著不同,而算法 A 与 B、以及算法 B 与 C 的性能没有显著差别。
上述检验比较可以直观地用 Friedman 检验图显示。例如,根据表2.5的序值结果可绘制出图2.8,图中纵轴显示各个算法,横轴是平均序值。对每个算法,用一个圆点显示其平均序值,以圆点为中心的横线段表示临界值域的大小。然后就可从图中观察,若两个算法的横线段有交叠,则说明这两个算法没有显著差别,否则说明两个算法有显著差别。从图2.8容易看出,算法 A 与 B 没有显著差别,因为它们的横线段有交叠区域,而算法 A 显著优于算法 C,因为它们的横线段没有交叠区域。
2.5 偏差与方差
除了通过实验估计泛化性能,人们往往还希望了解学习算法“为什么”具有这样的性能。“偏差-方差分解”(bias-variance decomposition)是解释学习算法泛化性能的一种重要工具。
偏差-方差分解试图对学习算法的期望泛化错误率进行拆解。我们知道,算法在不同训练集上学得的结果很可能不同,即便这些训练集是来自同一个分布。对测试样本 x \boldsymbol{x} x ,令 y D y_D yD 为 x \boldsymbol{x} x 在数据集中的标记, y y y 为 x \boldsymbol{x} x 的真实标记, f ( x ; D ) f(\boldsymbol{x} ; D) f(x;D) 为训练集 D D D 上学得模型 f f f 在 x \boldsymbol{x} x 上的预测输出。以回归任务为例,学习算法的期望预测为
f ˉ ( x ) = E D [ f ( x ; D ) ] (2.37) \bar{f}(\boldsymbol{x})=\mathbb{E}_{D}[f(\boldsymbol{x} ; D)]\tag{2.37} fˉ(x)=ED[f(x;D)](2.37)
使用样本数相同的不同训练集产生的方差为
var ( x ) = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] (2.38) \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]\tag{2.38} var(x)=ED[(f(x;D)−fˉ(x))2](2.38)
噪声为
ε 2 = E D [ ( y D − y ) 2 ] (2.39) \varepsilon^{2}=\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right]\tag{2.39} ε2=ED[(yD−y)2](2.39)
期望输出与真实标记的差别称为偏差(bias),即
bias 2 ( x ) = ( f ˉ ( x ) − y ) 2 (2.40) \operatorname{bias}^{2}(\boldsymbol{x})=(\bar{f}(\boldsymbol{x})-y)^{2}\tag{2.40} bias2(x)=(fˉ(x)−y)2(2.40)
为便于讨论,假定噪声期望为零,即 E D [ y D − y ] = 0 \mathbb{E}_{D}\left[y_{D}-y\right]=0 ED[yD−y]=0 。通过简单的多项式展开合并,可对算法的期望泛化误差进行分解:
E ( f ; D ) = E D [ ( f ( x ; D ) − y D ) 2 ] = E D [ ( f ( x ; D ) − f ˉ ( x ) + f ˉ ( x ) − y D ) 2 ] = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] + E D [ ( f ˉ ( x ) − y D ) 2 ] + E D [ 2 ( f ( x ; D ) − f ˉ ( x ) ) ( f ˉ ( x ) − y D ) ] = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] + E D [ ( f ˉ ( x ) − y D ) 2 ] = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] + E D [ ( f ˉ ( x ) − y + y − y D ) 2 ] = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] + E D [ ( f ˉ ( x ) − y ) 2 ] + E D [ ( y − y D ) 2 ] + 2 E D [ ( f ˉ ( x ) − y ) ( y − y D ) ] = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] + ( f ˉ ( x ) − y ) 2 + E D [ ( y D − y ) 2 ] (2.41) \begin{aligned} E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ &+\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\ =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\ =&\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right] \\ &+2 \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)\left(y-y_{D}\right)\right] \\ =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+(\bar{f}(\boldsymbol{x})-y)^{2}+\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right] \end{aligned}\tag{2.41} E(f;D)=======ED[(f(x;D)−yD)2]ED[(f(x;D)−fˉ(x)+fˉ(x)−yD)2]ED[(f(x;D)−fˉ(x))2]+ED[(fˉ(x)−yD)2]+ED[2(f(x;D)−fˉ(x))(fˉ(x)−yD)]ED[(f(x;D)−fˉ(x))2]+ED[(fˉ(x)−yD)2]ED[(f(x;D)−fˉ(x))2]+ED[(fˉ(x)−y+y−yD)2]ED[(f(x;D)−fˉ(x))2]+ED[(fˉ(x)−y)2]+ED[(y−yD)2]+2ED[(fˉ(x)−y)(y−yD)]ED[(f(x;D)−fˉ(x))2]+(fˉ(x)−y)2+ED[(yD−y)2](2.41)
于是,
E ( f ; D ) = bias 2 ( x ) + var ( x ) + ε 2 (2.42) E(f ; D)=\operatorname{bias}^{2}(x)+\operatorname{var}(x)+\varepsilon^{2}\tag{2.42} E(f;D)=bias2(x)+var(x)+ε2(2.42)
也就是说,泛化误差可分解为偏差、方差与噪声之和。
对式(2.41)的几点说明:
第三步到第四步
E D [ 2 ( f ( x ; D ) − f ˉ ( x ) ) ( f ˉ ( x ) − y D ) ] = 2 E D [ ( f ( x ; D ) − f ˉ ( x ) ) ⋅ f ˉ ( x ) ] − 2 E D [ ( f ( x ; D ) − f ˉ ( x ) ) ⋅ y D ] \begin{aligned} \mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] =& 2\mathbb{E}_{D}[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})) \cdot \bar{f}(\boldsymbol{x})]-2\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})) \cdot y_{D}\right] \end{aligned} ED[2(f(x;D)−fˉ(x))(fˉ(x)−yD)]=2ED[(f(x;D)−fˉ(x))⋅fˉ(x)]−2ED[(f(x;D)−fˉ(x))⋅yD]
f ˉ ( x ) \bar{f}(\boldsymbol{x}) fˉ(x) 是常数, f ( x ; D ) f(\boldsymbol{x} ; D) f(x;D) 和 y D y_{D} yD 相互独立,故
E D [ 2 ( f ( x ; D ) − f ˉ ( x ) ) ( f ˉ ( x ) − y D ) ] = 2 f ˉ ( x ) ⋅ [ E D [ f ( x ; D ) ] − f ˉ ( x ) ] − 2 E D [ y D ] ⋅ [ E D [ f ( x ; D ) ] − f ˉ ( x ) ] \begin{aligned} \mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] =& 2\bar{f}(\boldsymbol{x}) \cdot [\mathbb{E}_{D}[f(\boldsymbol{x} ; D)] - \bar{f}(\boldsymbol{x})]-2\mathbb{E}_{D}[y_{D}] \cdot [\mathbb{E}_{D}[f(\boldsymbol{x} ; D)] - \bar{f}(\boldsymbol{x})] \end{aligned} ED[2(f(x;D)−fˉ(x))(fˉ(x)−yD)]=2fˉ(x)⋅[ED[f(x;D)]−fˉ(x)]−2ED[yD]⋅[ED[f(x;D)]−fˉ(x)]
由式(2.37), E D [ f ( x ; D ) ] − f ˉ ( x ) = 0 \mathbb{E}_{D}[f(\boldsymbol{x} ; D)] - \bar{f}(\boldsymbol{x})=0 ED[f(x;D)]−fˉ(x)=0 ,故
E D [ 2 ( f ( x ; D ) − f ˉ ( x ) ) ( f ˉ ( x ) − y D ) ] = 0 \begin{aligned} \mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] = 0 \end{aligned} ED[2(f(x;D)−fˉ(x))(fˉ(x)−yD)]=0
第六步到第七步
f ˉ ( x ) \bar{f}(\boldsymbol{x}) fˉ(x) 、 y y y 是常数,故
E D [ ( f ˉ ( x ) − y ) 2 ] = ( f ˉ ( x ) − y ) 2 = bias 2 ( x ) \begin{aligned} \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)^{2}\right]=(\bar{f}(\boldsymbol{x})-y)^{2}=\operatorname{bias}^{2}(\boldsymbol{x}) \end{aligned} ED[(fˉ(x)−y)2]=(fˉ(x)−y)2=bias2(x)
假定噪声期望为零,即 E D [ y D − y ] = 0 \mathbb{E}_{D}\left[y_{D}-y\right]=0 ED[yD−y]=0 ,故
2 E D [ ( f ˉ ( x ) − y ) ( y − y D ) ] = 2 ( f ˉ ( x ) − y ) E D [ y − y D ] = 0 \begin{aligned} 2 \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)\left(y-y_{D}\right)\right]=2(\bar{f}(\boldsymbol{x})-y) \mathbb{E}_{D}\left[y-y_{D}\right]=0 \end{aligned} 2ED[(fˉ(x)−y)(y−yD)