SVM兵王问题详解
文章预览:
- (一) 识别系统的性能度量
-
- (1)几个重要的度量系统性能的标准
-
- (1)混淆矩阵(confusion matrix)
- (2)引入ROC曲线
-
- (2.1)通过ROC曲线获得系统性能度量
- (2.2)AUC指标
- (2.3)ERR
- (2.4)ROC曲线代码解析
(一) 识别系统的性能度量
- 上接纸面笔记记录:
- 不能仅用识别率来判断系统的性能。单纯用系统的识别率来判断系统的好坏,是没有意义的。例如,瞎猜的准确率为80%,那么你svm识别率为%95,那么还算高吗?
(1)几个重要的度量系统性能的标准
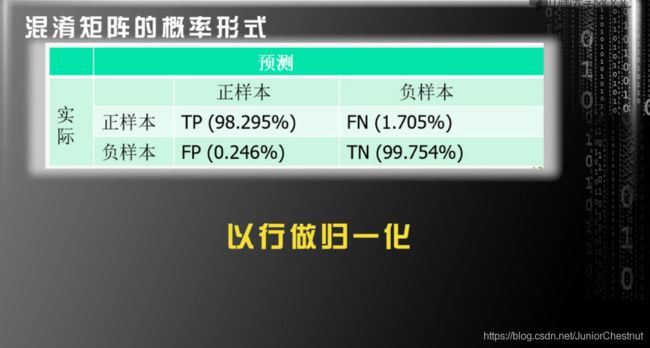
(1)混淆矩阵(confusion matrix)
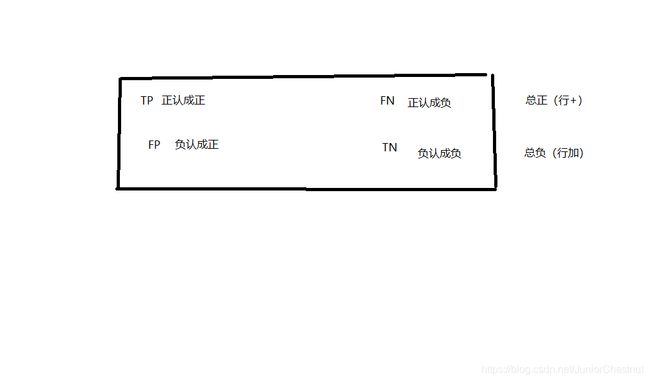
1.0 解释上图:
TP: T 代表正确true, TP代表读正样本(positive)正确;对了,把P读成P
TN: T代表正确true, N,negative,TN 代表读负样本正确;对了,把N读成N
FP:代表读正样本错误;错了,读成P(把谁读成P会错呢?)
FN:代表读负样本错误;错了,读成N
显然,正负样本的总数是固定的;那么可以概率化,归一化;
2.0 那么系统的识别率是多少呢?
识别成功个数:TP+TN; 总个数: TP+TN+FP+FN; 除一下就可以。99.61%
3.0 瞎猜的概率:由于负样本过多,所以全为负样本:TN + FP 89.96%
显然,这样的结果还可以,但是并不是非常好。
1.0 显然:TP+FN = 1; FP+TN = 1;
2.0 见下图:
(2)引入ROC曲线
1.0 解释ROC曲线:是以FP和TP为横终坐标画成;
2.0 对每个测试样本,计算上图公式:
3.0 然后 将得到的值从小到大开始排序;
4.0 把每一个值当作阈值,计算此时的TP和FP;连成一条曲线;
(2.1)通过ROC曲线获得系统性能度量

蓝色线最好,紫色线最差;因为在FP不变的情况下,TP越大越好。
(2.2)AUC指标
(2.3)ERR
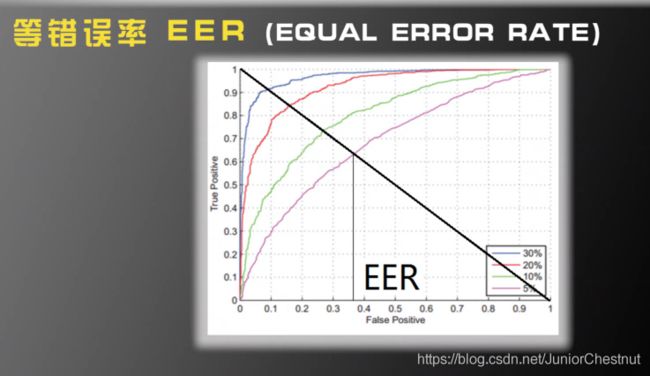
画一条45度线,EER为交点处的横坐标,显然,EER越小越好。
(2.4)ROC曲线代码解析
%Test the model on the remaining testing data and obtain the recognition rate.
clear all;
load model.mat;
load xTesting.mat;
load yTesting.mat;
% yPred 是对每个样本预测的标签; accuracy是在测试集上整体的识别率
% decisionValue: 是w^TX + b 的值;就是根据这个值贴标签
[yPred,accuracy,decisionValues] = svmpredict(yTesting,xTesting,model);
%draw ROC
[totalScores,index] = sort(decisionValues); % 先排序
labels = yTesting;
for i = 1:length(labels)
labels(i) = yTesting(index(i)); % 将decisionValue与标签值对应起来。
end;
truePositive = zeros(1,length(totalScores)+1);
trueNegative = zeros(1,length(totalScores)+1);
falsePositive = zeros(1,length(totalScores)+1);
falseNegative = zeros(1,length(totalScores)+1);
% 计算TP和FP的总的个数. 索引数一直为1;
for i = 1:length(totalScores)
if labels(i) == 1
truePositive(1) = truePositive(1)+1;
else
falsePositive(1) = falsePositive(1) +1;
end;
end;
% FP: 是如何得出来的: 原本是不能通过,认成了pass, label = -1;
% 由于排好序列了,那么,TP 和 FP的个数,其实是递减的。
for i = 1:length(totalScores)
if labels(i) == 1
truePositive(i+1) = truePositive(i)-1;
falsePositive(i+1) = falsePositive(i);
else
falsePositive(i+1) = falsePositive(i)-1;
truePositive(i+1) = truePositive(i);
end;
end;
% 概率化;
truePositive = truePositive/truePositive(1);
falsePositive = falsePositive/falsePositive(1);
plot(falsePositive, truePositive);
inc = 0.001;
startIndex = 1;
endIndex = length(falsePositive)
pointerIndex = 1;
pointerValue = falsePositive(1);
newFalsePositive = [];
newTruePositive = [];
while pointerIndex<=length(falsePositive)
while pointerIndex<=length(falsePositive) && falsePositive(pointerIndex)>falsePositive(startIndex)-inc
pointerIndex = pointerIndex +1;
end;
newFalsePositive = [newFalsePositive, falsePositive(startIndex)];
newTruePositive = [newTruePositive, mean(truePositive(startIndex:min(pointerIndex,length(truePositive))))];
startIndex = pointerIndex;
end;
plot(newFalsePositive, newTruePositive);
clear all;
% Read the data.
fid = fopen('krkopt.DATA');
c = fread(fid, 3);
vec = zeros(6,1);
xapp = []; % 接收六维的数据,先声明
yapp = []; % 接收所有的标签,先声明
while ~feof(fid)
string = [];
c = fread(fid,1);
flag = flag+1;
while c~=13 % 13代表回车; // 这里是读一行
string = [string, c];
c=fread(fid,1);
end;
fread(fid,1); % 这里是处理一行
if length(string)>10
vec(1) = string(1) - 96; % 把a变为整数1;
vec(2) = string(3) - 48;
vec(3) = string(5) - 96;
vec(4) = string(7) - 48;
vec(5) = string(9) - 96;
vec(6) = string(11) - 48;
xapp = [xapp,vec];
if string(13) == 100 % 13是因为第13个是draw(和棋)100是d;
yapp = [yapp,1];
else
yapp = [yapp,-1];
end;
end;
end;
fclose(fid);
[N,M] = size(xapp); % [N,M]是获取xapp的维度,例如3*4,N = 3,M = 4
p = randperm(M); % 直接打乱了训练样本,并且把列数作为行向量保存
% 1~M的整数随机置换
numberOfSamplesForTraining = 5000;
xTraining = [];
yTraining = [];
for i=1:numberOfSamplesForTraining
xTraining = [xTraining,xapp(:,p(i))]; % 这是从总样本中,取随机一列的全部元素
yTraining = [yTraining,yapp(p(i))]; % 这是取上面元素对应的标签
end;
xTraining = xTraining'; % 取转置
yTraining = yTraining';
xTesting = [];
yTesting = [];
for i=numberOfSamplesForTraining+1:M % 遍历剩下的数据作为测试数据
xTesting = [xTesting,xapp(:,p(i))]; % 注意同样用的p(i)
yTesting = [yTesting,yapp(p(i))];
end;
xTesting = xTesting'; % 取转置
yTesting = yTesting';
%%%%%%%%%%%%%%%%%%%%%%%%
%Normalization 归一化
[numVec,numDim] = size(xTraining);
avgX = mean(xTraining); % 这里是对每一列求平均值
stdX = std(xTraining); % 对每一列求方差
for i = 1:numVec % 以行遍历所有数据
xTraining(i,:) = (xTraining(i,:)-avgX)./stdX;
end;
[numVec,numDim] = size(xTesting);
for i = 1:numVec
xTesting(i,:) = (xTesting(i,:)-avgX)./stdX;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%SVM Gaussian kernel
%Search for the optimal C and gamma, K(x1,x2) = exp{-||x1-x2||^2/gamma} to
%make the recognition rate maximum.
%Firstly, search C and gamma in a crude scale (as recommended in 'A practical Guide to Support Vector Classification'))
CScale = [-5, -3, -1, 1, 3, 5,7,9,11,13,15];
gammaScale = [-15,-13,-11,-9,-7,-5,-3,-1,1,3];
C = 2.^CScale;
gamma = 2.^gammaScale;
maxRecognitionRate = 0;
for i = 1:length(C) % 找到最佳的超参数 c 和 gama 的下标
for j = 1:length(gamma) % svm训练参数设置:
cmd=['-t 2 -c ',num2str(C(i)),' -g ',num2str(gamma(j)),' -v 5'];
recognitionRate = svmtrain(yTraining,xTraining,cmd); %训练数据和参数
if recognitionRate>maxRecognitionRate
maxRecognitionRate = recognitionRate
maxCIndex = i;
maxGammaIndex = j;
end;
end;
end;
%Then search for optimal C and gamma in a refined scale.
n = 10; % 用最好的超参数,重新训练 %max 是返回最大的数
minCScale = 0.5*(CScale(max(1,maxCIndex-1))+CScale(maxCIndex));
maxCScale = 0.5*(CScale(min(length(CScale),maxCIndex+1))+CScale(maxCIndex));
newCScale = [minCScale:(maxCScale-minCScale)/n:maxCScale];
minGammaScale = 0.5*(gammaScale(max(1,maxGammaIndex-1))+gammaScale(maxGammaIndex));
maxGammaScale = 0.5*(gammaScale(min(length(gammaScale),maxGammaIndex+1))+gammaScale(maxGammaIndex));
newGammaScale = [minGammaScale:(maxGammaScale-minGammaScale)/n:maxGammaScale];
newC = 2.^newCScale;
newGamma = 2.^newGammaScale;
maxRecognitionRate = 0;
for i = 1:length(newC)
for j = 1:length(newGamma)
cmd=['-t 2 -c ',num2str(newC(i)),' -g ',num2str(newGamma(j)),' -v 5'];
recognitionRate = svmtrain(yTraining,xTraining,cmd);
if recognitionRate>maxRecognitionRate
maxRecognitionRate = recognitionRate
maxC = newC(i);
maxGamma = newGamma(j);
end;
end;
end;
%Train the SVM model by the optimal C and gamma.
cmd=['-t 2 -c ',num2str(maxC),' -g ',num2str(maxGamma)];
model = svmtrain(yTraining,xTraining,cmd);
save model.mat model;
save xTesting.mat xTesting;
save yTesting.mat yTesting;
% plot(falsePositive,truePositive);