Python吴恩达深度学习作业7 -- 深度神经网络的正则化
正则化
深度学习模型具有很高的灵活性和能力,如果训练数据集不够大,将会造成一个严重的问题–过拟合。尽管它在训练集上效果很好,但是学到的网络不能应用到测试集中!
你将学习:在深度学习模型中使用正则化。
# import packages
import numpy as np
import matplotlib.pyplot as plt
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
import sklearn
import sklearn.datasets
import scipy.io
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
问题陈述:你刚刚被法国足球公司聘为AI专家。他们希望你推测法国守门员将球踢出去的位置,以便法国队的求圆可以用头将球击中。
守门员将球踢到空中,每支球队的球员都在尽力用头击球
他们为你提供了法国过去10场比赛的二维数据集。
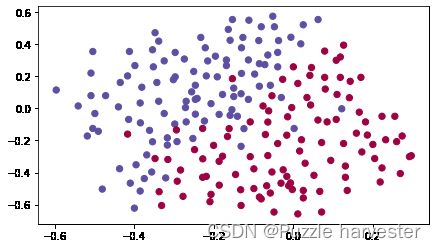
train_X, train_Y, test_X, test_Y = load_2D_dataset()
数据中每个点对应于足球场上的位置,在该位置上,法国守门员从足球场左侧射出球后,足球运动员用他/她的头部击中了球。
- 如果圆点为蓝色,则表示法国求圆设法用头部将球击中
- 如果圆点为红色,则表示另一支球队的球员用头撞球
你的目标:运用深度学习模型预测守门员应将球踢到球场上的位置。
数据集分析:该数据集含有噪音,但看起来一条将左上半部分(蓝色)于右下半部分(红色)分开的对角线会比较有效。
你将首先尝试非正则化模型。然后学习如何对其进行正则化,并决定选择那种模型来解决法国足球公司的问题。
1 非正则化模型
你将使用以下神经网络,可以如下使用此模型:
- 在regularization mode中,通过
lambd将输入设置为非零值。我们使用lambd代替lambda,因为lambda是Python中的保留关键字。 - 在dropout mode中,将
keep_prob设置为小于1的值
首先,你将尝试不进行任何正则化的模型。然后,你将实现:
- L2正则化函数:
compute_cost_with_regularization()和backward_propagation_with_regularization() - Dropout函数:
forward_propagation_with_dropout()和backward_propagation_with_dropout()
在每个部分中,你都将使用正确的输入来运行此模型,以便它调用已实现的函数。查看以下代码以熟悉该模型。
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)
learning_rate -- learning rate of the optimization
num_iterations -- number of iterations of the optimization loop
print_cost -- If True, print the cost every 10000 iterations
lambd -- regularization hyperparameter, scalar
keep_prob - probability of keeping a neuron active during drop-out, scalar.
Returns:
parameters -- parameters learned by the model. They can then be used to predict.
"""
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
让我们在不进行任何正则化的情况下训练模型,并观察训练/测试集的准确性。
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
Cost after iteration 0: 0.6557412523481002
Cost after iteration 10000: 0.16329987525724213
Cost after iteration 20000: 0.13851642423245572
On the training set:
Accuracy: 0.9478672985781991
On the test set:
Accuracy: 0.915
训练精度为94.8%,而测试精度为91.5%。这是基准模型的表现(你将观察到正则化对该模型的影响)。运行以下代码以绘制模型的决策边界。
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
非正则化模型显然过度拟合了训练集,拟合了一些噪声点!现在让我们看一下减少过拟合的两种手段。
2 L2正则化
避免过拟合的标准方法称为L2正则化,她将损失函数从:
J = − 1 m ∑ i = 1 m ( y ( i ) log ( a [ L ] ( i ) ) + ( 1 − y ( i ) ) log ( 1 − a [ L ] ( i ) ) ) (1) J = -\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} \tag{1} J=−m1i=1∑m(y(i)log(a[L](i))+(1−y(i))log(1−a[L](i)))(1)
修改到:
J r e g u l a r i z e d = − 1 m ∑ i = 1 m ( y ( i ) log ( a [ L ] ( i ) ) + ( 1 − y ( i ) ) log ( 1 − a [ L ] ( i ) ) ) ⏟ cross-entropy cost + 1 m λ 2 ∑ l ∑ k ∑ j W k , j [ l ] 2 ⏟ L2 regularization cost (2) J_{regularized} = \small \underbrace{-\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} }_\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W_{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{2} Jregularized=cross-entropy cost −m1i=1∑m(y(i)log(a[L](i))+(1−y(i))log(1−a[L](i)))+L2 regularization cost m12λl∑k∑j∑Wk,j[l]2(2)
让我们修改损失并观察结果。
练习:实现compute_cost_with_regularization(),以计算公式(2)的损失。要计算 ∑ k ∑ j W k , j [ l ] 2 \sum\limits_k\sum\limits_j W_{k,j}^{[l]2} k∑j∑Wk,j[l]2,请使用:
np.sum(np.square(Wl))
请注意,你必须对 W [ 1 ] W^{[1]} W[1], W [ 2 ] W^{[2]} W[2]和 W [ 3 ] W^{[3]} W[3]执行次操作,然后三个项相加并乘以 1 m λ 2 \frac {1}{m}\frac {\lambda}{2} m12λ。
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
用L2正则化实现代价函数。见上式(2)。
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y)
L2_regularization_cost = (1./m*lambd/2)*(np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
cost = cross_entropy_cost + L2_regularization_cost
return cost
A3, Y_assess, parameters = compute_cost_with_regularization_test_case()
print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1)))
cost = 1.7864859451590758
当然,因为你更改了损失,所以还需要更改反向传播!必须针对新损失函数计算所有梯度。
练习:实现正则化后的反向传播。更改仅涉及dW1,dW2和dW3。对于每一个,你必须添加正则化的梯度( d d W ( 1 2 λ m W 2 ) = λ m W \frac{d}{dW} ( \frac{1}{2}\frac{\lambda}{m} W^2) = \frac{\lambda}{m} W dWd(21mλW2)=mλW)。
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
参数:
X -- 输入数据集,形状(输入大小,示例数量)
Y -- “true”标签矢量,形状(输出大小,示例数)
cache -- 缓存forward_propagation()的输出
lambd -- 正规化hyperparameter,标量
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T) + lambd / m * W3
db3 = 1. / m * np.sum(dZ3, axis = 1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd = 0.7)
print ("dW1 = "+ str(grads["dW1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("dW3 = "+ str(grads["dW3"]))
dW1 = [[-0.25604646 0.12298827 -0.28297129]
[-0.17706303 0.34536094 -0.4410571 ]]
dW2 = [[ 0.79276486 0.85133918]
[-0.0957219 -0.01720463]
[-0.13100772 -0.03750433]]
dW3 = [[-1.77691347 -0.11832879 -0.09397446]]
现在让我们使用L2正则化( λ = 0.7 \lambda = 0.7 λ=0.7)运行的模型。model()函数将调用:
compute_cost_with_regularization代替compute_costbackward_propagation_with_regularization代替backward_propagation
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
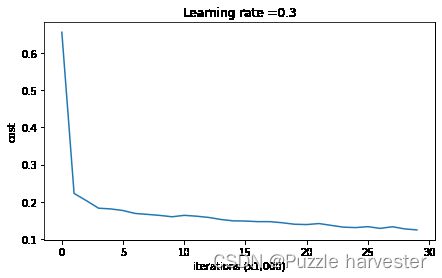
Cost after iteration 0: 0.6974484493131264
Cost after iteration 10000: 0.26849188732822393
Cost after iteration 20000: 0.2680916337127301
On the train set:
Accuracy: 0.9383886255924171
On the test set:
Accuracy: 0.93
Nice!测试集的准确性提高到93%。你成功拯救了法国足球队!
模型不再过拟合训练数据了。让我们绘制决策边界看一下。
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
观察:
- λ \lambda λ的值是你可以调整开发集的超参数。
- L2正则化使用决策边界更平滑。如果 λ \lambda λ太大,则也可能"过度平滑",从而使模型偏差较高。
L2正则化的原理:
L2正则化基于以下假设:权重较小的模型比权重较大的模型更简单。因此,通过对损失函数中权重的平方值进行惩罚,可以将所有权重驱动为较小的值。比重太大会使损失过高!这将导致模型更平滑,输出随着输入的变化而变化更慢。
你应该记住L2正则化的影响:
- 损失计算:
- 正则化条件会添加到损失函数中
- 反向传播函数:
- 有关权重矩阵的渐变在还有其他术语
- 权重最终变小(“权重衰减”):
- 权重被推到较小的值。
3 Dropout
最后,Dropout是广泛用于深度学习的正则化技术。
它会在每次迭代中随机关闭一些神经元。
要了解Dropout,可以思考与朋友进行以下对话:
- 朋友:“为什么你需要所有神经元来训练你的网络以分类图像?”。
- 你:“因为每个神经元都有权重,并且可以学习图像的特定特征/细节/形状。我拥有的神经元越多,模型学习的特征就越丰富!”
- 朋友:“我知道了,但是你确定你的神经元学习的是不同的特征而不是全部相同的特征吗?”
- 你:“这是个好问题……同一层中的神经元实际上并不关联。应该绝对有可能让他们学习相同的图像特征/形状/形式/细节...这是多余的。为此应该有一个解决方案。”
在每次迭代中,你以概率 1 − k e e p p r o b 1-keep_prob 1−keepprob或以概率 k e e p p r o b keep_prob keepprob(此处为50%)关闭此层的每个神经元。关闭的神经元对迭代的正向和反向传播均无助于训练。
1 s t 1^{st} 1st层:我们平均关闭了40%的神经元。 3 r d 3^{rd} 3rd层:我们平均关闭了20%的神经元。
当你关闭某些神经元时,实际上是在修改模型。Dropout背后的想法是,在每次迭代中,你将训练仅使用神经元子集的不同模型。通过Dropout,你的神经元对另一种特定神经元的激活变得不那么敏感,因为另一神经元可能随时关闭。
3.1 带有Dropout的正向传播
练习:实现带有Dropout的正向传播。你正在使用3层的神经网络,并将为第一和第二隐藏层添加Dropout。我们不会将Dropout应用于输入层或输出层。
说明:
-
在讲座中,我们讨论了使用
np.random.rand()创建于 a [ 1 ] a^{[1]} a[1]形状相同的变量 d [ 1 ] d^{[1]} d[1]的方法,一随机获取0到1之间的数。在这里,你将使用向量化的实现,创建一个与 A [ 1 ] A^{[1]} A[1]的矩阵维度相同的随机矩阵 D [ 1 ] = [ d [ 1 ] ( 1 ) d [ 1 ] ( 2 ) . . . d [ 1 ] ( m ) ] D^{[1]}=[d^{[1](1)}d^{[1](2)}...d^{[1](m)}] D[1]=[d[1](1)d[1](2)...d[1](m)]。 -
通过对 D [ 1 ] D^{[1]} D[1]中的值进行阈值设置,将 D [ 1 ] D^{[1]} D[1]的每个条目设置为0(概率为
1-keep_prob)或1(概率为keep_prob)。提示:将矩阵X的所有条目设置为0(如果概率小于0.5)或1(如果概率大于0.5),则可以执行:X = (X < 0.5)。注意0和1分别对应False和True。 -
将 A [ 1 ] A^{[1]} A[1]设置为 A [ 1 ] ∗ D [ 1 ] A^{[1]} * D^{[1]} A[1]∗D[1](关闭一些神经元)。你可以将 D [ 1 ] D^{[1]} D[1]视为掩码,这样当它与另一个矩阵相乘时,关闭某些值。
-
将 A [ 1 ] A^{[1]} A[1]除以
keep_prob。通过这样做,你可以确保损失结果仍具有与Dropout相同的期望值。(从技术也称为反向dropout)
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0],A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
X_assess, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob = 0.7)
print ("A3 = " + str(A3))
A3 = [[0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]]
3.2 带有dropout的反向传播
练习:实现带有的dropout的反向传播。和之前一样,训练一个3层的网络。使用存储在缓存中的掩码 D 1 D^{1} D1和 D 2 D^{2} D2,添加dropout到第一和第二个隐藏层。
说明:
-
你先前通过在A1上应用掩码 D [ 1 ] D^{[1]} D[1]来关闭正向传播过程中的某些神经元。在反向传播中,你将必须将相同的掩码 D [ 1 ] D^{[1]} D[1]重新应用于dA1来关闭相同的神经元。
-
在正向传播过程中,你已将A1除以keep_prob。因此,在反向传播中,必须再次将dA1除以keep_prob(计算的解释是,如果 A [ 1 ] A^{[1]} A[1]被keep_prob缩放,则其派生的 d A [ 1 ] dA^{[1]} dA[1]也由相同的keep_prob缩放)。
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis = 1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # Step 1:应用掩码D2关闭前向传播过程中的相同神经元
dA2 = dA2 / keep_prob # Step 2:测量未被关闭的神经元的价值
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis = 1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis = 1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob = 0.8)
print ("dA1 = " + str(gradients["dA1"]))
print ("dA2 = " + str(gradients["dA2"]))
dA1 = [[ 0.36544439 0. -0.00188233 0. -0.17408748]
[ 0.65515713 0. -0.00337459 0. -0. ]]
dA2 = [[ 0.58180856 0. -0.00299679 0. -0.27715731]
[ 0. 0.53159854 -0. 0.53159854 -0.34089673]
[ 0. 0. -0.00292733 0. -0. ]]
现在让我们使用dropout(keep_prob = 0.86)运行模型。 这意味着在每次迭代中,你都以24%的概率关闭第1层和第2层的每个神经元。 函数model()将调用:
forward_propagation_with_dropout而不是forward_propagation。backward_propagation_with_dropout,而不是backward_propagation。
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
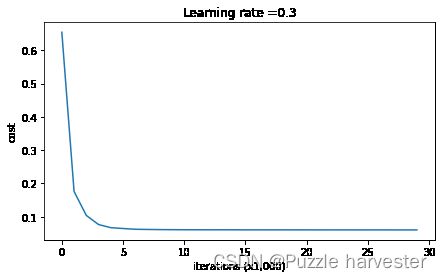
Cost after iteration 0: 0.6543912405149825
D:\VR\Virtual_Environment\Scripts\Deep_Learning\week7\reg_utils.py:236: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
D:\VR\Virtual_Environment\Scripts\Deep_Learning\week7\reg_utils.py:236: RuntimeWarning: invalid value encountered in multiply
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
Cost after iteration 10000: 0.0610169865749056
Cost after iteration 20000: 0.060582435798513114
On the train set:
Accuracy: 0.9289099526066351
On the test set:
Accuracy: 0.95
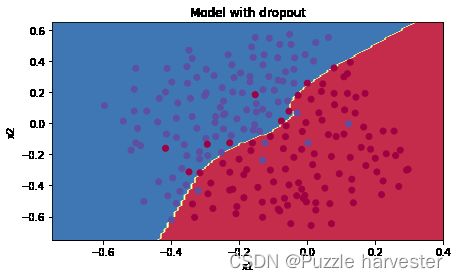
Dropout效果很好!测试精度再次提高(达到95%)!模型并未过拟合训练集,并且在测试集上表现很好。法国足球队将永远感激你!
运行以下代码以绘制决策边界。
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
*注意:
- 使用dropout时的常见错误是在训练和测试中都使用。你只能在训练中使用dropout(随机删除节点)。
- 深度学习框架,例如tensorflow, PaddlePaddle, keras或者 caffe 附带dropout层的实现。不需强调-相信你很快就会学习到其中的一些框架。
关dropout你应该记住的事情:
- dropout是一种正则化技术。
- 仅在训练期间使用dropout,在测试期间不要使用。
- 在正向和反向传播期间均应用dropout。
- 在训练期间,将每个dropout层除以keep_prob,以保持激活的期望值相同。例如,如果keep_prob为0.5,则平均而言,我们将关闭一半的节点,因此输出将按0.5缩放,因为只有剩余的一半对解决方案有所贡献。除以0.5等于乘以2,因此输出现在具有相同的期望值。你可以检查此方法是否有效,即使keep_prob的值不是0.5。
4 结论
这是我们三个模型的结果:
| 模型 | 训练精度 | 测试精度 |
| 三层神经网络,无正则化 | 95% | 91.50% |
| 具有L2正则化的3层NN | 94% | 93% |
| 具有dropout的3层NN | 93% | 95% |
请注意,正则化会损害训练集的性能! 这是因为它限制了网络过拟合训练集的能力。 但是,由于它最终可以提供更好的测试准确性,因此可以为你的系统提供帮助。
我们希望你从此笔记本中记住的内容:
- 正则化将帮助减少过拟合。
- 正则化将使权重降低到较低的值。
- L2正则化和Dropout是两种非常有效的正则化技术。