Two are Better than One: Joint Entity and Relation Extraction with Table-Sequence Encoders

Two are Better than One: Joint Entity and Relation Extraction with Table-Sequence Encoders

命名实体识别和关系提取是两个重要的基本问题。为了同时解决这两个任务，已经提出了联合学习算法，其中许多算法将联合任务作为一个填表问题。然而，他们通常专注于学习一个单一的编码器（通常是以表的形式学习表示）来捕捉同一空间内两个任务所需的信息。我们认为，在学习过程中设计两个不同的编码器来捕捉这两种不同类型的信息是有益的。在这项工作中，我们提出了新的表格-序列编码器，其中两个不同的编码器–一个表格编码器和一个序列编码器被设计为在表征学习过程中相互帮助。我们的实验证实了拥有两个编码器比一个编码器的优势。在几个标准数据集上，我们的模型显示出比现有的方法有明显的改进。

1.介绍

NER任务，即命名实体识别，命名实体就是以名称为标识的实体。简单来说，如果我们听到一个名字，就能知道这个东西是哪一个具体的事物，那么这个事物就是命名实体。命名实体识别（NER）就是要在文本中识别出命名实体。

RE任务，即关系抽取，关系抽取（Relation Extraction, RE）是自然语言处理的任务之一。该任务的定义是，给定标注了两个实体的句子，返回两个实体之间的语义关系。比如，给定句子“1993年2月15日，李彤出生在长春市。”，“李彤”和“长春市”返回关系“人-出生地”。

这两项任务都旨在从非结构化文本中提取结构化信息。大部分情况下，我们喜欢用三元组的数据结构来描述抽取到的信息。

• 三元组的表达能力非常丰富，几乎所有事情都可以自然或者强行的表达成三元组，比如随便一句”今天天气真冷“ 表达为 天气-状态-冷。

三元组千千万，我应该怎么抽？

当我们拿到一个信息抽取的任务，需要明确我们抽取的是什么，”今天天气真冷“，我们要抽的天气的状态天气-状态-冷，而非 今天-气候-冷(虽然也可以这样抽)，因此一般会首先定义好我们要抽取的数据结构模式schema, 会确定谓词以及主语并与的类型

一个三元组schema的例子，其中Subject_type代表主语类型，Predicate是谓词，Object_type指宾语类型：

Subject_type： 人物
Predicate:  出生地
Object_type: 地点

一种典型的方法是首先识别命名词实体，然后在每两个实体之间执行分类以提取关系，形成管道具体如下：

pipline两步走: 将关系抽取分解为NER任务和分类任务，NER任务标注主语或宾语，分类主要针对定义的schema中的有限个谓词进行分类。根据具体任务不同，有些可能是两步走或者三步走，pipline任务的顺序先分类还是先标注也会有差异

• Pipline优势：每一步分别针对各个任务进行，表征是task-specific， 相对来说精度较高
• Pipline缺陷：- 任务有顺序会存在误差传递问题，即在预测时下一步任务会受上一步误差影响，而在训练阶段没有这种误差，因此存在训练和预测阶段的gap - 分开的任务在一句话中多个实体关系时，比较难解决实体和关系的对应问题，以及重叠关系

还有一种现阶段比较新颖的方法是联合执行这两项任务

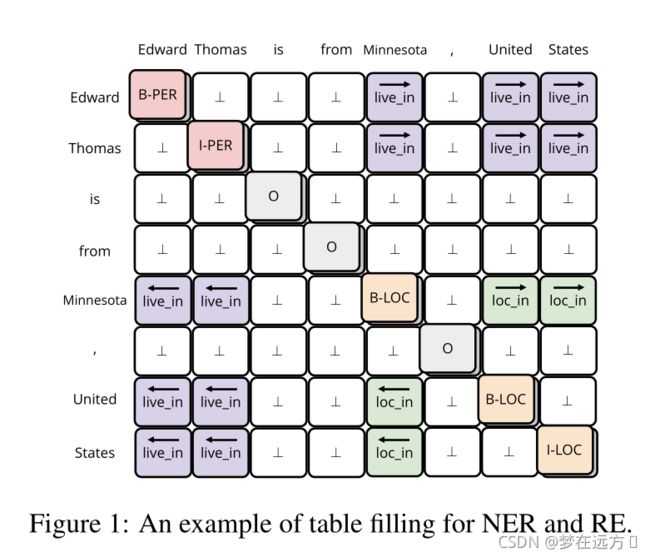
joint learning： joint learing可以理解为采用多任务的方式，同时进行NER和关系分类任务, 在众多joint learning中最出众的是采用table filled 方式，即任务的输出是filled一张有text-sequence构成的表，在表中的位置表达除了词与词的连接，该位置的标注则标出了谓语（如下图）

“B-X”：表示此元素所在的片段属于X类型并且此元素在此片段的开头。

“I-X”：表示此元素所在的片段属于X类型并且此元素在此片段的中间位置。

“O”：不属于任何类型。

• 优势：1. 两个任务的表征有交互作用可能辅助任务的学习2. 不用训练多个模型，一个模型解决问题，不存在训练与预测时的gap
• 缺陷：1. 两个任务的表征可能冲突，影响任务效果2. Fill table本质仍然是转成sequence来fill，未能充分利用table结构信息

作者点名了本文的三大点贡献

• 作者没有用单一的表示来预测实体和关系，而是专注于分别为NER和RE学习两种类型的表示，即序列表示和表表示。

  好处：一方面，这两种独立的表示可以用来捕获特定于任务的信息。另一方面，作者设计了一种机制，允许它们相互作用，以便利用NER和RE任务的内在联系。

• 作者使用了MD-RNN来更好的获取2D表的结构信息。

• 作者有效地利用了BERT注意力权重中携带的词-词交互信息，进一步提高了性能。

2.问题表示

对于NER任务，我们假设其为一个序列标记问题，${\mathbf{y}}^{\mathrm{N}\mathrm{E}\mathrm{R}}$使用我们上面提到的标准BIO Scheme

对于RE任务，我们输入一个句子$\mathbf{x}={\left[x_i\right]}_{1\le i\le N}$,构建一个tag_table ${\mathbf{y}}^{\mathrm{R}\mathrm{E}}={\left[y_{i,j}^{\mathrm{R}\mathrm{E}}\right]}_{1\le i,j\le N}$这个句子中$x_{i^b},\dots ,x_{i^e}$和$x_{j^b},\dots ,x_{j^e}$存在关系$r$,那么$y_{i,j}^{\mathrm{R}\mathrm{E}}=r$,$y_{j,i}^{\mathrm{R}\mathrm{E}}=r$,对于没有关系的地方使用$\perp$表示。

3.建模

3.1 Text Embedder

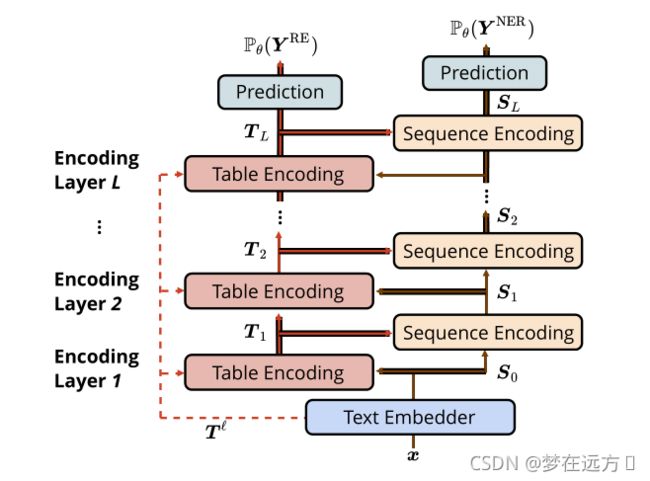
在Text Embedder部分，作者分别使用了LSTM进行了word Embedding ($x^w$)和 Character Embedding($x^c$)，同时，也是用Bert进行了Word Embedding($x^l$)来使得具有一种语境化的Word Embedding

$${\mathbf{S}}_0=\mathrm{Linear}\left(\left[{\mathbf{x}}^c;{\mathbf{x}}^w;{\mathbf{x}}^{\ell }\right]\right)$$

$${\mathbf{S}}_0\in {\mathbb{R}}^{N\times H}$$

N代表N个words，H代表隐藏层大小

最后将得到的三部分进行一个linear projection，将其结果作为Text Embedder的输出，也就是图中的$S_0$.

此外，作者在其代码实现中，在获得到Embedding前，首先先送入了一个dropout，然后在送入了一个线性层得到最后的$S_0$

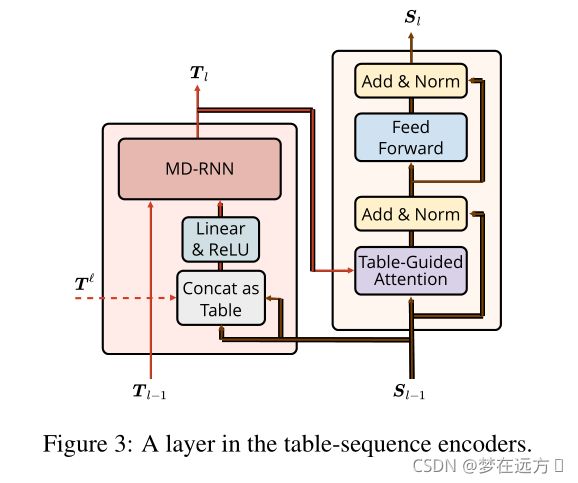
3.2 Table Encoder

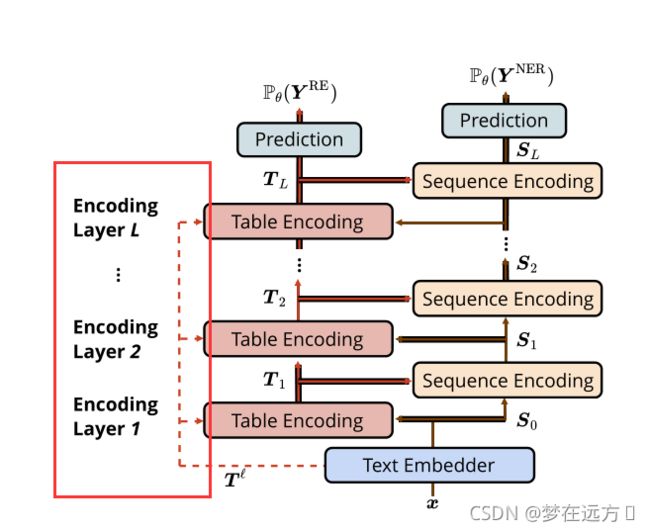
整个Table Encoder部分由多个Table Encoding的单元组成，每个Encoding单元的输入分别是预训练模型的Attention Weight （$T^l$）（后面会提到，这里的公式表示里暂时不加）,对应senquence结构的输入$S$,以及上一个Table Encoding单元的输出$T$

这一部分是用来提取表格的表示信息，这个表格的第i行第j列的向量对应于输入句子的第i个和第j个单词的Embedding合并一起，再送入一个全连接层得到一个大小减半（和单个词的Embedding维度相同）的结果。然后送入Relu。第一个Table Encoder直接使用的为Text Embedder的结果，后面使用的为前一个Table Encoder输出的结果。用公式表达这个过程为：
$$X_{l,i,j}=\mathrm{ReLU}\left(\mathrm{Linear}\left(\left[S_{l-1,i};S_{l-1,j}\right]\right)\right)$$
Table Encoding 采用MDRNN结构提取输入的特征信息，作者在这选择MDGRU（多维度GRU）

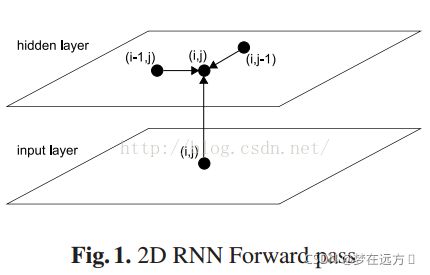
放一张纵向图方便理解：

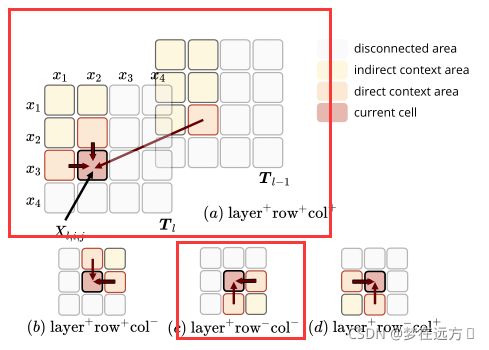
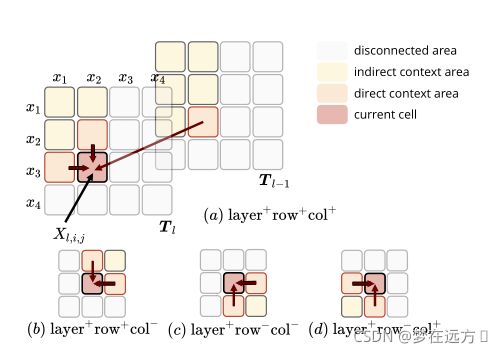
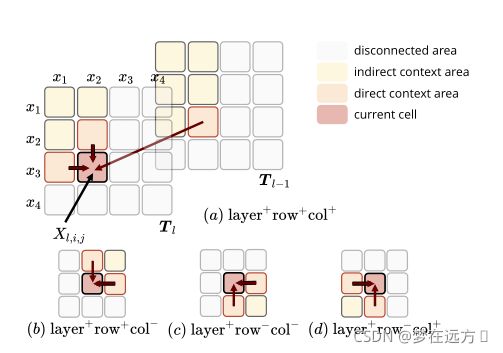
上图所示为计算MDRNN的4个方向，一般来说，它沿着层、行和列的维度利用上下文。也就是说，它不仅考虑相邻的行和列的单元格，而且还考虑上一层的单元格。对于其中一个方向的计算，我们就需要一个方向的GRU来完成。公式表达如下：
$$T_{l,i,j}=\mathrm{GRU}\left(X_{l,i,j},T_{l-1,i,j},T_{l,i-1,j},T_{l,i,j-1}\right)$$

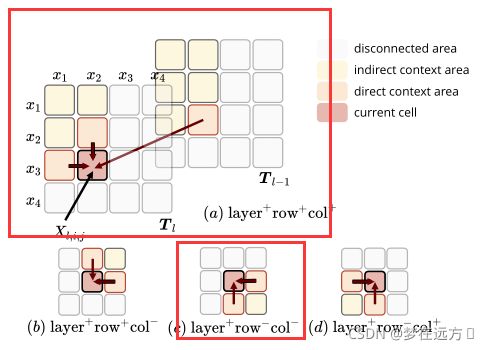
但是作者在具体实现的时候，依据经验以及最后所做的实验认为只需要考虑(a),©两种情况，就可以达到一个和考虑全部四种情况近似的效果（多考虑两种在效果上提升不大，加大了模型参数，也可能出现过拟合现象），作者在论文中直接使用了只考虑两种情况来作为最后的选用。

$$\begin{array}{l}{T}_{l,i,j}^{(a)}={\mathrm{GRU}}^{(a)}\left(X_{l,i,j},T_{l-1,i,j}^{(a)},T_{l,i-1,j}^{(a)},T_{l,i,j-1}^{(a)}\right)\\ T_{l,i,j}^{(c)}={\mathrm{GRU}}^{(c)}\left(X_{l,i,j},T_{l-1,i,j}^{(c)},T_{l,i+1,j}^{(c)},T_{l,i,j+1}^{(c)}\right)\\ T_{l,i,j}=\left[T_{l,i,j}^{(a)};T_{l,i,j}^{(c)}\right]\end{array}$$

3.3 Sequence Encoder

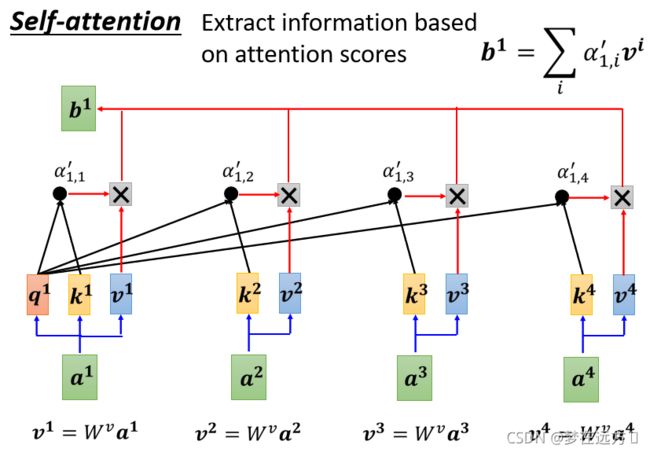
采用了一种类似于Transformer的Encoder的结构，把Multi-head-self-attention换位了Table-Guided Attention，下面，我们着重介绍Table-Guided Attention

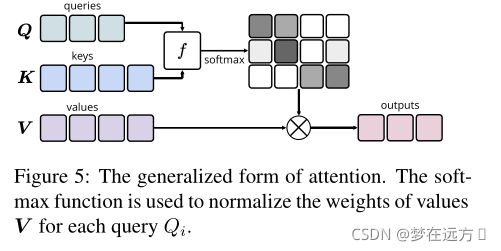
常用的attention的定义如下

其计算方法可以用下面这张图清晰的表示：

用一个简单的公式表示Attention的Weight的计算方式，可以直接用

$$f\left(Q_i,K_j\right)=U\cdot g\left(Q_i,K_j\right)$$
其中U是一个可以学习的向量，g代表我们所设定的Q和K计算相似度的一个计算方法。

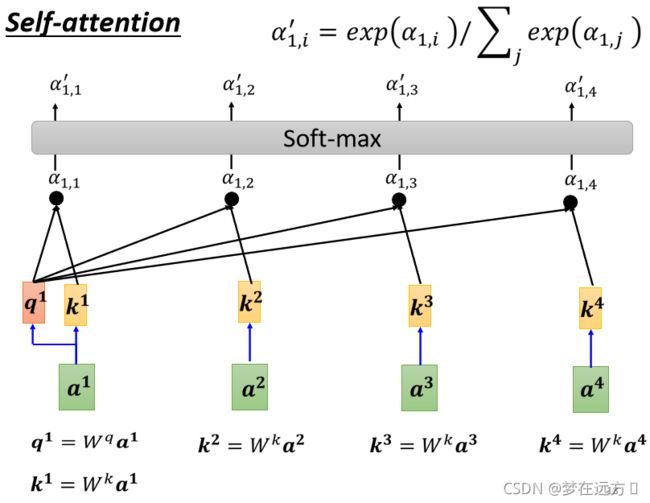
作者在这里使用的是一种Self-attention，其Q,K,V实际上选用了一个相同的值(前一层的输出$S_{l-1}$，也就是$Q=K=V=S_{l-1}$）,由于$T_l$是由多个方向，经过GRU编码而来的，不管从哪个方向都是是由$S_{l-1}$计算而来，因此，我们可以用$T_l$作为上面Attenton公式的$g\left(Q_i,K_j\right)$部分，由此，我们可以得到一个新的公式

$$f\left(Q_i,K_j\right)=U\cdot T_{l,i,j}$$
这样做有三点好处

1. 减少了计算量，不需要计算$T_l$，在Table-Encoder部分就已经完整的进行了计算，只需要存储结果直接访问就好。
2. $T_l$沿着行、列和层维度进行Context，分别对应于Query、key以及前一层中的Query和key。这种上下文信息允许网络更好地捕获更难的词与词之间的依赖关系；
3. 它允许表编码器参与序列表示学习过程，从而形成两个编码器之间的双向交互。

在此基础上作者再引入Multi-head Attention

之后的部分就是和Transformer一样的残差链接(Add)以及LayerNorm操作了。

$$\begin{array}{rl}{\tilde{\mathbf{S}}}_l& =\mathrm{LayerNorm}\left({\mathbf{S}}_{l-1}+\mathrm{SelfAttn}\left({\mathbf{S}}_{l-1}\right)\right)\\ {\mathbf{S}}_l& =\mathrm{LayerNorm}\left({\tilde{\mathbf{S}}}_l+\mathrm{F}\mathrm{F}\mathrm{N}\mathrm{N}\left({\tilde{\mathbf{S}}}_l\right)\right)\end{array}$$

LayerNorm 所做的事情为输入一个向量，输出另外一个向量,它会把输入的这个向量,计算它的均值和标准差

Layer normalization是对同一个feature,不同的dimension,去计算均值和标准差

计算出均值和标准差以后,就可以做一个normalize,我们把input 这个vector裡面每一个,dimension减掉均值,再除以标准差以后得到x’,就是layer normalization的输出
$$x_i^{\prime }=\frac{x_i-m}{\sigma }$$

3.4 Exploit Pre-trained Attention Weights

在前面的讨论中我们忽略了这些虚线。

作者将预训练的Attention Weight作为了Table Encoder的$X_{l,i,j}$的一部分，将原本的
$$X_{l,i,j}=\mathrm{ReLU}\left(\mathrm{Linear}\left(\left[S_{l-1,i};S_{l-1,j}\right]\right)\right)$$
转为了

$$X_{l,i,j}=\mathrm{ReLU}\left(\mathrm{Linear}\left(\left[S_{l-1,i};S_{l-1,j};T_{i,j}^{\ell }\right]\right)\right)$$
其中$T^l$为所有head以及所有层的Attention Weight

作者认为注意力权重的这种简单而新颖的使用，能够有效地将BERT等预训练模型捕获的有用单词-单词交互信息整合到我们的表序列编码器中，从而提高性能。

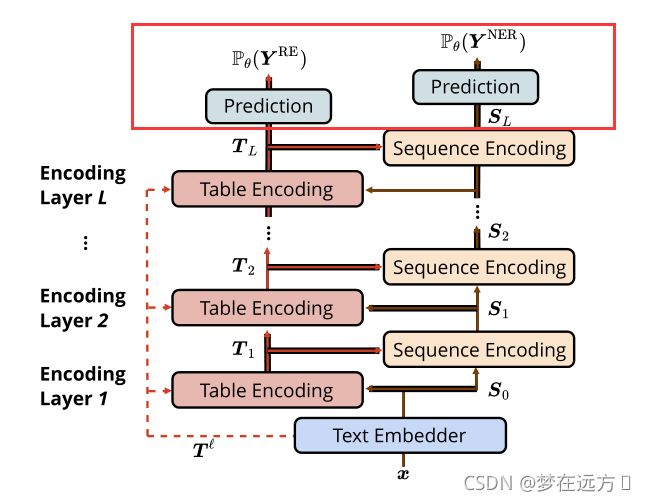
4.训练与验证的过程

$$\begin{array}{rl}{P}_{\theta }\left({\mathbf{Y}}^{\mathrm{N}\mathrm{E}\mathrm{R}}\right)& =\mathrm{softmax}\left(\mathrm{Linear}\left({\mathbf{S}}_L\right)\right)\\ P_{\theta }\left({\mathbf{Y}}^{\mathrm{R}\mathrm{E}}\right)& =\mathrm{softmax}\left(\mathrm{Linear}\left({\mathbf{T}}_L\right)\right)\end{array}$$
分别将最后输出的$S_L$,$T_L$送入Softmax，将输出结果作为实体和关系标签的概率分布：

对于Loss函数的选取，都选用了交叉熵loss，对应的Loss 方程如下：

$$\begin{array}{rl}{\mathcal{L}}^{\mathrm{N}\mathrm{E}\mathrm{R}}& =\sum _{i\in [1,N]}-\log P_{\theta }\left(Y_i^{\mathrm{N}\mathrm{E}\mathrm{R}}=y_i^{\mathrm{N}\mathrm{E}\mathrm{R}}\right)\\ {\mathcal{L}}^{\mathrm{R}\mathrm{E}}& =\sum _{i,j\in [1,N];i\ne j}-\log P_{\theta }\left(Y_{i,j}^{\mathrm{R}\mathrm{E}}=y_{i,j}^{\mathrm{R}\mathrm{E}}\right)\end{array}$$
训练目标就是最小化这两个Loss的和

在用模型进行预测的时候，由于命名实体识别是关系抽取的前提，关系抽取是建立在实体识别之后。我们首先进行命名实体的识别，选择最高概率所对应的class作为识别结果

$$\underset{e}{\mathrm{argmax}}{P}_{\theta }\left(Y_i^{\mathrm{N}\mathrm{E}\mathrm{R}}=e\right)$$
然后预测实体之间是否存在关系：

$$\underset{r}{\mathrm{argmax}}\sum _{i\in \left[i^b,ie\right],j\in \left[j^b,j^e\right]}{P}_{\theta }\left(Y_{i,j}^{\mathrm{R}\mathrm{E}}=r\right)+P_{\theta }\left(Y_{j,i}^{\mathrm{R}\mathrm{E}}=r\right)$$

5.实验过程

5.1 数据与评估指标介绍

论文中选用ACE04,ACE05,CoNLL04,ADE几个数据集来进行模型效果验证。

采用F1 Score来衡量评估模型效果

作者设立了3个F1 Score作为评估

• NER F1 Score：当前仅当实体的类型和边界都与实际的类型和边界相匹配时候，实体的预测才是正确的。
• RE F1 Score：如果关系的类型和两个实体的边界与实际中的关系相匹配，则关系预测被认为是正确的。
• RE+ F1 Score：如果一个关系的类型以及两个实体的边界和类型都与实际数据中的匹配，那么这个关系预测被认为是正确的。

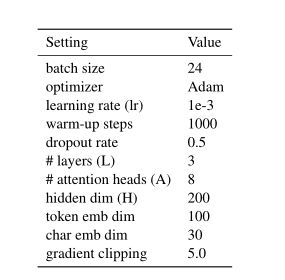
5.2 参数设置

1. 超参数的设置

   

2. 预训练模型使用——Bert的变种ALBERT(没有Fine-tuning)

3. 在Table-Encoder使用了a,c两个情况

   

4. Multi-head的Head数目为8

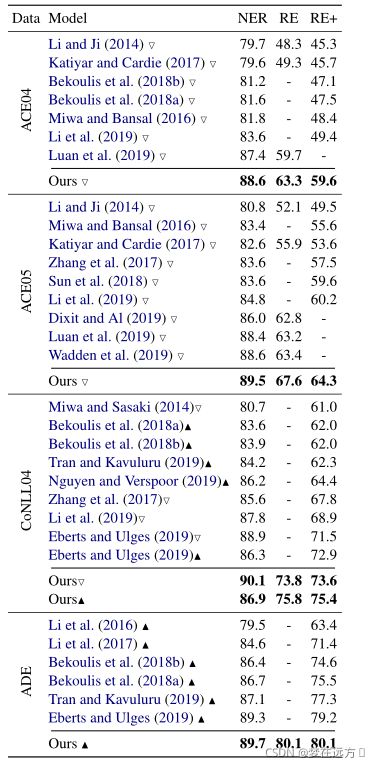
5.3 结果对比

SOTA水平

5.4 使用不同的预训练模型

使用不同的预训练模型会有不一样的效果

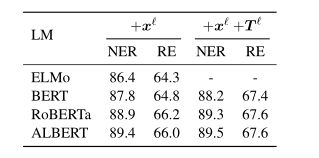
通过没有加入Attention的ELMo模型做实验，结果与之前的SOTA水平相近，说明了作者提出的编码器结构的有效性，并通过Bert，RoBerta,Albert加入了Attention Weight与不加入对比，证明了这一步的有效性。

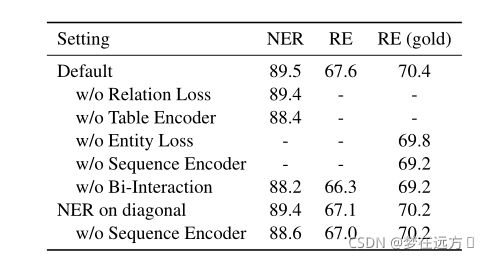
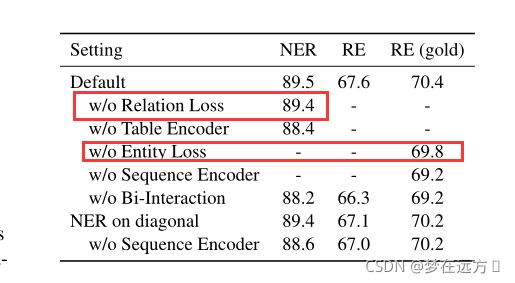
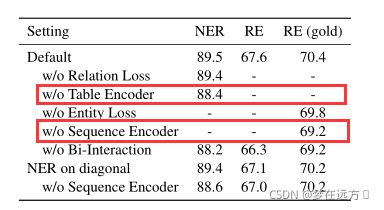
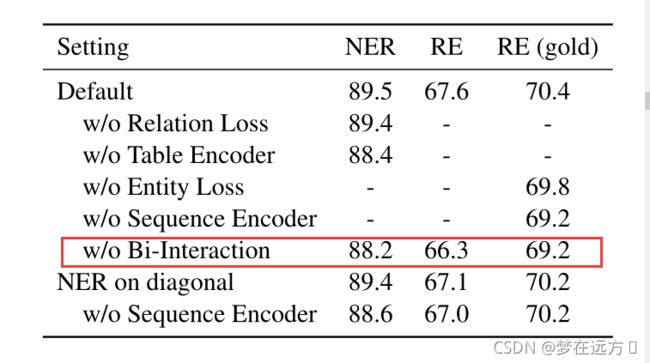
5.5 Ablation Study

利用奥卡姆剃刀理论，作者对组件有效性进行论证

5.5.1 Encoding Layers

1. 首先尝试将两个任务分离，分别去优化NER和RE，对应的结果如下：
   

   可以看到效果变差，这证明将两种任务合二为一是对NER和RE任务有益处的。

2. 然后尝试了值使用一种单独的编码器结果如下：
   
   也尝试了切断两个编码器之间的联系
   
   可以看到，效果都变差了

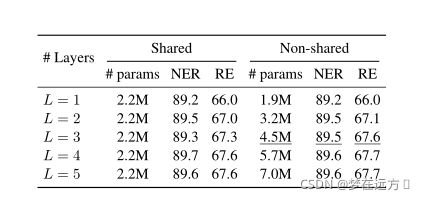
5.5.2 Encoding Layers

作者对Encoding Layer的层数进行了实验，发现当L>3时候，没有明显提升，为了防止出现过拟合现象，作者最终使用了L=3。

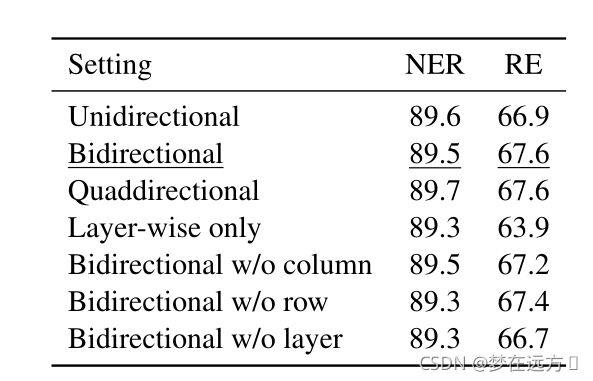
5.5.3 Settings of MD-RNN

Unidirectional 代表在MD-RNN位置只考虑上图(a)的情况

Bidirectional代表在MD-RNN位置只考虑上图(a)©的情况

Quaddirectional 代表在MD-RNN位置考虑上图所有情况

我们发现效果随着考虑信息的增多而变得更好，这说明了富含上下文链接的信息是有益的，此外由于考虑两个方向和四个效果近似，我们仍选用考虑两个方向。

作者也尝试使用CNN代替RNN实现表格编码，但是效果不如RNN（RNN能学到更“远"的信息）

5.6 Attention Visualization

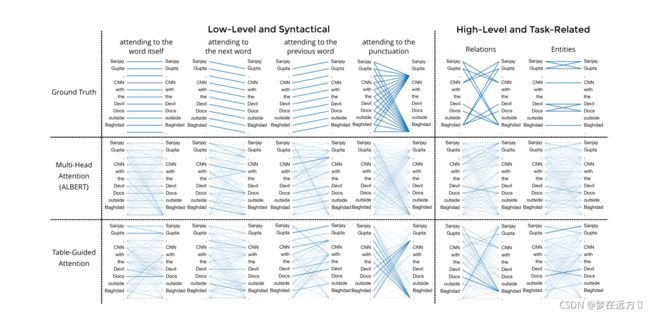
可以看到作者设计的Table-Guided Attention与传统的Multi-head Attention相比，不仅捕捉到了ALBERT未能捕捉到的实体及其关系，而且具有更高的置信度。这表明我们的模型比简单模式具有更强的捕捉复杂模式的能力。

6.总结

本文介绍了一种新颖的表序列编码器结构，用于实体及其关系的联合提取。它学习两个独立的编码器——一个序列编码器和一个表格编码器，两个编码器之间存在显式交互。我们还引入了一种新的方法来有效地利用由预先训练的语言模型捕获的有用信息，用于这种涉及表格表示的联合学习任务。我们在四个标准数据集上获得了NER和ER的SOTA的F1成绩，这证实了我们方法的有效性

7.自己的实验过程

7.1 数据集

由于ACE05数据集没有版权，因此选择了ConLL04数据集进行了实验

7.2 实验环境

开始在自己的1060笔记本实验，后来由于算力限制过于严重(batchsize只能开到1），自费租用了一台NVIDIA Tesla K80的服务器进行了实验

7.3 关键代码查阅

Text Embedder

class AllEmbedding(nn.Module):
    #此处省略了很多部分，我们来看一下核心部分
        
    def forward(self, sentences, return_list=False, return_dict=False):
        embeddings_list = []
        embeddings_dict = {
            'sentences': sentences,
        }
        
        if self.config.char_emb_dim > 0:
            sentences, t_indexs, c_indexs = self.preprocess_sentences(sentences)
            t_indexs = t_indexs.to(self.device)
            c_indexs = c_indexs.to(self.device)
        else:
            sentences, t_indexs, = self.preprocess_sentences(sentences)
            t_indexs = t_indexs.to(self.device)

        # token
        if self.config.token_emb_dim > 0:
            tmp = self.token_embedding(t_indexs)
            embeddings_list.append(tmp)  
            embeddings_dict['token_emb'] = tmp
            
        masks = self.masking(t_indexs, mask_val=0)
        embeddings_dict['masks'] = masks
        
        # char
        if self.config.char_emb_dim > 0:
            c_masks = self.masking(c_indexs, mask_val=0)
            c_lens = c_masks.sum(dim=-1) + (1-masks.long())
            c_embeddings = self.char_embedding(c_indexs)
            c_embeddings = self.char_emb_dropout(c_embeddings)
            c_embeddings = self.char_encoding(c_embeddings, lens=c_lens, mask=c_masks)
            embeddings_list.append(c_embeddings)
            embeddings_dict['char_emb'] = c_embeddings
            
        # lm
        if self.config.lm_emb_dim > 0:
            lm_embs, lm_heads = self.lm_embedding(sentences)
            embeddings_list.append(lm_embs)
            embeddings_dict['lm_emb'] = lm_embs
            if lm_heads is not None:
                embeddings_dict['lm_heads'] = lm_heads
            
        rets = []
            
        if return_list:
            rets += [embeddings_list, masks]
        else:
            embeddings = torch.cat(embeddings_list, dim=-1)
            embeddings_dict['embs'] = embeddings
            rets += [embeddings, masks]
        
        if return_dict:
            rets += [embeddings_dict]
    
        return rets

如上所示，这部分和论文提到的部分一样，作者分别采用了LSTM进行了word Embedding ($x^w$)和 Character Embedding($x^c$)，同时，也是用Bert进行了Word Embedding($x^l$)来使得具有一种语境化的Word Embedding

然后送入了dropout和一个线性层来减少input的维度

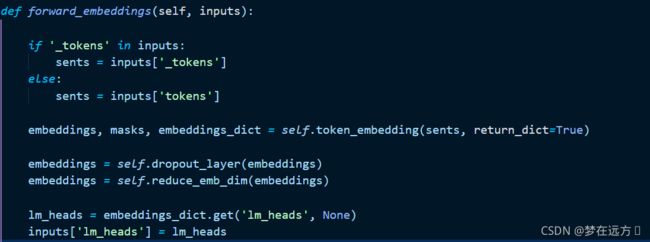
上图最终embeddings存放的便是我们之前提到的${\mathbf{S}}_0=\mathrm{Linear}\left(\left[{\mathbf{x}}^c;{\mathbf{x}}^w;{\mathbf{x}}^{\ell }\right]\right)$

Table Encoder

class TabEncoding(nn.Module):
    """
    省略
    """
    def forward(
        self, 
        S: torch.Tensor, 
        Tlm: torch.Tensor = None,
        Tstates: torch.Tensor = None,
        masks: torch.Tensor = None,
    ):
        
        if masks is not None:
            masks = masks.unsqueeze(1) & masks.unsqueeze(2)
        
        X = self.seq2mat(S, S) # (B, N, N, H)
        X = F.relu(X, inplace=True)
        if self.extra_hidden_dim > 0:
            X = self.reduce_X(torch.cat([X, Tlm], -1))
            X = F.relu(X, inplace=True)
            
        T, Tstates = self.mdrnn(X, states=Tstates, masks=masks)
        
        # the content of T and Tstates is the same;
        # keep Tstates is to save some slice and concat operations
        
        return T, Tstates

Sequence Encoder

class SeqEncoding(nn.Module):
    """
    省略
    """
        
    def forward(
        self, 
        S: torch.Tensor,
        T: torch.Tensor,
        masks: torch.Tensor = None,
    ):
        B, N, H = S.shape
        n_heads = self.n_heads
        subH = H // n_heads
        
        if masks is not None:
            masks = masks.unsqueeze(1) & masks.unsqueeze(2)
            masks_addictive = -1000. * (1. - masks.float())
            masks_addictive = masks_addictive.unsqueeze(-1)
            
        S_res = S
        
        # Table-Guided Attention
        attn = self.linear_qk(T)
        attn = attn + masks_addictive
        attn = attn.permute(0, -1, 1, 2) # (B, n_heads, N, T)
        attn = attn.softmax(-1) # (B, n_heads, N, T)
        
        v = self.linear_v(S) # (B, N, H)
        v = v.view(B, N, n_heads, subH).permute(0, 2, 1, 3) # B, n_heads, N, subH
        
        S = attn.matmul(v) # B, n_heads, N, subH
        S = S.permute(0, 2, 1, 3).reshape(B, N, subH*n_heads)
        
        S = self.linear_o(S)
        S = F.relu(S, inplace=False)
        S = self.dropout_layer(S)
        
        S = S_res + S
        S = self.norm0(S)
        
        S_res = S
        
        # Position-wise FeedForward
        S = self.ffn(S)
        S = self.dropout_layer(S)
        S = S_res + S
        S = self.norm1(S)
        
        return S, attn

7.4 实验结果以及结果分析

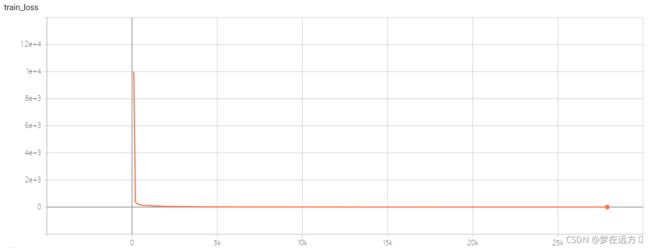
训练的Loss曲线：

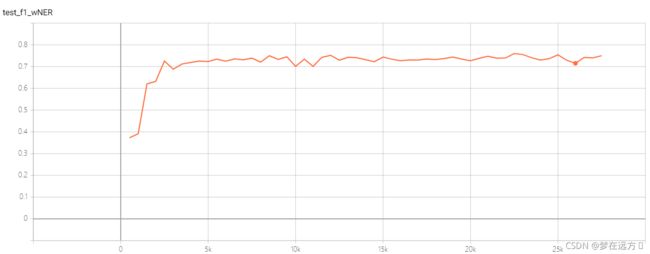
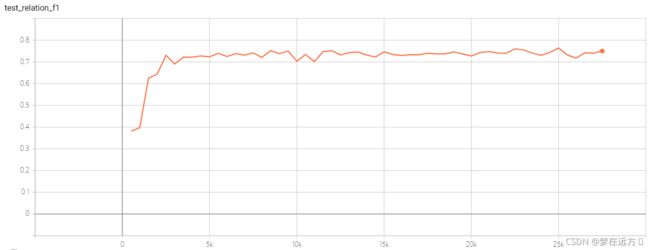
测试集的NER F1 Score:

最高点为0.8985

测试集的RE F1 Score

最高为：0.764

测试集的RE+ F1 Score

最高点为0.7599