MLP与BP
MLP与BP
-
- 1.摘要
- 2.MLP与BP简介
- 3.微分链式法则与计算图
- 4.MLP参数求梯度的闭式解示例
- 5.归纳MLP参数求梯度闭式解的通式
- 6.其他补充
1.摘要
本篇博客主要记录了对前馈神经网络和反向传播算法的简介以及全连接MLP反向传播算法的推导,以便加深理解和记忆。
2.MLP与BP简介
1)MLP模型是由1个输入层,1个输出层,0到多个隐藏层构成的前馈神经网络,每层包含多个MP神经元模型。从层的角度看,每层都可以看作是一个关于输入数据的复合函数;从表示学习的角度看,每一层都为输入数据提供了一个新的表示;从每层的神经元看,每个神经元又可看作独立并行的计算单元,进行分布式处理。
2)由万能近似定理可知,MLP可看作一般函数的通用近似器,由多个线性模型经过激活函数的非线性处理拟合出Borel可测的复杂函数。
3)通过纵深成网络可以减少MP单元的数量,提高可实现性,提高泛化能力,同时也蕴含着联结主义和大型系统由简单构件组成的思想。
4)MLP通过在经验数据上学习,提高计算机程序处理任务的性能度量。其中,学习到的知识就存储在每个互连的MP模型的边上和阈值中。
5)模型学习之初为每个MP模型的边权和阈值设成小随机值,通过模型当前对经验数据的预测值与标记值的均方误差作为损失函数调整各个MP单元的边权和阈值,以达到学习的目的。
6)优化的方法则是采用梯度下降的方法,这时就需要计算损失函数对各个参数(每个MP模型的边权和阈值)的梯度,计算的方法就是反向传播算法backprop,简称BP
3.微分链式法则与计算图
1)微分链式法则
反向传播算法的数学基础就是函数微分的链式法则,是复合函数求微分的方法,这里不多做介绍
2)计算图
计算图语言是描述神经网络更加精确、将计算形式化为图形的一种工具,我们将代数和计算图的表达式称为符号表示
- 图节点:表示一个变量,该变量可以是标量、向量、张量
- 操作:有一个或多个输入,一个输出的函数(不失一般性,该输出可以是多条目的向量、张量)
- 通过多个操作符合在一起描述复杂函数
这里给出一个简单示例

4.MLP参数求梯度的闭式解示例
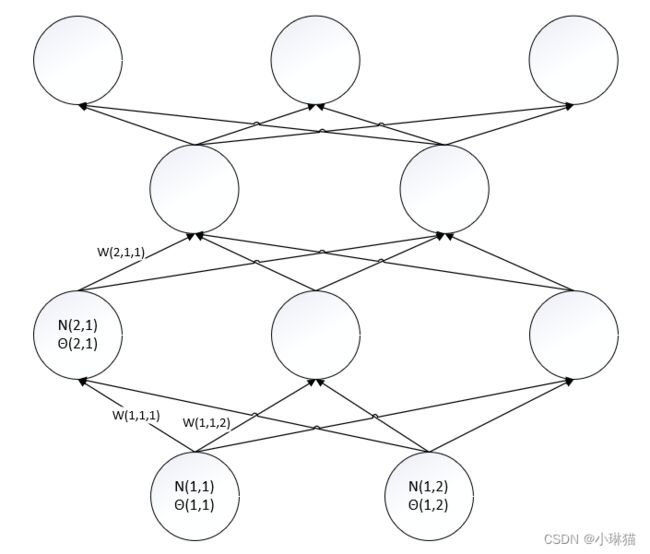
①激活函数:σ,设每个MP单元的激活函数都是σ
②节点:N(i,j),表示第i层第j个MP单元,其中,
N(i,j)节点的输入: N ( i , j ) i n N(i,j)_{in} N(i,j)in, N ( i , j ) i n = ∑ w ( i − 1 , , j ) T N o u t ( i − 1 , ) − θ ( i , j ) N(i,j)_{in} = \sum w(i-1,,j)^T N_{out}(i-1,) - θ(i,j) N(i,j)in=∑w(i−1,,j)TNout(i−1,)−θ(i,j)
N(i,j)节点的输出: N ( i , j ) o u t N(i,j)_{out} N(i,j)out, N ( i , j ) o u t = σ ( ∑ w ( i − 1 , , j ) T N o u t ( i − 1 , ) − θ ( i , j ) ) N(i,j)_{out} = σ(\sum w(i-1,,j)^T N_{out}(i-1,) - θ(i,j)) N(i,j)out=σ(∑w(i−1,,j)TNout(i−1,)−θ(i,j))
当N(i,j)节点为输出层单元时,其标签值为: N ′ ( i , j ) o u t N'(i,j)_{out} N′(i,j)out
③阈值:θ(i,j),表示第i层第i个MP单元的阈值
④边权:w(i,j,k),表示第i层第j个MP单元与第i+1层第k个MP单元之间的边权
⑤损失函数:L(w,θ)
⑥经验数据: X = { x 1 , x 2 , . . . , x n } X =\{x_1,x_2,...,x_n \} X={x1,x2,...,xn}, x i x_i xi是二维向量
1)计算参数数量
参数数 量 w , θ = ( 2 ∗ 3 + 3 ∗ 2 + 2 ∗ 3 ) + ( 2 + 3 + 2 + 3 ) = 28 参数数量_{w,θ} = ( 2 * 3 + 3* 2 + 2 * 3) + ( 2 + 3 + 2 + 3) = 28 参数数量w,θ=(2∗3+3∗2+2∗3)+(2+3+2+3)=28
2)计算w(3,1,1)的梯度(图中红色边权)
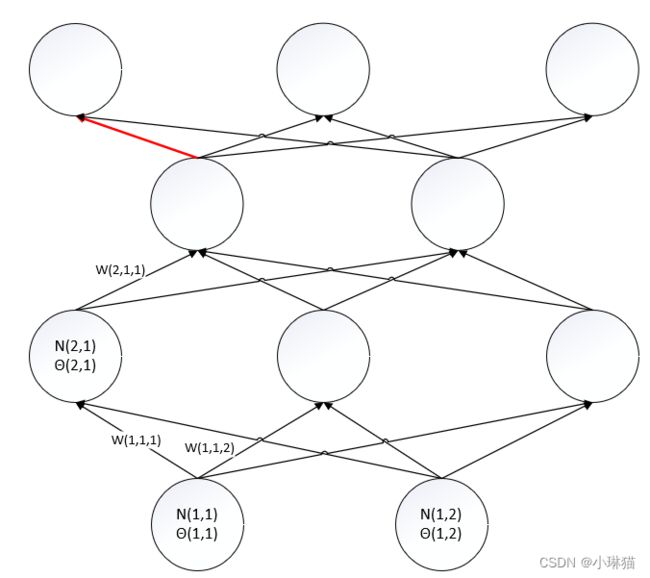
d L ( w , θ ) d w ( 3 , 1 , 1 ) = d L ( w , θ ) d N ( 4 , 1 ) o u t ∗ d N ( 4 , 1 ) o u t d N ( 4 , 1 ) i n ∗ d N ( 4 , 1 ) i n d w ( 3 , 1 , 1 ) \frac {d L(w,θ)} {d w(3,1,1)} = \frac {d L(w,θ)} {d N(4,1)_{out}} * \frac {d N(4,1)_{out}} {d N(4,1)_{in}} * \frac {d N(4,1)_{in}} {d w(3,1,1)} dw(3,1,1)dL(w,θ)=dN(4,1)outdL(w,θ)∗dN(4,1)indN(4,1)out∗dw(3,1,1)dN(4,1)in
更具体地,将每个微分表达式求出,并假设激活函数是sigmoid函数( f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x) = f(x)(1-f(x)) f′(x)=f(x)(1−f(x))),则
d L ( w , θ ) d w ( 3 , 1 , 1 ) = ( N ( 4 , 1 ) o u t − N ′ ( 4 , 1 ) o u t ) ∗ N ( 4 , 1 ) o u t ∗ ( 1 − N ( 4 , 1 ) o u t ) ∗ N ( 3 , 1 ) o u t \frac {d L(w,θ)} {d w(3,1,1)} =(N(4,1)_{out} - N'(4,1)_{out}) * N(4,1)_{out} *(1-N(4,1)_{out}) * N(3,1)_{out} dw(3,1,1)dL(w,θ)=(N(4,1)out−N′(4,1)out)∗N(4,1)out∗(1−N(4,1)out)∗N(3,1)out
3)计算w(2,1,1)的梯度(图中红色边权、黄色边表示可以影响到欲求边权的中间路径)
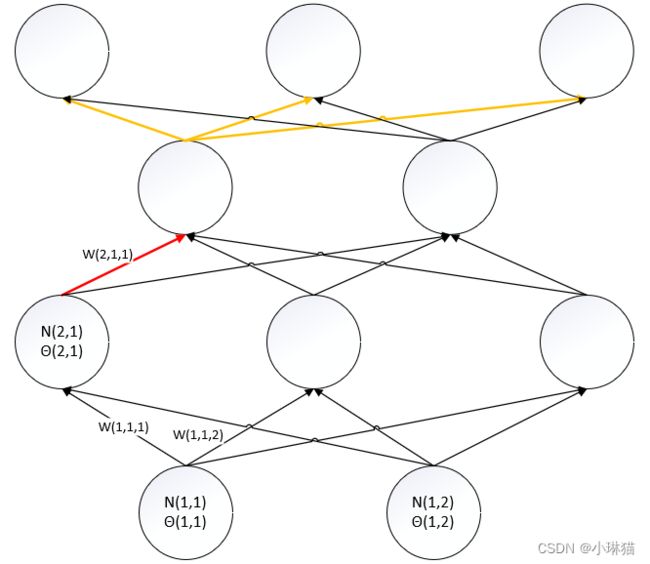
d L ( w , θ ) d w ( 2 , 1 , 1 ) = ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ d N ( 4 , i ) i n d N ( 3 , 1 ) o u t ∗ d N ( 3 , 1 ) o u t d N ( 3 , 1 ) i n ∗ d N ( 3 , 1 ) i n d w ( 2 , 1 , 1 ) = d N ( 3 , 1 ) o u t d N ( 3 , 1 ) i n ∗ d N ( 3 , 1 ) i n d w ( 2 , 1 , 1 ) ∗ ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ d N ( 4 , i ) i n d N ( 3 , 1 ) o u t \frac {d L(w,θ)} {d w(2,1,1)} =\sum_{i}^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \frac {d N(4,i)_{in}} {d N(3,1)_{out}} * \frac {d N(3,1)_{out}} {d N(3,1)_{in}} * \frac {d N(3,1)_{in}} {d w(2,1,1)} \\ = \frac {d N(3,1)_{out}} {d N(3,1)_{in}} * \frac {d N(3,1)_{in}} {d w(2,1,1)} * \sum_{i}^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \frac {d N(4,i)_{in}} {d N(3,1)_{out}} \\ dw(2,1,1)dL(w,θ)=i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗dN(3,1)outdN(4,i)in∗dN(3,1)indN(3,1)out∗dw(2,1,1)dN(3,1)in=dN(3,1)indN(3,1)out∗dw(2,1,1)dN(3,1)in∗i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗dN(3,1)outdN(4,i)in
同2)将微分表达式代入更具体的表示,并假设激活函数是sigmoid函数,则
d L ( w , θ ) d w ( 2 , 1 , 1 ) = N ( 3 , 1 ) o u t ∗ ( 1 − N ( 3 , 1 ) o u t ) ∗ N ( 2 , 1 ) o u t ∑ i 3 ( N ( 4 , i ) o u t − N ′ ( 4 , i ) o u t ) ∗ N ( 4 , 1 ) o u t ∗ ( 1 − N ( 4 , 1 ) o u t ) ∗ w ( 3 , 1 , i ) \frac {d L(w,θ)} {d w(2,1,1)} = N(3,1)_{out} *(1-N(3,1)_{out})*N(2,1)_{out} \sum_{i}^3 (N(4,i)_{out} - N'(4,i)_{out})*N(4,1)_{out} *(1-N(4,1)_{out})*w(3,1,i) dw(2,1,1)dL(w,θ)=N(3,1)out∗(1−N(3,1)out)∗N(2,1)outi∑3(N(4,i)out−N′(4,i)out)∗N(4,1)out∗(1−N(4,1)out)∗w(3,1,i)
下面再求梯度时不再代入更为具体的表示形式
4)计算w(1,1,1)的梯度(图中红色边权、黄色边表示可以影响到欲求边权的中间路径)
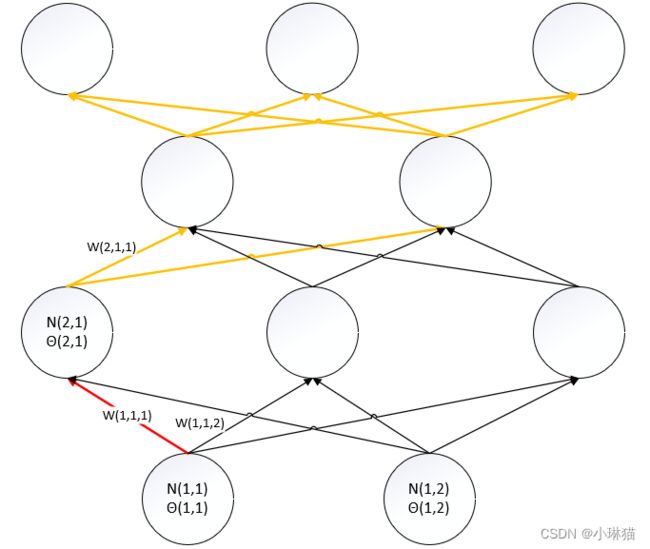
d L ( w , θ ) d w ( 1 , 1 , 1 ) = ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ ∑ j 2 d N ( 4 , i ) i n d N ( 3 , j ) o u t ∗ d N ( 3 , j ) o u t d N ( 3 , j ) i n ∗ d N ( 3 , j ) i n d N ( 2 , 1 ) o u t ∗ d N ( 2 , 1 ) o u t d N ( 2 , 1 ) i n t ∗ d N ( 2 , 1 ) i n d w ( 1 , 1 , 1 ) = d N ( 2 , 1 ) o u t d N ( 2 , 1 ) i n ∗ d N ( 2 , 1 ) i n d w ( 1 , 1 , 1 ) ∗ ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ ∑ j 2 d N ( 4 , i ) i n d N ( 3 , j ) o u t ∗ d N ( 3 , j ) o u t d N ( 3 , j ) i n ∗ d N ( 3 , j ) i n d N ( 2 , 1 ) o u t \frac {d L(w,θ)} {d w(1,1,1)} =\sum_{i}^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \sum_{j}^2 \frac {d N(4,i)_{in}} {d N(3,j)_{out}} * \frac {d N(3,j)_{out}} {d N(3,j)_{in}} * \frac {d N(3,j)_{in}} {d N(2,1)_{out}} * \frac {d N(2,1)_{out}} {d N(2,1)_{int}} * \frac {d N(2,1)_{in}} {d w(1,1,1)} \\ = \frac {d N(2,1)_{out}} {d N(2,1)_{in}} * \frac {d N(2,1)_{in}} {d w(1,1,1)} * \sum_{i}^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \sum_{j}^2 \frac {d N(4,i)_{in}} {d N(3,j)_{out}} * \frac {d N(3,j)_{out}} {d N(3,j)_{in}} * \frac {d N(3,j)_{in}} {d N(2,1)_{out}} dw(1,1,1)dL(w,θ)=i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗j∑2dN(3,j)outdN(4,i)in∗dN(3,j)indN(3,j)out∗dN(2,1)outdN(3,j)in∗dN(2,1)intdN(2,1)out∗dw(1,1,1)dN(2,1)in=dN(2,1)indN(2,1)out∗dw(1,1,1)dN(2,1)in∗i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗j∑2dN(3,j)outdN(4,i)in∗dN(3,j)indN(3,j)out∗dN(2,1)outdN(3,j)in
5)计算θ(4,1)的梯度(绿色为阈值θ对应的MP单元)
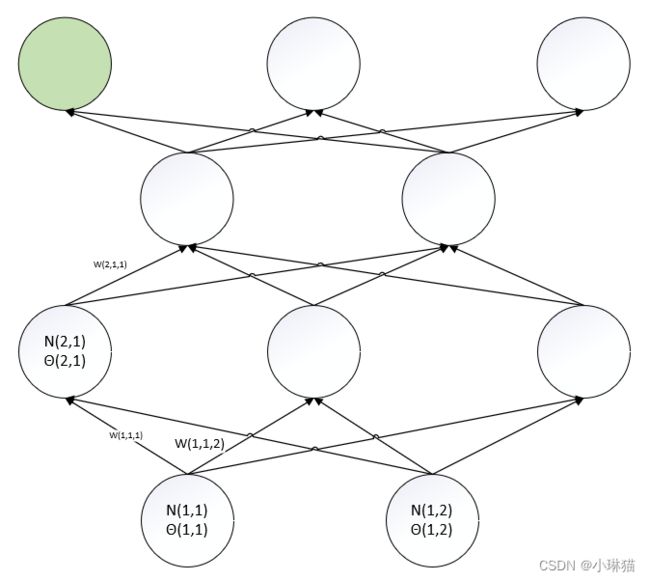
d L ( w , θ ) d θ ( 4 , 1 ) = d L ( w , θ ) d N ( 4 , 1 ) o u t ∗ d N ( 4 , 1 ) o u t d N ( 4 , 1 ) i n ∗ d N ( 4 , 1 ) i n d θ ( 4 , 1 ) \frac {d L(w,θ)} {d θ(4,1)} = \frac {d L(w,θ)} {d N(4,1)_{out}} * \frac {d N(4,1)_{out}} {d N(4,1)_{in}} * \frac {d N(4,1)_{in}} {d θ(4,1)} dθ(4,1)dL(w,θ)=dN(4,1)outdL(w,θ)∗dN(4,1)indN(4,1)out∗dθ(4,1)dN(4,1)in
6)计算θ(3,1)的梯度(绿色为阈值θ对应的MP单元,黄色边表示为可以影响到欲求阈值的中间路径)
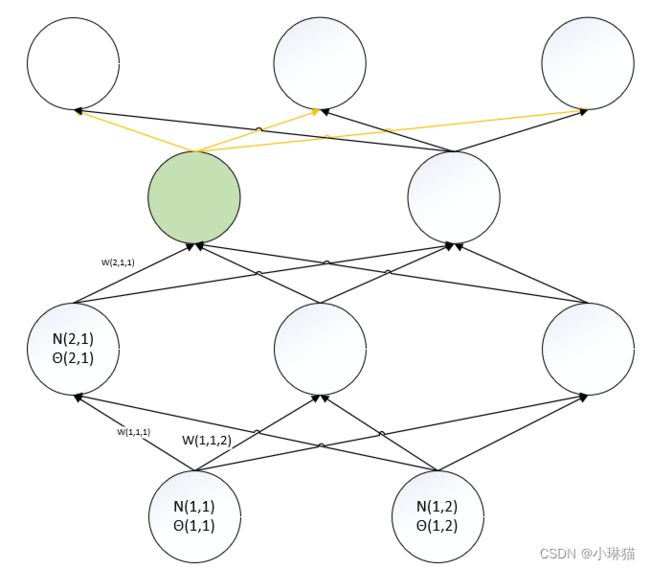
d L ( w , θ ) d θ ( 3 , 1 ) = ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ d N ( 4 , i ) i n d N ( 3 , 1 ) o u t ∗ d N ( 3 , 1 ) o u t d N ( 3 , 1 ) i n ∗ d N ( 3 , 1 ) i n d θ ( 3 , 1 ) = d N ( 3 , 1 ) o u t d N ( 3 , 1 ) i n ∗ d N ( 3 , 1 ) i n d θ ( 3 , 1 ) ∗ ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ d N ( 4 , i ) i n d N ( 3 , 1 ) o u t \frac {d L(w,θ)} {d θ(3,1)} = \sum_i^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \frac {d N(4,i)_{in}} {d N(3,1)_{out}} * \frac {d N(3,1)_{out}} {d N(3,1)_{in}} * \frac {d N(3,1)_{in}} {d θ(3,1)} \\ = \frac {d N(3,1)_{out}} {d N(3,1)_{in}} * \frac {d N(3,1)_{in}} {d θ(3,1)} * \sum_i^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \frac {d N(4,i)_{in}} {d N(3,1)_{out}} dθ(3,1)dL(w,θ)=i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗dN(3,1)outdN(4,i)in∗dN(3,1)indN(3,1)out∗dθ(3,1)dN(3,1)in=dN(3,1)indN(3,1)out∗dθ(3,1)dN(3,1)in∗i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗dN(3,1)outdN(4,i)in
7)计算θ(2,1)的梯度(绿色为阈值θ对应的MP单元,黄色边表示为可以影响到欲求阈值的中间路径)
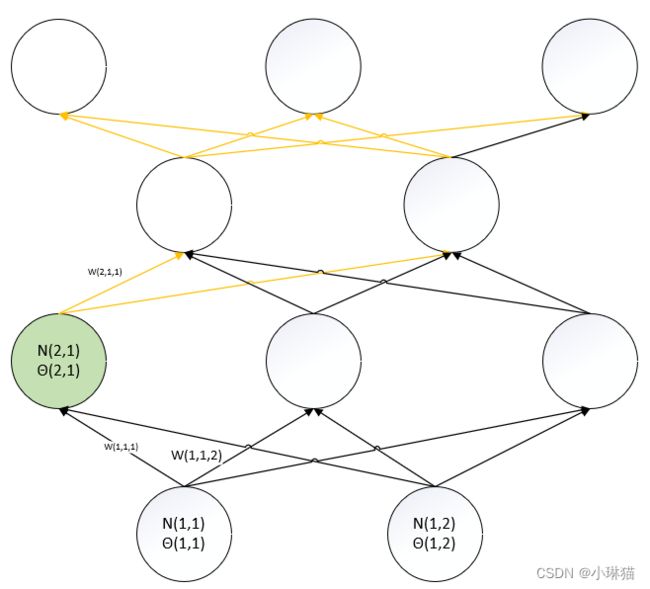
d L ( w , θ ) d θ ( 2 , 1 ) = ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ ∑ j 2 d N ( 4 , i ) i n d N ( 3 , j ) o u t ∗ d N ( 3 , j ) o u t d N ( 3 , j ) i n ∗ d N ( 3 , j ) i n d N ( 2 , 1 ) o u t ∗ d N ( 2 , 1 ) o u t d N ( 2 , 1 ) i n ∗ d N ( 2 , 1 ) i n d θ ( 2 , 1 ) = d N ( 2 , 1 ) o u t d N ( 2 , 1 ) i n ∗ d N ( 2 , 1 ) i n d θ ( 2 , 1 ) ∗ ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ ∑ j 2 d N ( 4 , i ) i n d N ( 3 , j ) o u t ∗ d N ( 3 , j ) o u t d N ( 3 , j ) i n ∗ d N ( 3 , j ) i n d N ( 2 , 1 ) o u t \frac {d L(w,θ)} {d θ(2,1)} = \sum_i^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \sum_j^2 \frac {d N(4,i)_{in}} {d N(3,j)_{out}} * \frac {d N(3,j)_{out}} {d N(3,j)_{in}} * \frac {d N(3,j)_{in}} {d N(2,1)_{out}} * \frac {d N(2,1)_{out}} {d N(2,1)_{in}} * \frac {d N(2,1)_{in}} {d θ(2,1)} \\ = \frac {d N(2,1)_{out}} {d N(2,1)_{in}} * \frac {d N(2,1)_{in}} {d θ(2,1)} * \sum_i^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \sum_j^2 \frac {d N(4,i)_{in}} {d N(3,j)_{out}} * \frac {d N(3,j)_{out}} {d N(3,j)_{in}} * \frac {d N(3,j)_{in}} {d N(2,1)_{out}} dθ(2,1)dL(w,θ)=i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗j∑2dN(3,j)outdN(4,i)in∗dN(3,j)indN(3,j)out∗dN(2,1)outdN(3,j)in∗dN(2,1)indN(2,1)out∗dθ(2,1)dN(2,1)in=dN(2,1)indN(2,1)out∗dθ(2,1)dN(2,1)in∗i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗j∑2dN(3,j)outdN(4,i)in∗dN(3,j)indN(3,j)out∗dN(2,1)outdN(3,j)in
8)计算θ(1,1)的梯度(绿色为阈值θ对应的MP单元,黄色边表示为可以影响到欲求阈值的中间路径)
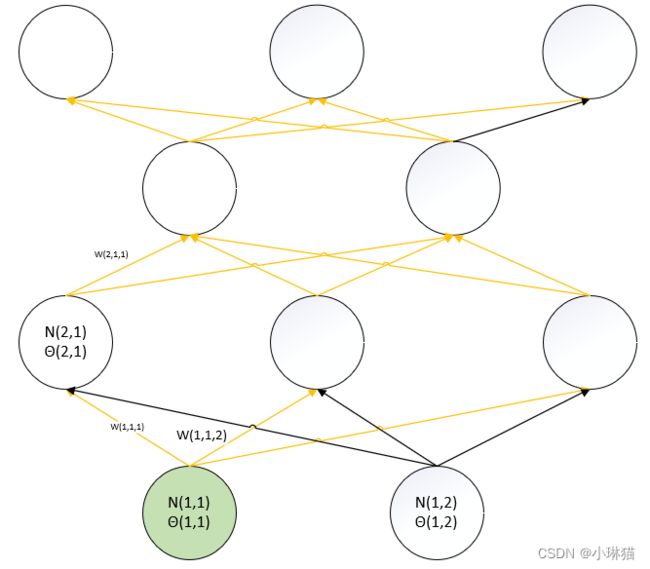
d L ( w , θ ) d θ ( 1 , 1 ) = ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ ∑ j 2 d N ( 4 , i ) i n d N ( 3 , j ) o u t ∗ d N ( 3 , j ) o u t d N ( 3 , j ) i n ∗ ∑ k 3 d N ( 3 , j ) i n d N ( 2 , k ) o u t ∗ d N ( 2 , k ) o u t d N ( 2 , k ) i n ∗ d N ( 2 , k ) i n d N ( 1 , 1 ) o u t ∗ d N ( 1 , 1 ) o u t d N ( 1 , 1 ) i n ∗ d N ( 1 , 1 ) i n d θ ( 1 , 1 ) = d N ( 1 , 1 ) o u t d N ( 1 , 1 ) i n ∗ d N ( 1 , 1 ) i n d θ ( 1 , 1 ) ∗ ∑ i 3 d L ( w , θ ) d N ( 4 , i ) o u t ∗ d N ( 4 , i ) o u t d N ( 4 , i ) i n ∗ ∑ j 2 d N ( 4 , i ) i n d N ( 3 , j ) o u t ∗ d N ( 3 , j ) o u t d N ( 3 , j ) i n ∗ ∑ k 3 d N ( 3 , j ) i n d N ( 2 , k ) o u t ∗ d N ( 2 , k ) o u t d N ( 2 , k ) i n ∗ d N ( 2 , k ) i n d N ( 1 , 1 ) o u t \frac {d L(w,θ)} {d θ(1,1)} = \sum_i^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \sum_j^2 \frac {d N(4,i)_{in}} {d N(3,j)_{out}} * \frac {d N(3,j)_{out}} {d N(3,j)_{in}} * \sum_k^3 \frac {d N(3,j)_{in}} {d N(2,k)_{out}} * \frac {d N(2,k)_{out}} {d N(2,k)_{in}} * \frac {d N(2,k)_{in}} {d N(1,1)_{out}} * \frac {d N(1,1)_{out}} {d N(1,1)_{in}} * \frac {d N(1,1)_{in}} {d θ(1,1)} \\ =\frac {d N(1,1)_{out}} {d N(1,1)_{in}} * \frac {d N(1,1)_{in}} {d θ(1,1)} * \sum_i^3 \frac {d L(w,θ)} {d N(4,i)_{out}} * \frac {d N(4,i)_{out}} {d N(4,i)_{in}} * \sum_j^2 \frac {d N(4,i)_{in}} {d N(3,j)_{out}} * \frac {d N(3,j)_{out}} {d N(3,j)_{in}} * \sum_k^3 \frac {d N(3,j)_{in}} {d N(2,k)_{out}} * \frac {d N(2,k)_{out}} {d N(2,k)_{in}} * \frac {d N(2,k)_{in}} {d N(1,1)_{out}} dθ(1,1)dL(w,θ)=i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗j∑2dN(3,j)outdN(4,i)in∗dN(3,j)indN(3,j)out∗k∑3dN(2,k)outdN(3,j)in∗dN(2,k)indN(2,k)out∗dN(1,1)outdN(2,k)in∗dN(1,1)indN(1,1)out∗dθ(1,1)dN(1,1)in=dN(1,1)indN(1,1)out∗dθ(1,1)dN(1,1)in∗i∑3dN(4,i)outdL(w,θ)∗dN(4,i)indN(4,i)out∗j∑2dN(3,j)outdN(4,i)in∗dN(3,j)indN(3,j)out∗k∑3dN(2,k)outdN(3,j)in∗dN(2,k)indN(2,k)out∗dN(1,1)outdN(2,k)in
5.归纳MLP参数求梯度闭式解的通式
通过上述的示例,我们求出了4层网络中每层对应的4组阈值之一和3组边权之一,这意味着我们可以求出上述示例MLP中任意参数的梯度。
实际上,如果为了推导出全连接MLP任意参数求梯度的通式,仅通过边权和阈值的两组具体求解,我们就已经可以求出通式。费力地写出全部梯度表达式,不仅能更容易归纳,还可以清楚地表明反向传播逐步传播的过程(这与正向传播的顺序恰好相反)
另外,我们发现了一个问题,为何4层网络对应了4组阈值,但只对应了3组边权?实际上,这个问题是因为输出层直接将输出层MP单元的输出值直接参与损失函数的运算,这意味着最后一步输出作为输入的函数及其参数是固定的,不需要再调整了,故只有3组边权。
下面给出任意MLP前馈神经网络求任意参数闭式解的通式
由于我们这里不再限制MLP网络的层数和每层的MP单元数,在4中定义的符号的基础上,我们需增设两个符号定义:
⑦最大层数:m
⑧每层最大单元数: n i , i ∈ { 1 , 2 , . . m } n^i,i∈\{1,2,..m\} ni,i∈{1,2,..m}
1)求w(i,j,k)的梯度
d L ( w , θ ) d w ( i , j , k ) = d N ( i + 1 , k ) o u t d N ( i + 1 , k ) i n ∗ d N ( i + 1 , 1 ) i n d w ( i , j , k ) ∗ ∑ l m n m d L ( w , θ ) d N ( m , l m ) o u t ∗ d N ( m , l m ) o u t d N ( m , l m ) i n ∗ ∑ l m − 1 n m − 1 d N ( m , l m ) i n d N ( m − 1 , l m − 1 ) o u t ∗ d N ( m − 1 , l m − 1 ) o u t d N ( m − 1 , l m − 1 ) i n ∗ . . . ∗ ∑ l i + 2 n i + 2 d N ( i + 3 , l i + 3 ) i n d N ( i + 2 , l i + 2 ) o u t ∗ d N ( i + 2 , l i + 2 ) o u t d N ( i + 2 , l i + 2 ) i n ∗ d N ( i + 2 , l i + 2 ) i n d N ( i + 1 , k ) o u t \frac {d L(w,θ)} {d w(i,j,k)} = \frac {d N(i+1,k)_{out}} {d N(i+1,k)_{in}} * \frac {d N(i+1,1)_{in}} {d w(i,j,k)} * \sum_{l^m}^{n^m} \frac {d L(w,θ)} {d N(m,{l^m})_{out}} * \frac {d N(m,{l^m})_{out}} {d N(m,{l^m})_{in}} * \sum_{l^{m-1}}^{n^{m-1}} \frac {d N(m,{l^m})_{in}} {d N(m-1,{l^{m-1}})_{out}} * \frac {d N(m-1,{l^{m-1}})_{out}} {d N(m-1,{l^{m-1}})_{in}} * ... * \sum_{l^{i+2}}^{n^{i+2}} \frac {d N(i+3,{l^{i+3}})_{in}} {d N(i+2,{l^{i+2}})_{out}} * \frac {d N(i+2,{l^{i+2}})_{out}} {d N(i+2,{l^{i+2}})_{in}} * \frac {d N(i+2,{l^{i+2}})_{in}} {d N(i+1,k)_{out}} dw(i,j,k)dL(w,θ)=dN(i+1,k)indN(i+1,k)out∗dw(i,j,k)dN(i+1,1)in∗lm∑nmdN(m,lm)outdL(w,θ)∗dN(m,lm)indN(m,lm)out∗lm−1∑nm−1dN(m−1,lm−1)outdN(m,lm)in∗dN(m−1,lm−1)indN(m−1,lm−1)out∗...∗li+2∑ni+2dN(i+2,li+2)outdN(i+3,li+3)in∗dN(i+2,li+2)indN(i+2,li+2)out∗dN(i+1,k)outdN(i+2,li+2)in
2)求θ(i,j)的梯度
d L ( w , θ ) d θ ( i , j ) = d N ( i , j ) o u t d N ( i , j ) i n ∗ d N ( i , j ) i n d θ ( i , j ) ∗ ∑ l m n m d L ( w , θ ) d N ( m , l m ) o u t ∗ d N ( m , l m ) o u t d N ( m , l m ) i n ∗ ∑ l m − 1 n m − 1 d N ( m , l m ) i n d N ( m − 1 , l m − 1 ) o u t ∗ d N ( m − 1 , l m − 1 ) o u t d N ( m − 1 , l m − 1 ) i n ∗ . . . ∗ ∑ l i + 1 n i + 1 d N ( i + 2 , l i + 2 ) i n d N ( i + 1 , l i + 1 ) o u t ∗ d N ( i + 1 , l i + 1 ) o u t d N ( i + 1 , l i + 1 ) i n ∗ d N ( i + 1 , l i + 1 ) i n d N ( i , j ) o u t \frac {d L(w,θ)} {d θ(i,j)} = \frac {d N(i,j)_{out}} {d N(i,j)_{in}} * \frac {d N(i,j)_{in}} {d θ(i,j)} * \sum_{l^m}^{n^m} \frac {d L(w,θ)} {d N(m,{l^m})_{out}} * \frac {d N(m,{l^m})_{out}} {d N(m,{l^m})_{in}} * \sum_{l^{m-1}}^{n^{m-1}} \frac {d N(m,{l^m})_{in}} {d N(m-1,{l^{m-1}})_{out}} * \frac {d N(m-1,{l^{m-1}})_{out}} {d N(m-1,{l^{m-1}})_{in}} * ... * \sum_{l^{i+1}}^{n^{i+1}} \frac {d N(i+2,{l^{i+2}})_{in}} {d N(i+1,{l^{i+1}})_{out}} * \frac {d N(i+1,{l^{i+1}})_{out}} {d N(i+1,{l^{i+1}})_{in}} * \frac {d N(i+1,{l^{i+1}})_{in}} {d N(i,j)_{out}} dθ(i,j)dL(w,θ)=dN(i,j)indN(i,j)out∗dθ(i,j)dN(i,j)in∗lm∑nmdN(m,lm)outdL(w,θ)∗dN(m,lm)indN(m,lm)out∗lm−1∑nm−1dN(m−1,lm−1)outdN(m,lm)in∗dN(m−1,lm−1)indN(m−1,lm−1)out∗...∗li+1∑ni+1dN(i+1,li+1)outdN(i+2,li+2)in∗dN(i+1,li+1)indN(i+1,li+1)out∗dN(i,j)outdN(i+1,li+1)in
6.其他补充
1) 通过微分的链式法则可以轻易地得到上述MLP模型中任意参数梯度的闭解,可以计算每一个参数的梯度值,但是在软件的实际实现中每次都重复计算会造成指数级的时间消耗。通过观察,在梯度逆向传播的过程中有许多重复的子表达式,以及重复的正向传播时的计算值。在反向计算梯度时可以将这些值保存下来,通过动态规划减小时间复杂度。
2)反向传播算法实际上不止适用于全连接的MLP网络图,对于任何连接方式的图都可以进行计算。计算时可以通过符号到数值(计算图与表达式)进行计算也可以通过符号到符号(计算图再添加额外的节点)计算。实际上,符号到符号的方法的描述包含了符号到数值的方法,符号到数值的方法可以理解为执行了与符号到符号的方法中构建图的过程中完全相同的计算,只是符号到数值的方法不能显示出计算图。
3)反向传播算法是深度学习计算参数梯度的一种实用方法,但不是唯一方法也不是最优方法。