机器学习-k近邻算法实战

目录

使用k-近邻算法判断性别

1.1构造数据集

1.2 准备数据：从文本文件中解析数据

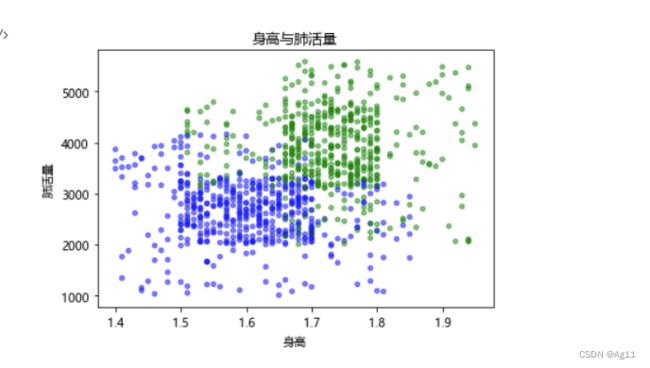
1.3分析数据：用Matplotlib创建散点图

1.4 准备数据：数据归一化

 1.5 KNN实现分类函数

1.6KNN算法的完整实现

1.7实验总结

使用k-近邻算法判断性别

大学生体测包括身高、体重、肺活量，男生和女生在身高体重肺活量上存在差异，若已知一个人的身高体重和肺活量，能否判断一个人的性别。

1.1构造数据集

参考大学生体测标准，设计数据集，数据集共包含一千条数据，男、女各500条数据。其中男女身高在正常范围的数据为400条，偏高偏矮分别50条；体重在正常范围的数据为360条，偏胖偏瘦的各70条；肺活量在正常范围的数据为400条，偏胖偏瘦的各50条。

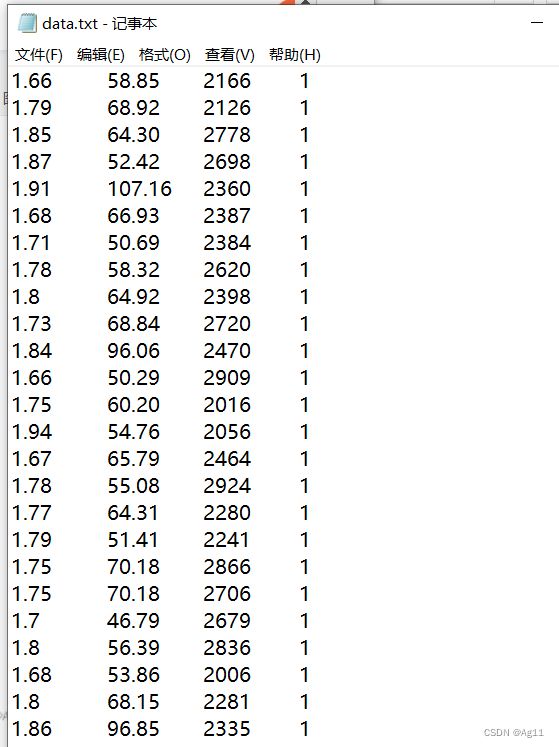
部分数据集截图：

 其中第一列为身高，第二列为体重，第三列为肺活量，第四列为样本标签，1代表性别为男，0代表性别为女

完整数据集：链接：https://pan.baidu.com/s/1EdLbaUYO7SyRbiywKbAloQ 
提取码：kf0m

1.2 准备数据：从文本文件中解析数据

数据集存在在文本文件data.txt中，每个样本数据占据一行，总共有1000行。样本主要包含以下3中特征：

• 身高
• 体重
• 肺活量

 在将上述特征数据输入到分类器之前，必须将待处理数据的格式改变为分类器可以接受的格式。创建名为fileMatrix的函数，以此来处理输入格式问题。该函数的输出为训练样本矩阵和类标签向量。

代码如下：

def fileMatrix():
    file = open("D:\syy\MachineLearning\data\data.txt") # 打开文件
    arrayOLines = file.readlines() # 读取文件
    random.shuffle(arrayOLines) # 将列表中的元素打乱
    numberOfLines = len(arrayOLines) # 得到文件的行数
    returnMat = zeros((numberOfLines, 3)) # 初始化returnMat为一个[numberOfLines,3]的0矩阵
    classLabelVector = [] #存放标签
    index = 0
    for line in arrayOLines:
        line = line.strip() # 一行一行读取数据
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3] #将上一步得到的整行数据分割成一个列表
        classLabelVector.append(int(listFromLine[-1]))
        index += 1
   
    
    return returnMat,classLabelVector

fileMatrix()

1.3分析数据：用Matplotlib创建散点图

代码如下：

def showdatas(datingDatMat, datingLabels, numScatter, xylabel):
    fig = plt.figure()
    font = {'family': 'MicroSoft YaHei'}
    matplotlib.rc("font", **font)
    LabelsColors = []
    for i in datingLabels:
        if i == 0:
            LabelsColors.append('blue')
        if i == 1:
            LabelsColors.append('green')

    ax = fig.add_subplot(111)
    ax.scatter(datingDatMat[:, numScatter[0]], datingDatMat[:, numScatter[1]],color=LabelsColors,s=15, alpha=.5)
    ax.set_xlabel(xylabel[1])
    ax.set_ylabel(xylabel[2])
    plt.title(xylabel[0])
    plt.show()
 
datingDatMat, datingLabels = fileMatrix()
numScatter = array([[0, 1], [0, 2], [1, 2]])
xylabel = array([['身高与体重', '身高', '体重'],
                 ['身高与肺活量', '身高', '肺活量'],
                 ['体重与肺活量', '体重','肺活量']])
showdatas(datingDatMat, datingLabels, numScatter[0], xylabel[0])
showdatas(datingDatMat, datingLabels, numScatter[1], xylabel[1])
showdatas(datingDatMat, datingLabels, numScatter[2], xylabel[2])

 

1.4 准备数据：数据归一化

k-近邻中的距离度量方法为欧氏距离，三维公式为

根据上述公式计算两个样本间的距离时，公式中数字差值属性最大的属性对计算结果的影响最大，在此实例中，肺活量的一般为几千，它对于计算结果的影响将远远大于其他两个特征。但是这三种特征是同等重要的。

在处理这种不同取值范围的特征值时，我们通常采用的方法是将数据归一化，如将取值范围处理为0到1或者-1到1之间

我们可以使用下面的公式将任意取值范围的特征值转化为0到1区间内的值：

newValue = (oldValue-min)/(max-min) 

 其中min和max分别是数据集中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂程度，但为了得到准确结果，我们必须这样做。编写一个autoNorm函数，该函数可以实现数据的归一化

# 数据的归一化
def autoNorm(dataSet):
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m, 1))  #相减
    normDataSet = normDataSet/tile(ranges, (m, 1)) #特征值相除
    return normDataSet, ranges, minVals

 1.5 KNN实现分类函数

 实现原理见上一篇博客：http://t.csdn.cn/Q5oFW

  # inx是测试集，待分类的数据坐标
    # dataset是训练集，即从数据集读取的，已经分类的具有标签的特征 
    # label是整个数据集分类的标签
    # k是KNN，k近邻里面的k
def classify(inx, dataset, labels, k):  
    datasetsize = dataset.shape[0]  # dataSetSize是训练样本集数量

    # tile：把一行inX变成datasetsize行一模一样的,后面的1保证重复完了是datasetsize行，而不是1行里有datasetsize个一样的
    # 然后再减去dataSet，是为了求两点的距离，先要坐标相减，这个就是坐标相减
    # diffmat就是待分类数据特征分别与训练集中每条数据的特征相减的结果
    diffmat = tile(inx, (datasetsize, 1)) - dataset  

    sqdistances = (diffmat ** 2).sum(axis=1)  # axis=1是行相加，这样得到了(x1-x2)^2+(y1-y2)^2+(z1-z2)^2
    distance = sqdistances ** 0.5  # 这样求出来就是欧式距离,distance是存放待分类数据与每条训练集数据的欧式距离的数组

    sorteddistanceindicies = distance.argsort()  # argsort是排序，将元素按照由小到大的顺序返回下标，比如([3,1,2]),它返回的就是([1,2,0])
  
    classcount = {}
    for i in range(k): # 得到欧式距离最近的k个数据的标签,统计每个类别的个数
        votelabel = labels[sorteddistanceindicies[i]] 
        classcount[votelabel] = classcount.get(votelabel, 0) + 1  # 求每个类别的个数，有‘1’就让'1'的计数加1
    sortclass = sorted(classcount.items(), key=operator.itemgetter(1),reverse=True) 
    # classCount.items()将classCount字典分解为元组列表 ,operator.itemgetter(1)按照第二个元素的次序对元组进行排序（第二个元素即每个类别的个数），reverse=True是逆序，即按照从大到小的顺序排列
    return sortclass[0][0]  # 第一个就是最大的，返回最大的类别就是预测的类别

1.6KNN算法的完整实现

数据集中一共有1000条数据，随机选择90%作为训练样本来训练分类器，其余10%测试分类器，检测分类器的准确率

def datingClassTest():
    hoRatio = 0.1   # 10%的测试数据
    datingDatMat, datingLabels = fileMatrix()  # 从文件读数据
    normMat= autoNorm(datingDatMat)              # 数据的归一化
    m = normMat.shape[0]                                           # 所有数据的行数
    numTestVecs = int(m*hoRatio)                                   # 测试数据数量
    errorCount = 0.0                                               # 错误数量统计
    
    for i in range(numTestVecs):
        classifierResult = classify(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 1)
        # print("分类器返回的结果是：%d，真实结果是：%d"%(classifierResult, datingLabels[i]))
        if(classifierResult != datingLabels[i]):
            errorCount += 1.0
        
    print('分类器处理约会数据集的错误率是：%f'%(errorCount/float(numTestVecs)))

datingClassTest()

1.7实验总结

1.7.1 k值的选择

k值	准确率
1	85%
3	89%
5	92%
10	90%
20	91%
100	92%
500	87%

因为测试集和数据集的划分是随机的，所以相同的k值每次运行结果的准确率可能会不同，这里取五次运行准确率的平均结果。通过运行发现，改变k值准确率变化不明显，猜测是因为数据集较大，类别分布平均，且分类特征中存在交集的原因

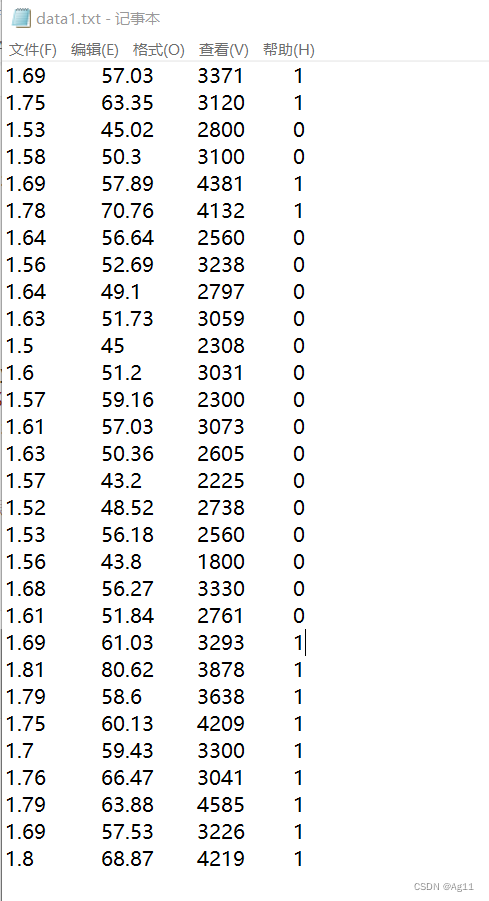
为了验证k值对训练结果的影响，选择30条数据作为数据集，数据集如下：

 

以前五条数据作为测试集，其他数据作为训练集，再次改变k值，可以观察到准确率变化如下：

k值	准确率
1	80%
2	80%
3	100%
5	100%
7	80%
10	80%
20	80%
21	40%
22	40%

1. k = 1时，运行结果如图：

 可以观察到第一条数据的类别错误，原因是k=1时，分类器返回的是训练集中离测试数据最近的那条数据的类别，受此条数据的影响，分类器返回结果为0。

 2.k=3和5时，此时分类器的准确率都为100%，此时的训练效果较好。

3.k>20时，运行结果如下：

分类器的准确率明显下降，原因是训练集中一共只有25条数据，k>20时，返回的是训练集中数量较多的那个类别，在上述数据集中，类别为0的数据多于类别为1的数据，所以分类器返回的结果都是0。

总结：k-近邻算法的结果受样本的影响很大。当选择比较小的K值的时候，表示使用较小领域中的样本进行预测，训练误差会减小，但是会导致模型变得复杂，预测的结果容易受到样本的影响，导致过拟合；当选择较大的K值的时候，表示使用较大领域中的样本进行预测，训练误差会增大，同时会使模型变得简单，容易导致欠拟合；