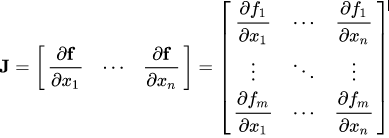PyTorch的自动求导机制详细解析，PyTorch的核心魔法

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

---

作者：Vaibhav Kumar

编译：ronghuaiyang

导读

这篇文章详细解析了PyTorch的自动求导机制，让你了解PyTorch的核心魔法。

在这个过程中，它从不显式地构造整个雅可比矩阵。 直接计算JVP通常更简单、更有效。

我们都同意，当涉及到大型神经网络时，我们都不擅长微积分。通过显式求解数学方程来计算这样大的复合函数的梯度是不现实的，特别是这些曲线存在于大量的维数中，是无法理解的。

要处理14维空间中的超平面，想象一个三维空间，大声地对自己说“14”。每个人都这么做——Geoffrey Hinton

这就是PyTorch的autograd发挥作用的地方。它抽象了复杂的数学，帮助我们“神奇地”计算高维曲线的梯度，只需要几行代码。这篇文章试图描述autograd的魔力。

PyTorch基础

在进一步讨论之前，我们需要了解一些基本的PyTorch概念。

张量：简单地说，它只是PyTorch中的一个n维数组。张量支持一些额外的增强，这使它们独一无二：除了CPU，它们可以加载或GPU更快的计算。在设置.requires_grad = True的时候，他们开始形成一个反向图，跟踪应用于他们的每个操作，使用所谓的动态计算图(DCG)计算梯度(后面会进一步解释)。

在早期版本的PyTorch中，使用torch.autograd.Variable类用于创建支持梯度计算和操作跟踪的张量，但截至PyTorch v0.4.0，Variable类已被禁用。torch.Tensor和torch.autograd.Variable现在是同一个类。更准确地说， torch.Tensor能够跟踪历史并表现得像旧的Variable。

import torch
 import numpy as np
 
 x = torch.randn(2, 2, requires_grad = True)
 
 # From numpy
 x = np.array([1., 2., 3.]) #Only Tensors of floating point dtype can require gradients
 x = torch.from_numpy(x)
 # Now enable gradient
 x.requires_grad_(True)
 # _ above makes the change in-place (its a common pytorch thing)

创建启用梯度的张量的各种方法的代码

注意：根据PyTorch的设计，梯度只能计算浮点张量，这就是为什么我创建了一个浮点类型的numpy数组，然后将它设置为启用梯度的PyTorch张量。

Autograd：这个类是一个计算导数的引擎(更精确地说是雅克比向量积)。它记录了梯度张量上所有操作的一个图，并创建了一个称为动态计算图的非循环图。这个图的叶节点是输入张量，根节点是输出张量。梯度是通过跟踪从根到叶的图形，并使用链式法则将每个梯度相乘来计算的。

神经网络和反向传播

神经网络只不过是经过精心调整(训练)以输出所需结果的复合数学函数。调整或训练是通过一种称为反向传播的出色算法完成的。反向传播用来计算相对于输入权值的损失梯度，以便以后更新权值，最终减少损失。

在某种程度上，反向传播只是链式法则的一个花哨的名字—— Jeremy Howard

创建和训练神经网络包括以下基本步骤：

1. 定义体系结构

2. 使用输入数据在体系结构上向前传播

3. 计算损失

4. 反向传播，计算每个权重的梯度

5. 使用学习率更新权重

损失变化引起的输入权值的微小变化称为该权值的梯度，并使用反向传播计算。然后使用梯度来更新权值，使用学习率来整体减少损失并训练神经网络。

这是以迭代的方式完成的。对于每个迭代，都要计算几个梯度，并为存储这些梯度函数构建一个称为计算图的东西。PyTorch通过构建一个动态计算图(DCG)来实现这一点。此图在每次迭代中从头构建，为梯度计算提供了最大的灵活性。例如，对于前向操作(函数)Mul ，向后操作函数MulBackward被动态集成到后向图中以计算梯度。

动态计算图

支持梯度的张量(变量)和函数(操作)结合起来创建动态计算图。数据流和应用于数据的操作在运行时定义，从而动态地构造计算图。这个图是由底层的autograd类动态生成的。你不必在启动训练之前对所有可能的路径进行编码——你运行的是你所区分的。

一个简单的DCG用于两个张量的乘法会是这样的：

带有requires_grad = False的DCG

图中的每个点轮廓框是一个变量，紫色矩形框是一个操作。

每个变量对象都有几个成员，其中一些成员是：

Data：它是一个变量持有的数据。x持有一个1x1张量，其值等于1.0，而y持有2.0。z持有两个的乘积，即2.0。

requires_grad：这个成员(如果为true)开始跟踪所有的操作历史，并形成一个用于梯度计算的向后图。对于任意张量a，可以按如下方式对其进行原地处理：a.requires_grad_(True)。

grad: grad保存梯度值。如果requires_grad 为False，它将持有一个None值。即使requires_grad 为真，它也将持有一个None值，除非从其他节点调用.backward()函数。例如，如果你对out关于x计算梯度，调用out.backward()，则x.grad的值为∂out/∂x。

grad_fn：这是用来计算梯度的向后函数。

is_leaf：如果：

1. 它被一些函数显式地初始化，比如x = torch.tensor(1.0)或x = torch.randn(1, 1)(基本上是本文开头讨论的所有张量初始化方法)。

2. 它是在张量的操作之后创建的，所有张量都有requires_grad = False。

3. 它是通过对某个张量调用.detach()方法创建的。

在调用backward()时，只计算requires_grad和is_leaf同时为真的节点的梯度。

当打开 requires_grad = True时，PyTorch将开始跟踪操作，并在每个步骤中存储梯度函数，如下所示：

requires_grad = True的DCG

在PyTorch下生成上图的代码是：

Backward()函数

Backward函数实际上是通过传递参数(默认情况下是1x1单位张量)来计算梯度的，它通过Backward图一直到每个叶节点，每个叶节点都可以从调用的根张量追溯到叶节点。然后将计算出的梯度存储在每个叶节点的.grad中。请记住，在正向传递过程中已经动态生成了后向图。backward函数仅使用已生成的图形计算梯度，并将其存储在叶节点中。

让我们分析以下代码：

import torch
 # Creating the graph
 x = torch.tensor(1.0, requires_grad = True)
 z = x ** 3
 z.backward() #Computes the gradient
 print(x.grad.data) #Prints '3' which is dz/dx

需要注意的一件重要事情是，当调用z.backward()时，一个张量会自动传递为z.backward(torch.tensor(1.0))。torch.tensor(1.0)是用来终止链式法则梯度乘法的外部梯度。这个外部梯度作为输入传递给MulBackward函数，以进一步计算x的梯度。传递到.backward()中的张量的维数必须与正在计算梯度的张量的维数相同。例如，如果梯度支持张量x和y如下：

x = torch.tensor([0.0, 2.0, 8.0], requires_grad = True)
 y = torch.tensor([5.0 , 1.0 , 7.0], requires_grad = True)
 z = x * y

然后，要计算z关于x或者y的梯度，需要将一个外部梯度传递给z.backward()函数，如下所示：

z.backward(torch.FloatTensor([1.0, 1.0, 1.0])

z.backward() 会给出 RuntimeError: grad can be implicitly created only for scalar outputs

反向函数传递的张量就像梯度加权输出的权值。从数学上讲，这是一个向量乘以非标量张量的雅可比矩阵(本文将进一步讨论)，因此它几乎总是一个维度的单位张量，与 backward张量相同，除非需要计算加权输出。

tldr ：向后图是由autograd类在向前传递过程中自动动态创建的。Backward()只是通过将其参数传递给已经生成的反向图来计算梯度。 

数学—雅克比矩阵和向量

从数学上讲，autograd类只是一个雅可比向量积计算引擎。雅可比矩阵是一个非常简单的单词，它表示两个向量所有可能的偏导数。它是一个向量相对于另一个向量的梯度。

注意：在这个过程中，PyTorch从不显式地构造整个雅可比矩阵。直接计算JVP (Jacobian vector product)通常更简单、更有效。

如果一个向量X = [x1, x2，…xn]通过f(X) = [f1, f2，…fn]来计算其他向量，则雅可比矩阵(J)包含以下所有偏导组合：

雅克比矩阵

上面的矩阵表示f(X)相对于X的梯度。

假设一个启用PyTorch梯度的张量X：

X = [x1,x2,…,xn](假设这是某个机器学习模型的权值)

X经过一些运算形成一个向量Y

Y = f(X) = [y1, y2，…,ym]

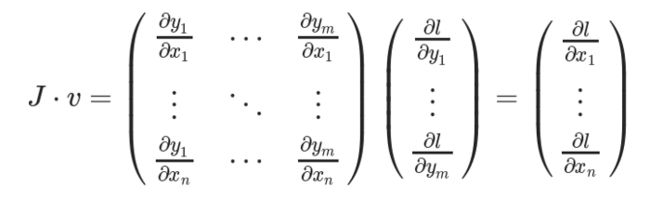
然后使用Y计算标量损失l。假设向量v恰好是标量损失l关于向量Y的梯度，如下：

向量v称为grad_tensor，并作为参数传递给backward() 函数。

为了得到损失的梯度l关于权重X的梯度，雅可比矩阵J是向量乘以向量v

这种计算雅可比矩阵并将其与向量v相乘的方法使PyTorch能够轻松地为非标量输出提供外部梯度。

好消息！

小白学视觉知识星球

开始面向外开放啦

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。


下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。


下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。


交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~