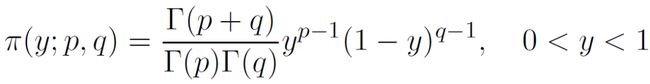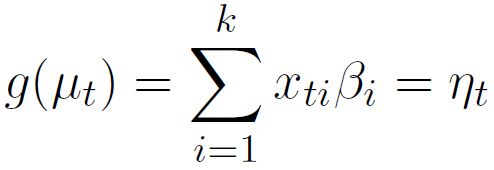logit模型应用实例_广义线性模型应用举例之beta回归及R计算

广义线性模型应用举例之beta回归及R计算 在前文“广义线性模型 ”中，提到广义线性模型(GLM)可概括为服务于一组来自指数分布族的响应变量的模型框架，正态分布、指数分布、伽马分布、卡方分布、 贝塔分布、伯努利分布、二项分布、多项分布、泊松分布、负二项分布、集合分布等都属于指数分布族，并通过极大似然估计获得模型参数。 其中beta回归(beta regression，贝塔回归)是一类用于对来自标准单位区间的连续变量(如比例、百分比数据等)进行建模的广义线性模型，当响应变量服从 beta分布(贝塔分布)时可考虑使用。本篇以比例数据的分析为例，简介beta回归。

比例数据、beta分布与beta回归

在生物学数据分析中，经常会涉及到比例型的数据类型。例如，试验成功的概率(试验成功次数/总次数)，疾病发生频率(人群中患者数/总人数)，物种相对丰度(物种个体数量/群落物种总数)等。比例数据的特点是分布在区间(0, 1)范围内的连续型变量，并且实现了对样本整体某种形式的归一化。    

常见的回归方法应用至比例数据时可能存在局限性

常规的线性回归假定响应变量服从正态分布。比例数据是连续型的数值变量，并且有时一些比例数据也表现出良好的正态分布，似乎可以通过线性回归进行分析，并将获得较合理参数估计以及显著性水平。但更多时候，数值分布大都存在较高的偏离正态性程度，使得线性回归分析比例数据的结果并不理想，回归系数和p值等比较糟糕，变量的生物学意义难以解释。并且基于正态分布的线性回归得出的预测值和置信区间很可能包含比例数据定义区间外的值，即拟合出区间(0, 1)范围外的偏离实际的值。

某些比例数据来自计数型数值的转换。如在群落研究中调查物种丰度时，观察到的物种个体数量是离散型的非负整数，对计数型物种丰度数据的建模，通常泊松回归或负二项回归是优先考虑的。但有时出于特定需要，可能会转换为物种相对丰度(物种个体数量/群落物种总数)用于后续统计分析，此时泊松或负二项回归的局限在于无法应用至小数数值的比例数据中。

比例数据可以为概率响应(如试验成功的概率)，有时形似二项分布试验，容易联想到基于二项分布的logistic回归。但logistic回归要求响应变量为0-1的二分型或非数值的类别型，故不适合连续数值的比例数据分析。    

beta分布与beta回归

beta回归是一种分析比例数据的出色替代方案，其假定响应变量服从beta分布，对于分布在区间(0, 1)范围内的连续型响应变量的建模非常有用。

beta分布

首先来看beta分布，具有beta分布的变量的值是介于0到1之间的连续变量，beta分布的密度函数为：

式中p>0且q>0，Γ(·)是伽马函数(gamma function)，beta分布密度函数的均值E(y)和方差var(y)分别为：

beta分布的密度曲线随均值和方差参数的变化而呈现出许多不同的形状。如下所示了几种代表样式，变量的所有值介于0到1之间，并且分布形状覆盖了各异的均值和离散度水平，而实际上很多生物学数据的变量分布都具有这种beta分布状态的特点。因此，beta分布覆盖面相当广，基于beta分布的beta回归在很多实际问题中有着广泛的应用。

也可以看到，beta分布中某些状态大致与正态分布相同，例如A样式。常规的线性回归假定响应变量服从正态分布，对于呈现A样式beta分布的响应变量，或许可以通过一般线性回归进行参数估计。但若是D、E、F这种，线性回归将会产生较大的偏差。

beta回归

因此，在回归分析中，若响应变量为比例数据，引进beta回归模型进行统计分析顺其自然，并且beta回归模型通常能够较好地对其进行拟合。

beta分布是指数分布族的一员，推广到广义线性模型中就是beta回归。若响应变量Y服从beta分布，则对于给定的一组自变量x_i^T(x_t1, …, x_ti)，Y的条件均值u_t可写作广义线性回归模型：

βi为各自变量x_ti的回归系数。连接函数g(.)存在多种选择，一个最为常见的连接函数是logit连接(logit link)，在这种情况下：

x_i^T即各自变量(x_t1, …, x_ti)，β为各自变量x_ti的回归系数(β₁, …, β_i)。

关于beta回归其它细节，可参考Ferrari和Cribari-Neto(2004)的阐述。

 

文献中使用beta回归的一个实例

上文提到，计数型变量在生物学数据中非常常见，例如物种丰度计数。在广义线性模型中，泊松回归或负二项回归是对这类计数型响应变量建模的常见方法。但有些情况下可能需要转换为物种相对丰度的比例数据进行统计分析，此时泊松回归或负二项回归不适用，就可以考虑beta回归。

因此，不妨首先来看一篇与植物根系微生物组有关研究，将文中涉及到beta回归的部分内容节选出来以帮助大家理解。

Edwards等(2018)研究了连续种植季水稻的根系微生物组。正文Result的第二部分内容中，作者通过特定门水平细菌类群的相对丰度，描述了根系相关微生物在水稻根系的富集模式，包括在土壤到根系区域的空间微尺度层面，以及随水稻根系生长发育的时间层面。

为了明确在细菌门水平上，是否存在特定微生物类群表现出被水稻根系富集或排斥的模式，使用beta回归对它们由土壤-根际-根表-根内(由根外到根内)的相对丰度进行了建模(图2B)。beta回归通过R包betareg执行，各细菌门的相对丰度在这里就作为响应变量对待，选择beta回归的原因就是考虑到各微生物的相对丰度都代表了其来自总微生物群落的相对比例，都是分布在 (0, 1) 区间内的比例数值，beta回归将更加有效。土壤、根际、根表、根内这4个空间微尺度区域是一组有序的类别型自变量，作者对它们分配了一组有序的离散值指代：土壤0、根际1、根表2、根内3。在55个细菌门中，共确定了从根的外部到内部空间分布明显不同的42个门(beta回归中的系数显著)。从土壤环境到根内部，相对丰度显著增加的有20个门(beta回归系数大于0)，代表了它们被水稻根系富集。从土壤环境到根内部，相对丰度降低的有22个门(beta回归系数小于0)，代表了它们被水稻根系排斥。根系排斥的细菌门的回归系数的绝对值总体上更大，表明只有少数比例的土壤微生物由根系富集。

作者还在4个空间微尺度区域内，分别进行了细菌门的相对丰度与水稻年龄的beta回归，以确定哪些微生物表现出明显的随水稻生长的响应(图2C)。观察到不同根系区域中的每个细菌门的丰度随时间表现出近乎一致的趋势。在根表和根内，大多数具有动态丰度模式的细菌类群在水稻生长时期中显著减少(分别为12/22和32/40)，表明在根系发育初期存在大量土壤微生物随机定殖在根系，但最终在与其它类群竞争或者寄主植物选择中被排斥。

原文图2部分。Bulk Soil表示土壤，Rhizosphere表示根际，Rhizoplane表示根表，Endosphere表示根内；Plant Age表示水稻生长时间(天)。

B，beta回归探究不同的细菌门在土壤-根际-根表-根内(由根外到根内)的富集模式，棒棒糖图展示回归系数，回归系数>0为根系富集，<0为根系排斥。

C，beta回归探究不同的细菌门分别在土壤、根际、根表、根内4个区域中随水稻生长时间的富集模式，热图展示回归系数，回归系数>0为根系富集，<0为根系排斥。

   

R包betareg的beta回归分析示例

对于上文列举文献中的beta回归分析，作者在材料方法中提到使用betareg包执行，并同时在附录中提供了分析数据以及R代码。因此不妨就直接使用作者数据，重现文献中该部分的统计分析。

可以在原文附件中获取数据，白鱼同学也已经提前下载下来，存放在百度盘中(提取码，o73b)：

https://pan.baidu.com/s/1cBg-wJwjY6vN_B1W08-euQ

若百度盘失效，也可在GitHub的备份中获取：

https://github.com/lyao222lll/sheng-xin-xiao-bai-yu

数据集概要

下载自原文献Supporting information的附表“S2 Data”(journal.pbio.2003862.s002.xlsx)，记录了所有门水平细菌类群在各样本中的相对丰度信息，以及样本来源对应的水稻种植地区、土壤或根系微尺度区域、水稻生长时间等。

SampleID，样本名称；

Age，取样时对应的水稻生长时间，天；

Site，取样水稻来源的的两个种植地区，California和Arkansas；

Season，取样年份；

Depth，细菌群落研究的目前主要手段是二代扩增子16S测序，该列记录了测序深度，可以理解为对群落调查时抽样观测的物种个体总数；

Phylum2，细菌门水平类群名称，除Proteobacteria因其丰度较高而细分为Alphaproteobacteria、Betaproteobacteria、Deltaproteobacteria等纲水平外，其余均为门水平；

Compartment，取样的空间微尺度位置，其中Bulk Soil表示土壤，Rhizosphere表示根际，Rhizoplane表示根表，Endosphere表示根内；

total_counts，以二代测序reads数为记录的该细菌门中，包含的物种个体数量计数；

RA，该细菌门的相对丰度(relative abundance)，由total_counts(可视为对群落调查时抽样观测的属于该门的物种个体数)除以Depth(可视为对群落调查时抽样观测的物种个体总数)得到的比例值。

该数据集是基于二代扩增子16S测序获得的细菌群落数据，总所周知二代测序的一个问题就是无法保证所有样本的测序深度都相同。通常，为了使以测序reads计数表示的物种丰度计数能够在不同样本间进行横向数值的比较，均一化抽样是在微生物群落数据分析中最常见的处理方式：将所有样本的测序总深度稀释到相同的数量下，也就等同于在相同的观测物种个体总数下进行比较，使reads计数表示的物种丰度计数变得有意义。事实上，对于均一化测序深度后的微生物群落数据而言，计数型的物种丰度或者比例值的相对丰度本质上代表了相同的东西，原则上用哪个都行。然而在这里，作者似乎并没有选择对Depth(测序深度，代表抽样调查的总物种个体数)列中的数值均一化，因此无法直接使用total_counts(测序reads计数，代表抽样调查中属于该门的物种个体数)在各样本间比较，但是RA(以total_counts除以Depth得到的比例值)却是可行的。

该数据集在下文用作beta回归，以重现原文中对根系相关微生物在水稻根系的富集模式的分析。原文中作者分别在土壤到根系区域的空间微尺度层面，以及随水稻根系生长发育的时间层面作了阐述，下文篇幅起见只展示微生物相对丰度由土壤到根系区域变化的beta回归，也就是原文图2B的部分。

先以某细菌门为例展示beta回归运行

文中分析使用的R代码，作者存放在github(https://github.com/bulksoil/LifeCycleManuscript)中，在该链接中找到R文件“diversity2.rmd”，beta回归在第355行开始，同学们有兴趣可自行浏览。

不过作者的原代码中用了大量“%>%”管道符，对于管道符这玩意，白鱼同学的感受一直就是，方便自己书写但不方便别人解读。所以下文就没直接套用作者的原代码，而是作了拆分和更改，虽然看着比先前啰嗦了点但是更方便理解分析过程，并且运行结果不变。

响应变量分布状态的探索

数据集中有几十类细菌门待进行趋势分析，提示要进行批处理。不过在批处理之前，先以其中某个类群为例，展示R函数的运行方法，以及对结果的解读。例如，期望探究Acidobacteria(酸杆菌门)相对丰度是否由土壤到根系发生富集或降低。

#读取数据
dat  
#其中 Compartment 列记录了样本取样的微尺度区域，包含 4 个类别变量
#包括土壤(Bulk Soil)、根际(Rhizosphere)、根表(Rhizoplane)和根内(Endosphere)
levels(dat$Compartment)
#为了探索微生物由土壤到根系的富集模式，需要用离散数值代指有序的土壤-根系区域空间微尺度
#指定 Bulk Soil=0、Rhizosphere=1、Rhizoplane=2、Endosphere=3
dat$compartment_num     ifelse(dat$Compartment == 'Rhizosphere', 1,
       ifelse(dat$Compartment == 'Rhizoplane', 2,
            ifelse(dat$Compartment == 'Endosphere', 3, NA))))
#不妨首先以酸杆菌门(Acidobacteria)为例，展示一些细节
dat_acidobacteria  
#观察 Acidobacteria 相对丰度的分布特征
library(ggplot2)
ggplot(dat_acidobacteria, aes(x = RA, stat(density))) +
geom_histogram(aes(fill = Compartment, color = Compartment), bins = 30, alpha = 0.2) +
geom_line(aes(color = Compartment), stat = 'density', size = 1.5) +
xlim(0, 1)

响应变量Acidobacteria相对丰度的分布特征显示，其大致符合beta分布：是散布在(0, 1) 区间内的比例数值，且分布曲线也体现了beta分布的某种样式。

执行beta回归及对回归系数的生物学意义解释

因此，使用beta回归对Acidobacteria相对丰度与土壤-根系微尺度区域进行建模是可行的。betareg包中，执行beta回归的函数是betareg()。

#探究 Acidobacteria 相对丰度是否由土壤到根系发生富集或降低
#参数详情 ?betareg，不过这里各参数使用默认值(因为看到作者原文中的分析代码，也都是用的默认参数)
library(betareg)
fit_beta summary(fit_beta)  #展示拟合回归的简单统计

输出结果列出了回归系数、回归系数的标准误和参数为0的检验，这些回归参数即可用于对生物学现象的解释。

全模型的R²=0.797，可以理解为变量间的拟合状态比较优秀，Acidobacteria的相对丰度在不同土壤-根系微尺度区域的分布是有规律的。统计显著性通过检验统计量(z值)和相应的p值来表达，p值显示了土壤-根系微尺度区域的回归系数显著，表明Acidobacteria的相对丰度在土壤-根际-根表-根内存在显著差异，并且具有较明显的递增或递减规律。

若回归系数的p值显著，则相对丰度的增加或降低趋势即可通过回归系数的数值判断，正回归系数代表了Acidobacteria由土壤到根系存在选择性的富集，而负回归系数代表了Acidobacteria被根系排斥。这里显示土壤-根系微尺度区域的回归系数为-0.769，即表明Acidobacteria丰度由根外到根内是降低的，可解释为Acidobacteria所涵括的细菌物种中，绝大多数可能对水稻生长无益而被植物选择性的过滤掉，或者在根系与其它微生物物种的竞争中处于劣势而减少，或者在代谢上或环境适应能力上尚不支持在根系的大量定殖等。

对于截距项，就是自变量为0时的响应变量的值，在这里即对应了土壤(定义值为0)中期望的Acidobacteria相对丰度，是有意义的。

双变量关系的散点图辅助理解

如存在疑惑，不妨绘制散点图展示土壤、根际、根表或根内所有样本中Acidobacteria相对丰度的分布，并通过R函数predict()拟合各土壤-根系微尺度区域下期望的Acidobacteria相对丰度后，将拟合值添加在图中以折线连接以形象可视化Acidobacteria相对丰度由土壤到根系的降低趋势。

#可通过 predict() 根据已知回归模型预测 Acidobacteria 在各土壤-根系微尺度区域取样样本中的期望丰度
acidobacteria_pred head(acidobacteria_pred)
#作图查看 Acidobacteria 相对丰度由土壤到根系的降低趋势
library(ggplot2)
dat_acidobacteria$pred pred  
ggplot(data = dat_acidobacteria) +
geom_boxplot(aes(compartment_num, RA, color = Compartment), alpha = 0.5, width = 0.2, outlier.alpha = 0) +
geom_jitter(aes(compartment_num, RA, color = Compartment), alpha = 0.5, width = 0.2, size = 0.7) +
geom_line(data = pred, aes(compartment_num, pred)) +
scale_color_manual(values = c('#4C4C4C', '#688A21', '#3F68E1', '#B02121'),
    limits = c('Bulk Soil', 'Rhizosphere', 'Rhizoplane', 'Endosphere')) +
scale_x_continuous(breaks = c(0, 1, 2, 3), labels = c('0\nBulk Soil', '1\nRhizosphere', '2\nRhizoplane', '3\nEndosphere')) +
theme(panel.grid = element_blank(), panel.background = element_blank(),
    axis.line = element_line(color = 'black'), legend.position = 'none') +
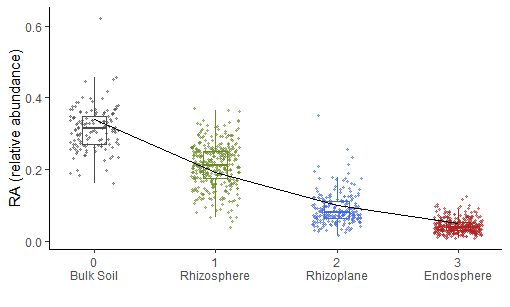
labs(x = '', y = 'RA (relative abundance)')

Bulk Soil表示土壤，Rhizosphere表示根际，Rhizoplane表示根表，Endosphere表示根内；散点和箱线图代表了观测样本中实际的Acidobacteria相对丰度，折线为beta回归对Acidobacteria相对丰度的拟合值。

轻而易见地观察到Acidobacteria相对丰度由根外到根内的逐层衰减。

回归结果中重要内容项的提取

此外，对于重要的内容项，如回归系数、截距、显著性p值、或者其它感兴趣的信息等，如要从中提取，可以如下操作，其它仿照着来即可不再多说了。

#通过 names() 可查看统计结果中包含的内容项，便于从中选择关注的信息
fit_summary names(fit_summary)
#然后结合 $ 从中提取需要的信息，例如
fit_summary$coefficients$mean[1,1]  #截距项
fit_summary$coefficients$mean[1,4]  #截距项的显著性
fit_summary$coefficients$mean[2,1]  #微尺度区域的回归系数
fit_summary$coefficients$mean[2,4]  #微尺度区域的回归系数的显著性
fit_summary$coefficients$precision[1,1]  #phi 的参数估计值
fit_summary$coefficients$precision[1,4]  #phi 的显著性

批处理运行所有细菌门的beta回归

通过上述对某特定细菌门类群的beta回归分析举例，初步了解了R函数的使用、回归参数的生物学意义解读。在大致理解了之后，接下来就对数据集中所有几十类细菌门进行批处理，执行它们相对丰度由土壤-根际-根表-根内(由根外到根内)的趋势分析，并提取回归系数、回归系数标准误、显著性p值、phi参数值等输出为列表，以用于后续的生物学解释。

#处理运行所有细菌门的 beta 回归

dat
result for (phylum in unique(dat$Phylum2)) {
dat_phylum phylum_beta coefficient phi
result_phylum term result_phylum result_phylum$phylum result }
head(result)
#输出结果表格，可以比较和原文附录中提供的回归系数、显著性等统计结果，是完全一致的
write.table(result, 'compartment_beta.txt', sep = '\t', quote = FALSE, row.names = FALSE)
#仿照原文，使用棒棒糖图对根系相关细菌门的可视化
#显著富集或降低的用实心点展示，不显著的用空心点展示
select select[which(select$'Pr(>|z|)' < 0.05),'sig'] select[which(select$'Pr(>|z|)' >= 0.05),'sig']
select select$phylum
ggplot(select, aes(phylum, Estimate)) +
geom_segment(aes(x = phylum, xend = phylum, y = 0, yend = Estimate)) +
geom_point(aes(shape = sig)) +
scale_shape_manual(values = c(1, 16)) +
theme_bw() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))

GN04和WS2这两个微生物门有问题，不知为啥运行后会报错，就直接踢除了，剩余共计55个细菌门(除了Proteobacteria分为几个纲记录)。巧的是，原文也提到总计55个细菌门(或纲)，和最初表格中的57个有出入，估计也是剔除了这两个类群后的统计。

所得结果输出在本地表格中，记录了各细菌门的回归系数、回归系数的标准误、显著性等信息。类似的，根据beta回归系数的显著性和正负值，判断这些微生物中哪些被根系富集或排斥。您还可以选择对回归系数的p值作个进一步的p值校正，获得更稳健的值。

并且由于所有细菌门的回归中，自变量都是统一的尺度，因此也不难想到更大的回归系数对应了更高相对丰度的类群。和原文献结果一致，观察到根系排斥的细菌门的回归系数的绝对值总体上更大，表明只有少数比例的土壤微生物由根系富集，而其它绝大多数可能对水稻生长无益而被植物选择性的过滤掉，或者在根系与其它微生物物种的竞争中处于劣势而减少，或者在代谢上或环境适应能力上尚不支持在根系的大量定殖等。

棒棒糖图是模仿原文图2B的出图，展示了计算的55个细菌门(纲)的回归系数和显著性信息。根据该图即可轻松观察哪些微生物类群是根系相关的，受根系影响的程度，及其相对丰度高低的概况等。和原文图2B的小区别在于，原文基于校正后的p值，而我直接使用原始p值直接绘制的。

此外，您还可以下载原文献补充材料的附表“S3 Data”(journal.pbio.2003862.s003.xlsx)进行比较，该附表是文中图2B、C的作图源数据，也就是作者执行beta回归后的原始输出，同样包括回归系数和截距的参数估计、回归系数的标准误、显著性p值等内容。

上文示例的所有输出值和该附表中的值是完全一致的，同学们自行比较即可，总之完全重现了原文中通过beta回归对特定微生物在土壤-根系微尺度区域的富集模式的分析。

参考资料

https://hansjoerg.me/2019/05/10/regression-modeling-with-proportion-data-part-1/ Edwards J, Santosmedellin C, Liechty Z, et al. Compositional shifts in root-associated bacterial and archaeal microbiota track the plant life cycle in field-grown rice. PLOS Biology, 2018, 16(2). Ferrari S, Cribari-Neto F. Beta Regression for Modelling Rates and Proportions. Journal of Applied Stats, 2004, 31(7):799-815. 友情链接

关于多元回归中需考虑的问题：

变量选择

多重共线性

一般线性模型(LM)：

简单线性回归和多次项回归

多元线性回归(MLR)

带有类别型自变量的线性回归

广义线性模型(GLM)：

计数型响应变量：泊松回归    负二项回归

类别型响应变量：logistic回归

常见的非线性模型：

带交互效应的多元回归

指数回归和线性变换求解

回归树：

随机森林(RF)

Aggregated boosted tree(ABT)

多元回归树(MRT)

生存分析：

非参数方法(Kaplan-Meier曲线)

半参数生存回归(Cox回归)

参数生存回归

基于相似或相异矩阵的回归或降维思想的回归：

基于相似或相异矩阵的多元回归(MRM)

基于成分或特征的回归

偏最小二乘(PLS)回归

冗余分析(RDA)    主响应曲线(PRC)

典范对应分析(CCA)

基于距离的冗余分析(db-RDA)，或称典范主坐标分析(CAP)

结构方程模型(SEM)：

路径分析

验证性因子分析(CFA)

潜变量结构模型

分段结构方程建模