运行软件

activate tensorflow_gpu
jupyter notebook --no-browser --ip=0.0.0.0 --allow-root --NotebookApp.token= --notebook-dir='D:/anaconda3j/upyter_dir/'
jupyter notebook --NotebookApp.token=123 --notebook-dir='D:/anaconda3/upyter_dir/'
决策树
from sklearn import tree
from sklearn.model_selection import train_test_split
Xtrain,Xtest,Ytrain,Ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(Xtrain,Ytrain)
score = clf.score(Xtest,Ytest)
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
import graphviz
dot_data = tree.export_graphviz(clf
,feature_names=feature_name
,class_names=["琴酒","雪莉","贝尔摩德"]
,filled=True
,rounded=True
)
graph = graphviz.Source(dot_data)
graph
clf.feature_importances_
[*zip(feature_name,clf.feature_importances_)]
clf.apply(Xtest)
clf.predict(Xtest)
回归树
在这里插入代码片
numpy用法
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80,1),axis=0)
y = np.sin(X).ravel()
y[::5] += 3*(0.5-rng.rand(16))
plt.figure()
plt.scatter(X,y,s=20,edgecolor="green",c="yellow",label="data")
调参思维
画学习曲线
import matplotlib.pyplot as plt
test = []
for i in range(10):
clf = tree.DecisionTreeClassifier(max_depth=i+1
,criterion="entropy"
,random_state=30
,splitter="random"
)
clf = clf.fit(Xtrain,Ytrain)
score = clf.score(Xtest,Ytest)
test.append(score)
plt.plot(range(1,11)
,test
,color="red"
,label="max_depth"
)
plt.legend()
plt.show()
网格搜索
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split,GridSearchCV,cross_val_score
clf = DecisionTreeClassifier(random_state=25)
gini_threholds = np.linspace(0,0.5,50)
parameters = {
"criterion":("gini","entropy")
,"splitter":("best","random")
,"max_depth":[*range(1,10)]
,"min_samples_leaf":[*range(1,50,5)]
,"min_impurity_decrease":gini_threholds
}
GS = GridSearchCV(clf
,parameters
,cv=10)
GS.fit(Xtrain,Ytrain)
GS
网格搜索重要接口
GS.best_params_
GS.best_score_
泛化误差

影响泛化误差的因素
1)模型复杂度
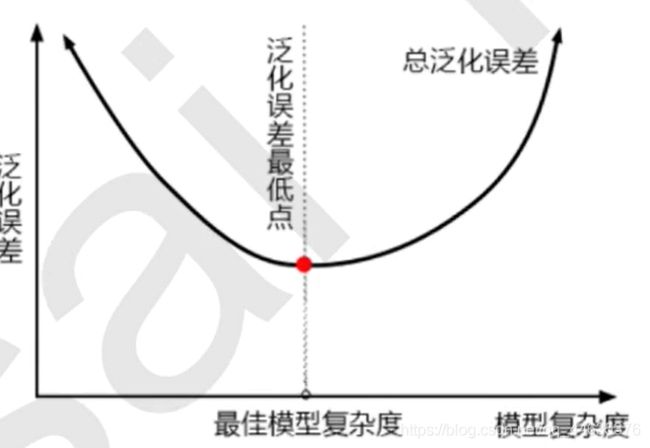
树模型调参策略(按顺序去调)

数据预处理
0、样本不均衡问题
1)采样法解决样本不均衡问题
1.1、上采样
1、无量纲化
1.1线性数据的无量纲化
中心化
缩放处理
归一化:数据变到[0-1]之间
1)归一化
#============================================================数据归一化start==对异常值特别敏感=====================================================
from sklearn.preprocessing import MinMaxScaler
data = np.array([[-1,2],[-0.5,6],[0,10],[1,18]])
# data = [[-1,2],[-0.5,6],[0,10],[1,18]]
#sklearn实现归一化
scaler = MinMaxScaler() #实例化
scaler = scaler.fit(data) #本质是生成min(x)和max(x)
#当data中特征的数量过多,数据量过大时,我们可以使用partial_fit()
#
result = scaler.transform(data) #通过接口导出结果
result
result = scaler.fit_transform(data) #训练和导出结果一步完成
result
scaler.inverse_transform(result) #将归一化后的结果逆转
#使用MinMaxScaler中的参数feature_range=[x,y]实现将数据归一化到除其[0,1]的其他范围中
data = [[-1,2],[-0.5,6],[0,10],[1,18]]
scaler = MinMaxScaler(feature_range=[5,10])
result = scaler.fit_transform(data)
result
2)标准化
from sklearn.preprocessing import StandardScaler
data = np.array([[-1,2],[-0.5,6],[0,10],[1,18]])
scaler = StandardScaler() #实例化
scaler = scaler.fit(data) #本质时生成均值和方差
#接口
scaler.mean_ #查看均值
scaler.var_ #查看方差
x_std = scaler.transform(data) #查看结果
x_std
x_std.mean() #查看均值
x_std.std() #查看标准差
3)选择标准

2、补全缺失值
填补缺失值的专用包:sklearn.impute.SimpleImputer

1)均值填充
#导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
from sklearn.impute import SimpleImputer
#实例化missing_values指定缺失值,指定填充缺失值的方式,这里是平均值
imp_mean = SimpleImputer(missing_values=np.nan,strategy="mean")
#填充X_missing以后返回X_missing_mean
X_missing_mean = imp_mean.fit_transform(X_missing)
X_missing_mean
pd.DataFrame(X_missing_mean)
#确认数据中没有缺失值的方式
pd.DataFrame(X_missing_mean).isnull().sum() #False=0.所以当值为0时,没有控制
2)常数值填充
#常数值填充constant
from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer(missing_values=np.nan,strategy="constant",fill_value=0) #常数值填充参数
X_missing_mean = imp_mean.fit_transform(X_missing)
X_missing_mean
pd.DataFrame(X_missing_mean)
3)随即深林填充缺失值
#这种做法,对于某一个特征大量缺失,其他特征却很完整的情况,非常适用。
#先遍历所有特征,从缺失值最少的特征开始填补,先将其他缺失值用0填补。
X_missing_reg = X_missing.copy()
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values
#argsort返回的是索引
#sort返回的是值
for i in sortindex:
#构建我们的新特征矩阵和新标签
df = X_missing_reg
fillc = df.iloc[:,i]
df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
#在新特征矩阵中,对含有缺失值的列,进行0的填补
df_0 =SimpleImputer(missing_values=np.nan,
strategy='constant',fill_value=0).fit_transform(df)
#找出我们的训练集和测试集
Ytrain = fillc[fillc.notnull()]
Ytest = fillc[fillc.isnull()]
Xtrain = df_0[Ytrain.index,:]
Xtest = df_0[Ytest.index,:]
#用随机森林回归来填补缺失值
rfc = RandomForestRegressor(n_estimators=100)
rfc = rfc.fit(Xtrain, Ytrain)
Ypredict = rfc.predict(Xtest)
#将填补好的特征返回到我们的原始的特征矩阵中
X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = Ypredict
3、编码和哑变量
1)标签编码
#================================================================编码和哑变量===============================================
#标签编码
from sklearn.preprocessing import LabelEncoder
import pandas as pd
# data_ = pd.read_csv(r"Narrativedata.csv"
# ,index_col=0 #指定某一列作为索引
# )
y = data.iloc[:,-1] #要输入的是标签,不是特征矩阵,所以允许一维
le = LabelEncoder() #实例化
le = le.fit(y) #导入数据
label = le.transform(y) #transform接口调取结果
# print(label)
le.classes_ #属性.classes_查看标签中究竟有多少类别
# label #查看获取的结果label
# le.fit_transform(y) #也可以直接fit_transform一步到位
# le.inverse_transform(label) #使用inverse_transform可以逆转
2)特征编码
#特征编码
from sklearn.preprocessing import OrdinalEncoder
#接口categories_对应LabelEncoder的接口classes_,一模一样的功能
data_ = data.copy()
data_.head()
# OrdinalEncoder().fit(data_.iloc[:,1:-1]).categories_ #查看每个特征中有多少个类别
data_.iloc[:,1:-1] = OrdinalEncoder().fit_transform(data_.iloc[:,1:-1])
data_.head()
3)不同变量类型的编码(通常讨论特征变量)
3.1、名义变量的编码(独热编码——>哑变量)
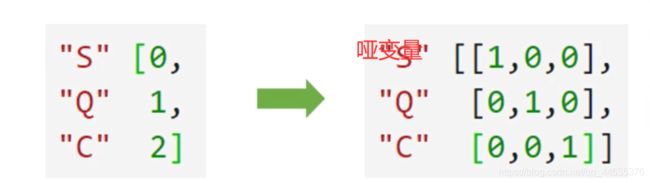
#====================================================针对名义变量的独热编码(获取哑变量)======================================
from sklearn.preprocessing import OneHotEncoder
X = data.iloc[:,1:-1]
enc = OneHotEncoder(categories='auto').fit(X)
result = enc.transform(X).toarray()
result
#依然可以直接一步到位,但为了给大家展示模型属性,所以还是写成了三步
OneHotEncoder(categories='auto').fit_transform(X).toarray() #0.19版本categories必须用列表指定每个特征有多少类,之后的版本写入auto自动识别
#依然可以还原
pd.DataFrame(enc.inverse_transform(result))
enc.get_feature_names() #获取每一列的类别名称
result
result.shape
#axis=1,表示跨行进行合并,也就是将量表左右相连,如果是axis=0,就是将量表上下相连
newdata = pd.concat([data,pd.DataFrame(result)],axis=1)
newdata.head()
# newdata.drop(["Sex","Embarked"],axis=1,inplace=True)
# newdata.columns =
# ["Age","Survived","Female","Male","Embarked_C","Embarked_Q","Embarked_S"]
3.2 有序变量的编码
3.3 有距变量的编码
3.4 比率变量的编码
3.5 连续型变量(特征)的预处理
1)连续型变量的二值化与分段
#=====================连续型变量的二值化与分段========================================================
data_2 = data.copy()
from sklearn.preprocessing import Binarizer
X = data_2.iloc[:,0].values.reshape(-1,1) #Binarizer为特征专用,不能使用一维数组,因此reshape(-1,1)转化为二位数组
X
transformer = Binarizer(threshold = 38).fit_transform(X) #threshold 指定二值化边界
transformer
data_2.iloc[:,0] = transformer
data_2
2)连续型变量划分为分类变量
#=============连续型变量划分为分类变量=====================================================
#preprocessing.KbinsDiscretizer
#n_bins 指定分箱(划分为多少类)数量
#encode 编码类型取值1)onehot:独热编码做哑变量 2)ordinal:整数编码,用不同的整数代替类 3)onehot-dense
#strategy 指定划分策略 1)uniform 等宽(数字大小)分享。 2)quantile 等位(数字数量)分箱 3)kmeans 聚类分箱
from sklearn.preprocessing import KBinsDiscretizer
X = data.iloc[:,0].values.reshape(-1,1)
est = KBinsDiscretizer(n_bins=3
# ,encode="ordinal"
,encode="onehot"
,strategy="uniform"
)
est.fit_transform(X)
# set(est.fit_transform(X).ravel()) #set()转为集和,可以起到去重的作用。ravel()降维函数
est.fit_transform(X).toarray()
4、特征工程

1)特征工程的流程
1:理解业务:根据理解选择特征
2:过滤法,嵌入发,包装发和降维算法选择特征
2)过滤法
2.1、方差过滤(通常只是预处理,过滤掉方差很小或者方差为0的特征)
#=================================================方差过滤=========================================================
#======优先消除方差很小或者方差为0的特征
#threshold 指定方差的阈值,将会删除所有方差小于这个阈值的特征
from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold(threshold=0) #实例化,不填参数threshold默认方差为0
X_var0 = selector.fit_transform(X) #获取删除不合格特征之后的新矩阵
X_var0.shape
=================================
#利用方差过滤只保留一半的特征
import numpy as np
X_fsvar = VarianceThreshold(threshold=np.median(X.var().values)).fit_transform(X)
X_fsvar.shape
=================================
#当特征是二分类时,表示当某种分类占到80%以上时删除该特征
X_bvar = VarianceThreshold(threshold = 0.8*(1-0.8)).fit_transform(X)
X_bvar.shape
2.2、卡方过滤(一种相关性过滤)
#==========卡方过滤==============================================
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest #特征选择的包
from sklearn.feature_selection import chi2 #卡方检验的包
#假设在这里我一直我需要300个特征。k指定需要选择的特征数量(调参对象)
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y)
X_fschi.shape
=====================选取k值得调参方式=================
#画学习曲线
%matplotlib inline
import matplotlib.pyplot as plt
score = []
for i in range(390,200,-10):
X_fschi = SelectKBest(chi2, k=i).fit_transform(X_fsvar, y)
once = cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()
score.append(once)
plt.plot(range(390,200,-10),score)
plt.show()
1)卡方过滤调参之p值调参法(p<0.05或者0.01。我们就认为特征与标签之间相关)
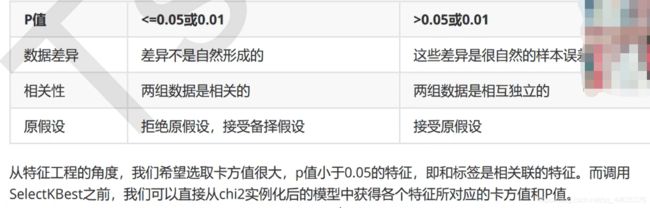
#卡方过滤
chivalue,pvalues_chi = chi2(X_fsvar,y) #获取卡方值k和p值
pvalues_chi
#去除p大于0.05的所有特征
k = chivalue.shape[0] - (pvalues_chi > 0.05).sum()
k
X_fschi = SelectKBest(chi2, k=k).fit_transform(X_fsvar, y)
X_fschi.shape
2.3、F检验和互信息法过滤

#======F检验过滤(线性关系)和互关系法(非线性关系)=========================================
from sklearn.feature_selection import f_classif
#f检验
F,pvalues_f = f_classif(X_fsvar,y)
pvalues_f
k = F.shape[0] - (pvalues_f > 0.05).sum()
k
X_fschi = SelectKBest(f_classif, k=k).fit_transform(X_fsvar, y)
X_fschi.shape

#互信息法
#互信息量【0,1】0表示完全不相关,1表示完全相关
from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(X_fsvar,y)
# k = result.shape[0] - sum(result <= 0)
#X_fsmic = SelectKBest(MIC, k=填写具体的k).fit_transform(X_fsvar, y)
#cross_val_score(RFC(n_estimators=10,random_state=0),X_fsmic,y,cv=5).mean()
2.4、过滤法选择标准

3)嵌入法
3.1、通用
#=======嵌入法=======================================================
#sklearn.feature_selection.SelectFromModel
#重要属性:estimator评估器
#threshold:指定阈值
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier as RFC
RFC_ = RFC(n_estimators =10,random_state=0)
X_embedded = SelectFromModel(RFC_,threshold=0.005).fit_transform(X,y) #在这里我只想取出来有限的特征。0.005这个阈值对于有780个特征的数据来说,是非常高的阈值,因为平均每个特征只能够分到大约0.001的feature_importances_
X_embedded.shape
#====================画嵌入法的学习曲线==================
#模型的维度明显被降低了
#同样的,我们也可以画学习曲线来找最佳阈值
#======【TIME WARNING:10 mins】======#
import numpy as np
import matplotlib.pyplot as plt
RFC_.fit(X,y).feature_importances_
threshold = np.linspace(0,(RFC_.fit(X,y).feature_importances_).max(),20)
score = []
for i in threshold:
X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(X,y)
once = cross_val_score(RFC_,X_embedded,y,cv=5).mean()
score.append(once)
plt.plot(threshold,score)
plt.show()
3.2、嵌入发之逻辑回归的L1正则化(惩罚项)实现降维
1)使用threshold限定系数实现降维
#============此时的判断标准不是l1范数,而是逻辑回归的系数=======================================
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
fullx = []
fsx = []
#此时的判断标准不是l1范数,而是逻辑回归的系数
LR_ = LR(penalty = "l2",solver="liblinear",C=0.9,random_state=420)
threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20)
k=0
for i in threshold:
#降维关键代码
X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
fullx.append(cross_val_score(LR_,data.data,data.target,cv=5).mean())
fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())
# print((threshold[k],X_embedded.shape[1]))
# k+=1
plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label="feature selection")
plt.xticks(threshold)
plt.legend()
plt.show()
2)使用调整l1范数实现降维
#=================================l1范数实现降维==================================================
fullx = []
fsx = []
C=np.arange(0.01,10.01,0.5)
for i in C:
LR_ = LR(solver="liblinear",C=i,random_state=420)
fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target) #norm_order:指定范数是l1范数
fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label="full")
plt.plot(C,fsx,label="feature selection")
plt.xticks(C)
plt.legend()
plt.show()
4)包装法

#=======================================包装法==========================================
# sklearn.feature_selection.RFE (estimator, n_features_to_select=None, step=1, verbose=0)
#接口:.support_: 返回所有的特征是否被选中的bool矩阵 .ranking:返回特征重要性排名
from sklearn.feature_selection import RFE
RFC_ = RFC(n_estimators =10,random_state=0)
selector = RFE(RFC_, n_features_to_select=340, step=50).fit(X, y)
# selector.support_.sum()
# selector.ranking_
X_wrapper = selector.transform(X)
# X_wrapper
cross_val_score(RFC_,X_wrapper,y,cv=5).mean()
#================画学习曲线====================
#画学习曲线
#======【TIME WARNING: 15 mins】======#
score = []
for i in range(1,751,50):
X_wrapper = RFE(RFC_,n_features_to_select=i, step=50).fit_transform(X,y)
once = cross_val_score(RFC_,X_wrapper,y,cv=5).mean()
score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,751,50),score)
plt.xticks(range(1,751,50))
plt.show()
4)降维算法(特征创造,创造的特征无法解释其意义,像类似线性回归等需要解释特征含义的模型,一般不适用降维算法。)
4.1、PCA和SVD
1)降维
#导入包
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
#调用PCA
pca = PCA(n_components=2) #实例化
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X)
X_dr.shape
pca.explained_variance_ #查看可解释性方差大小
pca.explained_variance_ratio_ #查看降维后的新特征占原特征的信息含量比
pca.explained_variance_ratio_.sum() #查看降维后的新特征总信息占原特征总信息的信息含量比
2)数据可视化
#画图
color = ["red","black","orange"]
plt.figure() #实例化画布
for i in set(y):
plt.scatter(X_dr[y == i,0]
,X_dr[y == i,1]
,c = color[i]
,alpha = 0.7
,label=iris.target_names[i])
plt.legend()
plt.title("PCA OF IRIS DATASET")
plt.show()

3)画累计可解释方差贡献率曲线
pca_line
#画累计可解释方差贡献率曲线
import numpy as np
np.cumsum(pca_line) #np.cumsum()实现累加,结果是array([0.92461872, 0.97768521, 0.99478782, 1. ])
plt.plot([1,2,3,4],np.cumsum(pca_line))
plt.xticks([1,2,3,4]) #这是为了限制坐标轴显示为整数
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

4)n_components参数的调整
1、mle自动调整,极大似然估计
pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)
X_mle
pca_mle.explained_variance_ratio_.sum()
2、按信息量占比选择超参数n_components,需要配合参数svd_solver="full"然后n_components的取值在[0,1]之间
#按信息量占比选择超参数,表示要求信息量最少要97%
pca_f = PCA(n_components=0.97,svd_solver="full")
pca_f = pca_f.fit(X)
x_f = pca_f.transform(X)
pca_f.explained_variance_ratio_.sum()
#============返回新的特征空间========================
PCA(n_components=2).fit(X).components_ #返回新的特征空间
4.2、components_在人脸识别中的应用
#人脸识别中components_属性的应用:获取降维后的特征空间
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pylab as plt
import numpy as np
faces = fetch_lfw_people(min_faces_per_person=60) #加载人脸数据
faces.data.shape
#行是样本
#列是样本的所有特征
faces.images.shape
#1348时矩阵中图像的个数
#62是特征的行
#47是特征的列
#图片类数据的数据可视化
X = faces.data
#创建画布fig:就是子图画布,axes:子图对象(画图的操作对象)
fig, axes = plt.subplots(4,5 #指定4行5列共20个图画布
,figsize=[8,4] #指定子图大小
,subplot_kw={"xticks":[],"yticks":[]} #指定子图的坐标轴标签标尺
)
enumerate(axes.flat) #enumerate()将一维数据转化为元组列表,然后方便遍历 .flat:降维的作用
for (i,ax) in enumerate(axes.flat):
ax.imshow(faces.images[i,:,:]
,cmap="gray" #选择颜色模式:gray, spring.......
) #imshow()在子画布上显示图像数据的方法
#components_的作用,新的特征向量(空间坐标系)
#数据降维
pca = PCA(n_components = 150).fit(X)
V = pca.components_
V.shape
#V新的特征空间的数据可视化
fig, axes = plt.subplots(3,8 #指定4行5列共20个图画布
,figsize=[8,4] #指定子图大小
,subplot_kw={"xticks":[],"yticks":[]} #指定子图的坐标轴标签标尺
)
for (i,ax) in enumerate(axes.flat):
ax.imshow(V[i,:].reshape(62,47)
,cmap="gray" #选择颜色模式:gray, spring.......
)
4.3、inverse_transform()不降维去除噪音
#====================使用PCA实现手写数字数据的噪声过滤============================================================
from sklearn.datasets import load_digits
digits = load_digits()
set(digits.target.tolist())
#定义画图函数
def plot_digits(data):
fig,axes = plt.subplots(4,10
,figsize = (10,4)
,subplot_kw = {"xticks":[],"yticks":[]}
)
for i,ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8,8),cmap="binary")
plot_digits(digits.data) #画原始数字
import numpy as np
np.random.RandomState(42)
#==========加噪音=========================
#在指定的数据集中,随机抽取服从正态分布的数据
#两个参数,分别是之数据集和随机抽取出来的正太分布的方差:np.random.normal(数据集,方差)
noisy = np.random.normal(digits.data,2)
plot_digits(noisy)
#===========降噪音========================
pca = PCA(n_components=0.5,svd_solver="full").fit(noisy)
X_dr = pca.transform(noisy)
X_dr.shape
without_noise = pca.inverse_transform(X_dr)
without_noise.shape
plot_digits(without_noise) #画降噪以后的图
线性回归
1、逻辑回归
1)penalty参数(惩罚项|正则化)和C参数


2)逻辑回归代码
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
data = load_breast_cancer()
print(data.data)
X = data.data
y = data.target
data.data.shape
# LR_ = LR(solver="liblinear",C=0.9,random_state=420)
# cross_val_score(LR_,data.data,data.target,cv=10).mean()
# X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
# X_embedded.shape
lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000) #penalty:惩罚项 C:前面的C调整正则化的程度
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000) #逻辑回归的重要属性coef_,查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)
lrl1.coef_ #返回特征对应的参数
(lrl1.coef_ != 0).sum(axis=1)
lrl2 = lrl2.fit(X,y)
lrl2.coef_
(lrl2.coef_ != 0).sum(axis=1)
3)画逻辑回归关于参数C的学习曲线
# 画学习曲线
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420) #拆分训练集和测试集
for i in np.linspace(0.05,1,19):
lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000) #max_iter梯度下降中的迭代次数
lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
lrl1 = lrl1.fit(Xtrain,Ytrain)
l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain)) #accuracy_score(与测试,真实数据)获取预测精准度
l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test] #指定要画的图像值:即将所有的评分结果放入一个列表
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):
plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #图例的位置在哪里?4表示,右下角 loc=i设置图列位置。
plt.yticks(np.arange(0.7,1,0.1))
plt.show()
4)逻辑回归控制梯度下降迭代次数:max_iter=10表示迭代10次。这里画了关于它的学习曲线
l2 = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.arange(1,201,10):
lrl2 = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=i)
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l2,l2test]
color = ["black","gray"]
label = ["L2","L2test"]
plt.figure(figsize=(20,5))
for i in range(len(graph)):
plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i])
plt.legend(loc=4)
plt.xticks(np.arange(1,201,10))
plt.show()
#我们可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
lr = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=300).fit(Xtrain,Ytrain)
lr.n_iter_#array([24], dtype=int32) 只迭代了24次就达到收敛
#n_iter_输出迭代次数
2、逻辑回归求解多分类问题
1)参数mul_class参数

2)参数solver参数

案例1:银行信用评分卡制作
1、数据处理
1)去除重复值
data.drop_duplicates(inplace=True)#inplace=True表示替换原数据
# #删除之后千万不要忘记,恢复索引
data.index = range(data.shape[0])
2)缺失值处理
2.1、探索缺失值
#探索缺失值
data.info()
data.isnull().sum()/data.shape[0]#得到缺失值的比例
#data.isnull().mean()#上一行代码的另一种形式书写
2.1、均值填充缺失值:NumberOfDependents家庭人员数量
data["NumberOfDependents"].fillna(int(data["NumberOfDependents"].mean()),inplace=True)
#这里用均值填补家庭人数这一项
#如果你选择的是删除那些缺失了2.5%的特征,千万记得恢复索引哟~
data.info()
data.isnull().sum()/data.shape[0]
2.2、随即深林填补缺失值:
def fill_missing_rf(X,y,to_fill):
"""
使用随机森林填补一个特征的缺失值的函数
参数:
X:要填补的特征矩阵
y:完整的,没有缺失值的标签
to_fill:字符串,要填补的那一列的名称
"""
#构建我们的新特征矩阵和新标签
df = X.copy()
fill = df.loc[:,to_fill]
df = pd.concat([df.loc[:,df.columns != to_fill],pd.DataFrame(y)],axis=1)
# 找出我们的训练集和测试集
Ytrain = fill[fill.notnull()]
Ytest = fill[fill.isnull()]
Xtrain = df.iloc[Ytrain.index,:]
Xtest = df.iloc[Ytest.index,:]
#用随机森林回归来填补缺失值
from sklearn.ensemble import RandomForestRegressor as rfr
rfr = rfr(n_estimators=100)
rfr = rfr.fit(Xtrain, Ytrain)
Ypredict = rfr.predict(Xtest)
return Ypredict
X = data.iloc[:,1:]
y = data["SeriousDlqin2yrs"]#y = data.iloc[:,0]
X.shape#(149391, 10)
#=====[TIME WARNING:1 min]=====#
y_pred = fill_missing_rf(X,y,"MonthlyIncome")
#注意可以通过以下代码检验数据是否数量相同
# y_pred.shape == data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"].shape
#确认我们的结果合理之后,我们就可以将数据覆盖了
data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"] = y_pred
data.info()
3)异常值处理(通常采用箱线图或者3“segema”法则)
3.1、特征量有限的情况下使用描述性统计处理异常值
#描述性统计
# data.describe()
data.describe([0.01,0.1,0.25,.5,.75,.9,.99]).T #T是转至

1)年龄异常值分析及其处理
#异常值也被我们观察到,年龄的最小值居然有0,这不符合银行的业务需求,即便是儿童账户也要至少8岁,我们可以
# 查看一下年龄为0的人有多少
(data["age"] == 0).sum()
#发现只有一个人年龄为0,可以判断这肯定是录入失误造成的,可以当成是缺失值来处理,直接删除掉这个样本
data = data[data["age"] != 0]
2)违约次数异常的数据分析及其处理
# """
# 另外,有三个指标看起来很奇怪:
# "NumberOfTime30-59DaysPastDueNotWorse"
# "NumberOfTime60-89DaysPastDueNotWorse"
# "NumberOfTimes90DaysLate"
# 这三个指标分别是“过去两年内出现35-59天逾期但是没有发展的更坏的次数”,“过去两年内出现60-89天逾期但是没
# 有发展的更坏的次数”,“过去两年内出现90天逾期的次数”。这三个指标,在99%的分布的时候依然是2,最大值却是
# 98,看起来非常奇怪。一个人在过去两年内逾期35~59天98次,一年6个60天,两年内逾期98次这是怎么算出来的?
# 我们可以去咨询业务人员,请教他们这个逾期次数是如何计算的。如果这个指标是正常的,那这些两年内逾期了98次的
# 客户,应该都是坏客户。在我们无法询问他们情况下,我们查看一下有多少个样本存在这种异常:
# """
data[data.loc[:,"NumberOfTimes90DaysLate"] > 90]
data[data.loc[:,"NumberOfTimes90DaysLate"] > 90].count()
data.loc[:,"NumberOfTimes90DaysLate"].value_counts()
#有225个样本存在这样的情况,并且这些样本,我们观察一下,标签并不都是1,他们并不都是坏客户。因此,我们基
# 本可以判断,这些样本是某种异常,应该把它们删除。
data = data[data.loc[:,"NumberOfTimes90DaysLate"] < 90]
#一定要恢复索引
data.index = range(data.shape[0])
data.info()
3)偏态严重的数据处理
3.1、这里制作评分卡不适用统一量纲
4)样本不均衡问题
4.1、探索样本是否均衡
#探索标签的分布
X = data.iloc[:,1:]
y = data.iloc[:,0]
y.value_counts()#查看每一类别值得数据量,查看样本是否均衡
n_sample = X.shape[0]
n_1_sample = y.value_counts()[1]
n_0_sample = y.value_counts()[0]
print('样本个数:{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample,n_1_sample/n_sample,n_0_sample/n_sample))
#样本个数:149165; 1占6.62%; 0占93.38%
4.2、上采样解决样本不均衡
# %pip install imblearn
#如果报错,就在prompt安装:pip install imblearn
import imblearn
#imblearn是专门用来处理不平衡数据集的库,在处理样本不均衡问题中性能高过sklearn很多
#imblearn里面也是一个个的类,也需要进行实例化,fit拟合,和sklearn用法相似
from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state=42) #实例化,用于上采样
X,y = sm.fit_resample(X,y)
n_sample_ = X.shape[0]#278584
n_sample
pd.Series(y).value_counts()
n_1_sample = pd.Series(y).value_counts()[1]
n_0_sample = pd.Series(y).value_counts()[0]
print('样本个数:{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))
#样本个数:278584; 1占50.00%; 0占50.00%
y.count()
4.3、预处理完成的数据需要存储起来,以便下次使用
from sklearn.model_selection import train_test_split
X = pd.DataFrame(X)
y = pd.DataFrame(y)
X_train, X_vali, Y_train, Y_vali = train_test_split(X,y,test_size=0.3,random_state=420)
model_data = pd.concat([Y_train, X_train], axis=1)#训练数据构建模型
model_data.index = range(model_data.shape[0])
model_data.columns = data.columns
vali_data = pd.concat([Y_vali, X_vali], axis=1)#验证集
vali_data.index = range(vali_data.shape[0])
vali_data.columns = data.columns
model_data.to_csv(r".\model_data.csv")#训练数据
vali_data.to_csv(r".\vali_data.csv")#验证数据
2、分箱操作(离散化连续变量)
略
Kmeans聚类(一种无监督的模型)
![]()


















