通用的改进遗传算法求解带约束的优化问题(MATLAB代码精讲、实际工程经验分享)
目录
- 一、前言
- 二、问题描述
- 三、代码分析
-
- 1、数据结构以及初始化方法
- 2、主程序代码框架
- 3、约束条件的处理
- 4、父代的挑选以及后代解的挑选方法
- 5、调试的一些方法
- 四、运行结果
一、前言
在对多约束、非线性问题的求解上,传统线性规划等方法往往无法有效求解(求解时间过长、无法处理非线性约束等。 进化算法是一类强有力的工具,已经在多个领域有了较为成功的应用。然而,在利用遗传算法、粒子群等等进化算法求解实际的优化问题时,还存在许多困难,具体表现为:
- 1、进化算法难以获得可行解。实际优化问题一般都是超多约束、决策变量类型多样、可行域较小。这种情况下,使用进化算法进行优化求解的情况往往变成,在整个进化过程中,种群都处在不可行域,求解出来的结果也是不可行解,优化失败。或者说,这些迭代过程没有意义。
- 2、进化算法提前收敛,陷入到局部最优。这是进化算法的通病,毕竟是一类概率搜索算法,不能保证每次都收敛到最优解。对于这个问题,也有很多的研究工作,比如niching、crowding distance之类的。对于基本的遗传算法来说,采用轮盘赌或者竞标赛来选择个体,经常会出现所有种群变成一样的情况,这对于优化求解来说是非常不利的。
- 3、进化搜索方向不可掌握。对于进化算法来说,每一次的迭代都是选优的过程。我们很难定义不可行解之间的优劣。比较经典的方法就是计算每个个体违反约束的程度或者是违反约束的次数。然后每次挑选违反约束较小的个体进入下一代。由此来产生进化选择的压力。然而,实际问题往往是,某个约束很难被满足,某些约束较容易被满足。比如微电网中电池的充电次数约束很难被满足,充电功率大小较容易被满足。在进化过程中,我们希望个体满足了充电次数约束之后就不要再违反了,因此这个约束满足之后,很大概率就可以找到可行解。但是,通常情况下,满足这个约束之后,下一次迭代,别的约束被满足的更多,因此就把这个个体舍弃了。那么在我们看来,优化向着反方向去了,这对于收敛来说是不好的。
- 4、代码编写效率低。不知道违反了什么约束,调试起来很费劲。
博主在对许多文章进行复现之后,针对上面提到的问题也是很难受。为了加快复现进度,同时也是给广大研究工作者总结一般的代码编写套路,因此发布一下我经常使用的单目标进化算法框架以及MATLAB代码。本人的研究主要集中在进化多目标优化领域,对于单目标优化问题只是个人兴趣,如有不当,可友好交流讨论。多目标领域的优化之后也会发布一些文章。
二、问题描述
考虑一下下面的优化问题:
m i n y = x 1 2 + x 2 2 min\ y = x_1^2 + x_2^2 min y=x12+x22
约束条件为:
x 1 + x 2 > 1 x 1 − x 2 < 2 x 1 , x 2 ∈ [ − 10 , 10 ] x_1 + x_2 > 1 \\ x_1 - x_2 <2 \\ x_1,x_2 \in [-10,10] x1+x2>1x1−x2<2x1,x2∈[−10,10]
显然,这是一个非常简单的带约束优化问题,一般只能在例子里面见到。经典的遗传算法没有考虑问题存在约束的情况。因此在求解这类带有约束的优化问题时,就需要对遗传算法进行改进,从而提高算法的能力。针对上面提到的几个问题,我们依次进行改进。
三、代码分析
1、数据结构以及初始化方法
在设计种群的数据结构时,以前的遗传算法将个体编码、目标函数值、违反约束的情况其他需要记录的数据单独储存。这样就会程序写起来就会很麻烦,经常出错。并且不好进行调试。
因此,我们参考PlatEMO的数据结构,进行小小的改进。Population里面储存全部的数据。这样,在各个函数之间传递数值时,只需要传递一个struct就够了。创建struct的代码如下:
// Init.m
function Population = Init(PopSize)
% 本函数用于构造初始解
pop.decs=[];
pop.obj=[];
pop.con=[];
pop.detail=[];
Population = repmat(pop,1,PopSize);
for i=1:PopSize
tmp = 10.*rands(1,2);
Population(i).decs = tmp;
end
Population = CalObj(Population);
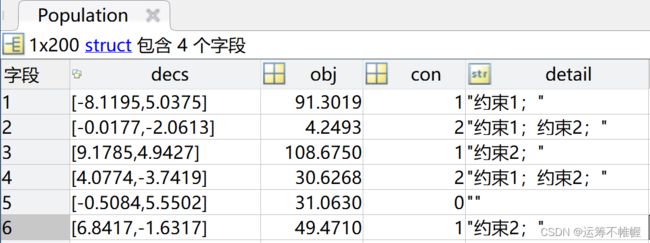
值得注意的是,如果我们想要将里面某一项数据全部取出,需要加中括号。例如:
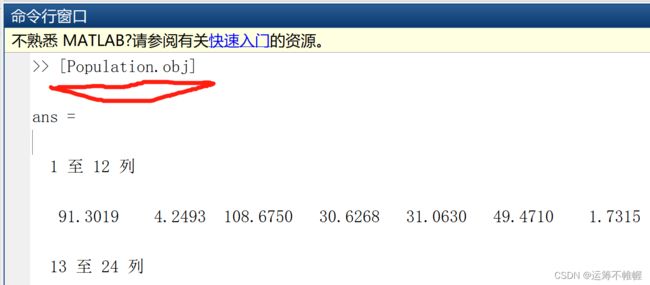
2、主程序代码框架
与传统遗传算法不一样的是,我们精简了程序的流程。主要包括,初始化种群->(挑选父代个体->交叉变异->挑选新一代个体)。括号里面为循环体,进行迭代优化。具体可以看下面的代码。我们将 记录信息、画图等操作集中到RecordInfo()文件中,主程序更加美观。
// Main.m
clear;clc;close all
%% 参数设置
PopSize = 200;
MaxGen = 400;
plt = 1; % 运行过程是否实时画迭代优化图,默认关闭(可极大提高运行速度)
%% 初始化
Population = Init(PopSize);
ConvergenceObj = zeros(2,PopSize);
ConvergenceCon = zeros(2,PopSize);
BestSol = repmat(Population(1),1,MaxGen);
%% 开始优化求解
h = figure();
for gen = 1:MaxGen
MatingPool = TournamentSelection(2,PopSize,[Population.cons],[Population.obj]); %挑选父代
Offspring = GA(Population(MatingPool)); %进行交叉变异操作
Population = EnviornmentalSelection(Population,Offspring,gen/MaxGen); %挑选子代
RecordInfo(); % 记录迭代优化信息
end
3、约束条件的处理
我们研究的这个问题比较简单,只包含了两个约束,所以一旦出现什么问题,也比较好解决。但是,现实问题都是包含几十上百的约束,如果不做好管理,很容易出现混乱。因此我们加了一个约束的描述。可以更加方便的修改。具体来说,在计算目标值之后,接着计算这个个体违反约束的情况。下图代码所示:
// CalObj.m
function Population = CalObj(Population)
% 本函数用于计算种群个体的目标函数值
N = length(Population);
for i=1:N
x = Population(i).decs;
%% 计算目标函数值
f = x(1)^2+x(2)^2;
%% 计算约束违反情况
old_con = 0;
con = 0;
detail = "";
if x(1)+x(2) <= 1
con = con + 1;
end
if con ~= old_con
detail = detail+"约束1;";
old_con = con;
end
if x(1)-x(2)>=2
con = con + 1;
end
if con ~= old_con
detail = detail+"约束2;";
old_con = con;
end
if max(x)>10 || min(x)<-10
con = con + 1;
end
if con ~= old_con
detail = detail+"越界;";
old_con = con;
end
%% 封装数据
Population(i).obj = f;
Population(i).con = con;
Population(i).detail = detail;
end
例子里面目标函数和约束都比较简单,不做过多讲解。
值得注意的是,我们在这里只是判断个体是否违反约束,违反了就加1。在某些情况下,我们也可以考虑违反约束的程度。比如约束是 x < 1 x<1 x<1。那么对于两个个体 x = 2 x=2 x=2和 x = 3 x=3 x=3,虽然他们都是违反约束的,但是显然后者违反的程度更深,我们倾向于选择前者。这都是约束优化的一些改进方法。在计算完目标函数之后,我们就可以观察Population的值了。
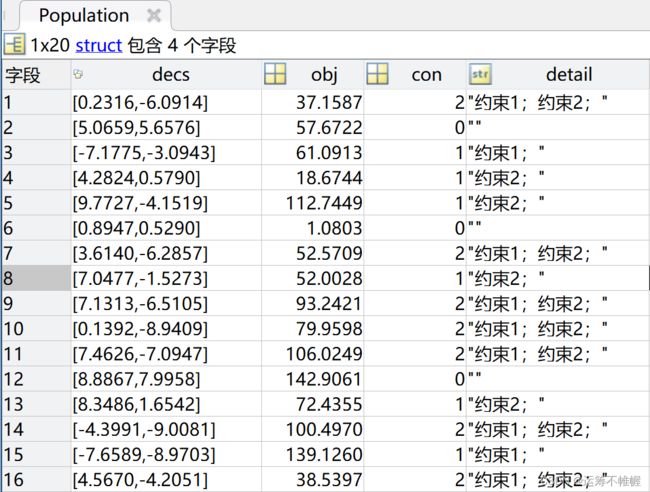
可以看到,种群决策变量、目标函数、违反约束情况一目了然。
4、父代的挑选以及后代解的挑选方法
在主程序里面,我们加入了一个父代解的挑选过程。在经典的遗传算法里面,挑选解的过程没有方向性,导致进化效果较差。参考多目标优化算法NSGA-II里面的竞标赛挑选方法,我们在改进的方法里面也同样使用这个方法来挑选父代个体。具体的过程可以描述如下:每一轮挑选中,我们选择k个个体,然后k个个体里面挑最好的,直到挑够N个。直接使用PlatEMO平台的代码,调用方法为:
// An highlighted block
MatingPool = TournamentSelection(2,PopSize,[Population.con],[Population.obj]);
这里我们设置k=2,N=种群大小。挑选准则为,先看违反约束、再看目标值。这样挑出来的个体具有竞争力,后代个体更容易进化。
在个体进化之后,我们需要进行一轮挑选,以产生进化压力,推动算法向最优值进化。这个过程可以简单的描述为优胜劣汰。对于带约束的优化问题,优劣的描述为:1)如果两个个体都违反约束,那么违反程度小的个体较好;2)如果两个个体一个违反、一个满足,那么满足约束的较好;3)如果两个个体都满足约束,那么,目标函数值小的个体较好。
值得注意的是,为了保证种群个体的多样性,如果我们简单的进行替换,那么种群很快便会全部收缩到一个小区域。这对于算法的搜索是不利的,为了解决这个问题,可以使用一对一的替换方法。也就是说,除非后代比相应的父代个体好,否则不替换。具体如下:
// EnviornmentalSelection.m
function New_Population = EnviornmentalSelection(Population,Offspring,state)
% 本函数用来挑选新的种群
N = length(Population);
New_Population = Population;
%% 基本思路如下:为了确保种群的多样性,采用一对一替换机制。只有后代表现强于父代才会发生替换。
for i=1:N
pcv = Population(i).con;
ccv = Offspring(i).con;
pf = Population(i).obj;
cf = Offspring(i).obj;
if (pcv == 0 && ccv == 0) % 采用 feasible rules 挑选新解
if pf < cf
New_Population(i) = Population(i);
else
New_Population(i) = Offspring(i);
end
else
if pcv < ccv
New_Population(i) = Population(i);
else
New_Population(i) = Offspring(i);
end
end
end
对于种群的多样性保持,有很多研究方法。在multimodal研究的基础上,有些思路非常有意思。之后也搞搞这方面的文章。水很深,把握不住啊。
5、调试的一些方法
在对实际问题进行求解时,很多时候都是前面大量的迭代搜索一直在找可行解。这对于计算资源有限的问题比较麻烦。并且,有时候搜索到最后都不能获得可行解。那就是求解失败。对于这个问题,可以先进行一个尝试性的求解。比如这个问题,我们运行完看一下决策变量的分布情况
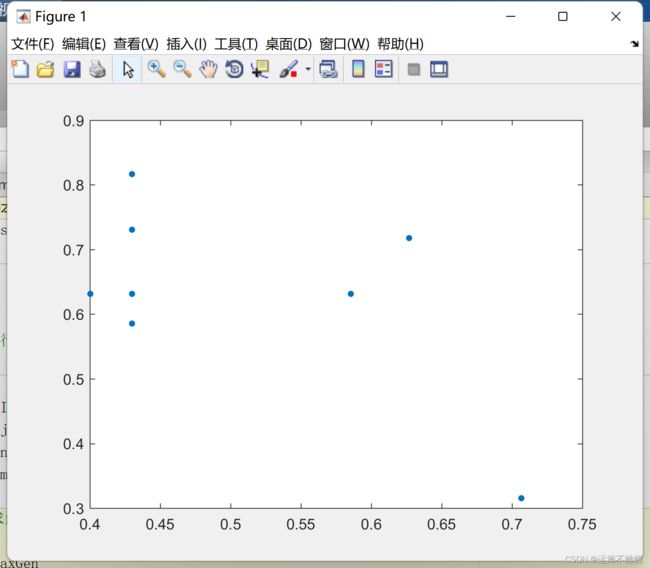
可以看到,解分布在[0.4,0.75],[0.3,0.9]之间,这对于-10~10的决策空间来说,相差非常大。因此我们在生成初始解的时候可以适当的进行贪婪,比如选择50%的个体进行贪婪初始化,让他们分布在更靠近可行解的区域,那么对于求解来说,效率就会大大增加。
四、运行结果
问题较为简单,运行就设置比较小的迭代次数和种群大小。
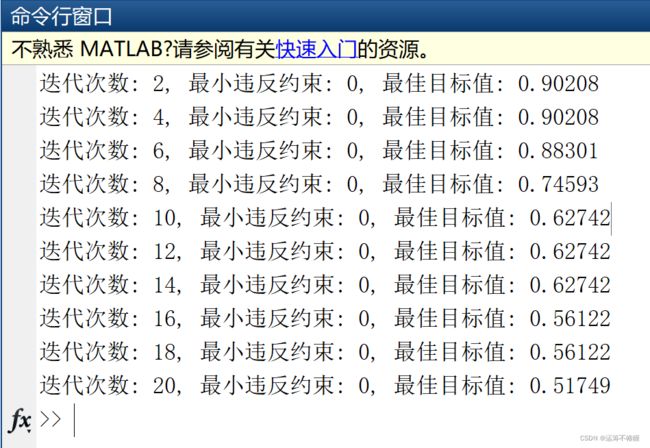
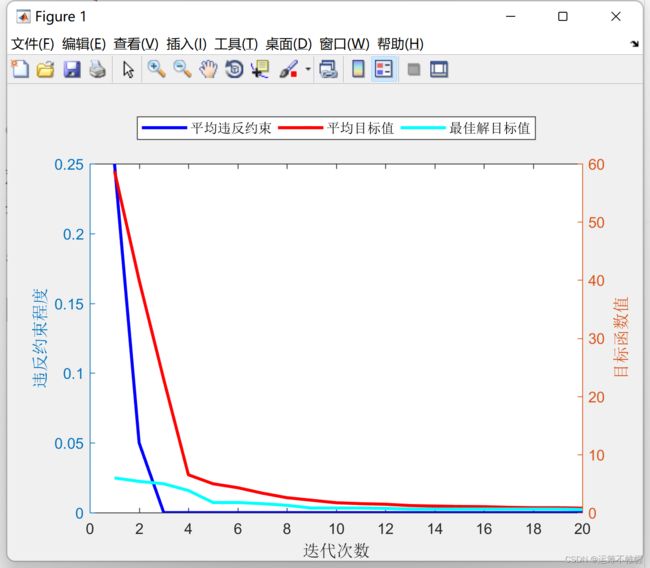
算法稳定收敛。最后是程序文件夹。具体代码可以点开我CSDN空间进行下载。或者私信、留言邮箱。
本次使用的例子非常简单,下期将介绍实战。随机从里面挑选问题进行分析,有兴趣的可以关注一下。
最后,博主专注于论文的复现工作,有兴趣的同学可以私信共同探讨。相关代码已经上传到资源共享,点击我的空间查看分享代码。