改进的粒子群算法(PSO)算法Python代码——非对称学习因子

前三篇链接：

1. 使用基础粒子群(PSO)算法求解一元及二元方程的Python代码
2. 改进的粒子群算法(PSO)算法Python代码——线性/非线性递减惯性权重
3. 改进的粒子群算法(PSO)算法Python代码——随机惯性权重

基本的速度更新公式为：

$$v_i^d=w{v}_i^{d-1}+c_1{r}_1(pbes{t}_i^d-x_i^d)+c_2{r}_2(gbes{t}^d-x_i^d)$$
其中，下标$i$表示第i个粒子，上标$d$表示第d次循环，$v_i^d$表示第i个粒子第d次循环的速度，$w$为惯性权重，$c_1,c_2$分别表示个体学习因子和社会学习因子，一般取2，$pbes{t}_i^d$表示第i个粒子在前d-1次循环中出现的最佳位置，$gbes{t}^d$表示所有粒子在前d-1次循环中出现的最佳位置，$r_1,r_2$分别是两个位于$[0,1]$的随机数。

非对称学习因子

学习因子$c_1,c_2$决定粒子个体经验信息和其他粒子经验信息对寻优轨迹的影响，反映了粒子之间的信息交换。设置较大的$c_1$值，会使粒子过多的在局部搜索；反之，较大的$c_2$值，会使粒子过早收敛到局部最优值。因此，在算法搜索初期采用较大的$c_1$值和较小的$c_2$值，使粒子尽量发散到搜索空间，即强调“个体独立意识”，而较少受到种群内其他粒子，即“社会意识部分”的影响，以增加群内粒子的多样性。

随着迭代次数的增加，使$c_1$线性递减，$c_2$线性递增，从而加强了粒子向全局最优点的收敛能力。

$c_1,c_2$的更新公式如下：

$$c_1=c_{1i}+k\times (c_{1f}-c_{1i})/k_{max}$$
$$c_2=c_{2i}+k\times (c_{2f}-c_{2i})/k_{max}$$
其中，$k$为当前迭代的次数，$k_{max}$是最大迭代数，$c_{1i},c_{2i}$分别是$c_1,c_2$初值，$c_{1f},c_{2f}$分别是$c_1,c_2$终值。
当$c_{1i}\ne c_{2f}$且$c_{2i}\ne c_{1f}$时，即为非对称学习因子方法。

例子

1. 题目
   求函数$y=x_1^2+x_2^2-x_1{x}_2-10x_1-4x_2+60$在$x_1,x_2\in [-15,15]$内的最小值。
2. 流程图
   
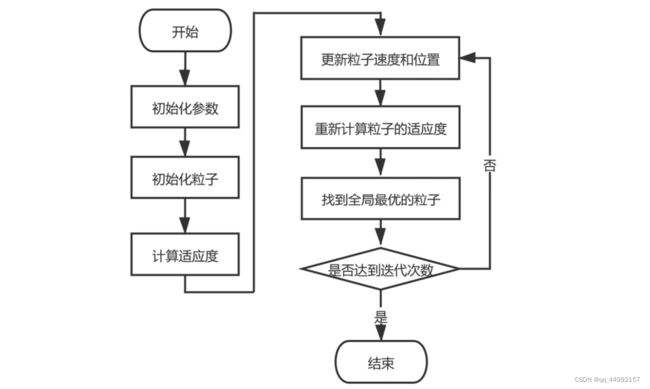
3. 学习因子范围：
   $c_{1i}=2.5,c_{1f}=0.5;c_{2i}=1,c_{2f}=2.25$
4. Python代码：

# 第一步，绘制函数图像
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d

def func(x,y):
    return x**2+y**2-x*y-10*x-4*y+60

x0 = np.linspace(-15,15,100)
y0 = np.linspace(-15,15,100)
x0,y0 = np.meshgrid(x0,y0)
z0 = func(x0,y0)
fig = plt.figure(constrained_layout=True)
ax = fig.add_subplot(projection='3d')
ax.plot_surface(x0,y0,z0,cmap=plt.cm.viridis,alpha=0.7)
ax.set_title('$y = x_1^2+x_2^2-x_1x_2-10x_1-4x_2+60$')

# 第二步，设置粒子群算法的参数
n = 30 # 粒子数量
narvs = 2 # 变量个数
c1i = 2.5 # 个体学习因子初值
c1f = 0.5 # 个体学习因子终值
c2i = 1 # 社会学习因子初值
c2f = 2.25 # 社会学习因子初值
w = 0.9 # 惯性权重
K = 40 # 迭代次数
vxmax = np.array([(15-(-15))*0.2,(15-(-15))*0.2]) # 粒子在x方向的最大速度
x_lb = np.array([-15,-15]) # x和y的下界
x_ub = np.array([15,15]) # x和y的上界

# 第三步，初始化粒子   
x = x_lb + (x_ub-x_lb)*np.random.rand(n,narvs)
v = -vxmax + 2*vxmax*np.random.rand(n,narvs)

# 第四步，计算适应度
fit = func(x[:,0],x[:,1]) # 计算每个粒子的适应度
pbest = x # 初始化这n个例子迄今为止找到的最佳位置
ind = np.argmax(fit) # 找到适应度最大的那个粒子的下标
gbest = x[ind,:]
gbest_total = np.zeros(K)

# 第五步，更新粒子速度和位置
for j in range(K): # 外层循环，共K次
    c1 = c1i + j*(c1f-c1i)/K # 计算j次循环时，个体学习因子的值
    c2 = c2i + j*(c2f-c2i)/K # 计算j次循环时，社会学习因子的值
    for p in range(n):
        v[p,:] = w*v[p,:] + c1*np.random.rand(narvs)*(pbest[p,:]-x[p,:]) + c2*np.random.rand(narvs)*(gbest-x[p,:])
    loc_v = np.where(v<-vxmax)
    v[loc_v] = -vxmax[loc_v[1]] # 速度小于-vmax的元素赋值为-vmax
    loc_v = np.where(v>vxmax)
    v[loc_v] = vxmax[loc_v[1]] # 速度大于vmax的元素赋值为vmax
    x = x + v # 更新第i个粒子的位置
    loc_x = np.where(x<x_lb)
    x[loc_x] = x_lb[loc_x[1]]
    loc_x = np.where(x>x_ub)
    x[loc_x] = x_ub[loc_x[1]]
    
    # 第六步，重新计算适应度并找到最优粒子
    fit = func(x[:,0],x[:,1]) # 重新计算n个粒子的适应度
    for k in range(n): # 更新第k个粒子迄今为止找到的最佳位置
        if fit[k]<func(pbest[k,0],pbest[k,1]):
            pbest[k,:] = x[k,:]
    if np.min(fit)<func(gbest[0],gbest[1]): # 更新所有粒子迄今找到的最佳位置
        gbest = x[np.argmin(fit),:]
    gbest_total[j] = func(gbest[0],gbest[1])

ax.scatter(x[:,0],x[:,1],fit,c='r',marker='x')
fig,ax = plt.subplots()
ax.plot(np.arange(K),gbest_total)
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来显示负号
ax.set_title('算法找到的最小值随优化次数的变化曲线')
ax.set_xlabel('循环次数')
ax.autoscale(axis='x',tight=True)
print('找到的最优解为：',func(gbest[0],gbest[1]))

5. 绘制结果

• 打印输出最优解：找到的最优解为： 8.00454999083955
  可以看出，比原始算法的精度提高了很多，但精度有限；多次运行可以看到不同的精度。
• 显示最终粒子所在的位置：

其中红色叉号表示最后一次循环结束后粒子所在的位置。可以看出，相比原始算法，粒子更多分布在最优点周围。

• 循环过程中最优解随循环次数的变化曲线：
  
  可以看出，收敛速度明显高于原始算法的速度。
  此外，还可以将惯性权重的线性递减与非线性递减与其融合，可以得到更快的收敛速度和更高的精度。